| Citation: | Hongfang Bai. WEAK N-BEST POAFD FOR SOLVING PARABOLIC EQUATIONS IN REPRODUCING KERNEL HILBERT SPACE[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1650-1671. doi: 10.11948/20220086 |
WEAK N-BEST POAFD FOR SOLVING PARABOLIC EQUATIONS IN REPRODUCING KERNEL HILBERT SPACE
-
Abstract
The analytical solutions and numerical ones of parabolic equations in one space variable and the time variable are constructed by weak N-best pre-orthogonal adaptive Fourier decomposition method (weak N-best POAFD) in reproducing kernel Hilbert space (RKHS). To apply weak N-best POAFD, we first choose a dictionary for weak N-best POAFD and implement pre-orthonormalization to all dictionary elements. Then select some parameters by weak N-best maximal selection principle and determine some normalized dictionary elements iteratively. Thus, the analytical solution can be expressed as a linear combination of these determined normalized dictionary elements with a fast convergence rate. Some numerical examples confirm the good accuracy and applicability of the weak N-best POAFD method in solving the partial differential equations.
-

-
References
[1] S. Abbasbandy, R. A. Van Gorder and P. Bakhtiari, Reproducing kernel method for the numerical solution of the Brinkman-Forchheimer momentum equation, J. Comput. Appl. Math., 2017, 311, 262-271. [2] P. Bakhtiari, S. Abbasbandy and R. A. Van Gorder, Reproducing kernel method for the numerical solution of the 1D Swift-Hohenberg equation, Appl. Math. Comput., 2018, 339, 132-143. [3] Q. Chen, T. Qian and L. Tan, A theory on non-constant frequency decompositions and applications, Advancements in Complex Analysis, 2020, DOI:10.1007/978-3-030-40120-7_1. [4] M. Cui and Y. Lin, Nonlinear Numerical Analysis in the Reproducing Kernel Space, Nova Science, New York, 2009. [5] L. Lapidus and G. F. Pinder, Numerical Solution of Partial Differential Equation in Science and Engineering, John Wiley and Sons, Inc., New York, 1999. [6] J. Niu, L. Sun, M. Xu and J. Hou, A reproducing kernel method for solving heat conduction equations with delay, Appl. Math. Lett., 2020, 10, 1-7. [7] M. N. Özisik, H. R. B. Orlande, M. J. Colaço and R. M. Cotta, Finite Difference Methods in Heat Transfer, Taylor and Francis Group, Boca Raton, 2017. [8] T. Qian, Two-dimensional adaptive Fourier decomposition, Math. Meth. Appl. Sci., 2016, 39(10), 2431-2448. doi: 10.1002/mma.3649 [9] T. Qian, A novel Fourier theory on non-linear phases and applications, Advances in Mathematics (CHINA), 2018, 47(3), 321-347. (in Chinese). [10] T. Qian, I. T. Ho, I. T. Leong and Y. Wang, Adaptive decomposition of functions into pieces of non-negative instantaneous frequencies, Int. J. Wavelets, Multiresolut, Inf. Process, 2010, 34(8), 813-833. [11] T. Qian and Y. Wang, Adaptive Fourier series-a variation of greedy algorithm, Adv. Comput. Math., 2011, 34(3), 279-293. doi: 10.1007/s10444-010-9153-4 [12] D. Sharma, K. Goyal and R. K. Singla, A curvelet method for numerical solution of partial differential equations, Appl. Numer. Math., 2020, 148, 28-44. doi: 10.1016/j.apnum.2019.08.029 [13] D. Watson, Radial Basis Function Differential Quadrature Method for the Numerical Solution of Partial Differential Equations, Dissertation, 2017. https://aquila.usm.edu/dissertations/1468. [14] Z. Weng, S. Zhai, Y. Zeng and X. Yue, Numerical approximation of the elliptic eigenvalue problem by stablized nonconforming finite element element method, J. Appl. Anal. Comput., 2021, 11(3), 1161-1176. -
-
-
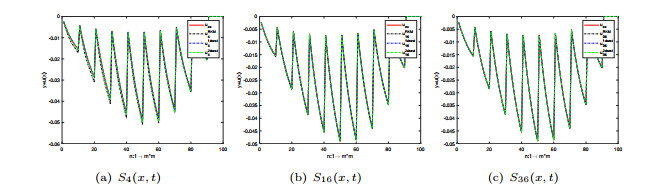
Figure 1. The numerical solutions
$ S_4(x, t) $ ,$ S_{16}(x, t) $ ,$ S_{36} $ obtained by RKM in [4], weak 1-best POAFD and weak 2-best POAFD for Example 4.1, respectively. -
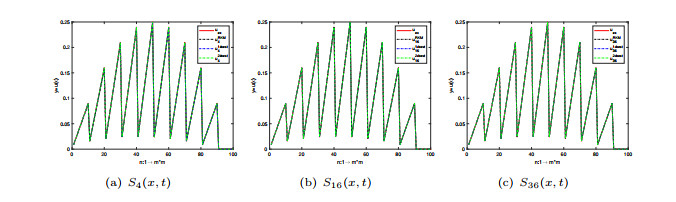
Figure 2. The numerical solutions
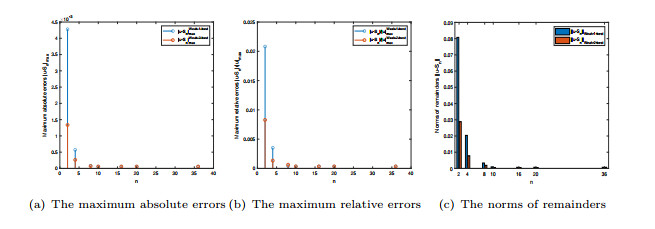
$ S_4(x, t) $ ,$ S_{16}(x, t) $ ,$ S_{36} $ obtained by RKM in [4], weak 1-best POAFD and weak 2-best POAFD for Example 4.2, respectively. - Figure 3. Comparison of numerical results for Example 4.1.
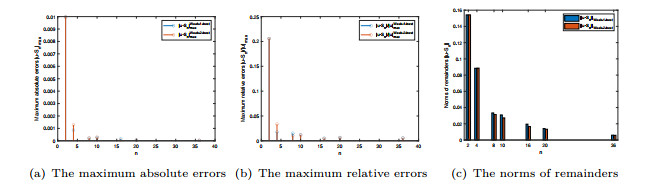
- Figure 4. Comparison of numerical results for Example 4.2.




 DownLoad:
DownLoad: