| Citation: |
Mamta Kapoor. SUMUDU TRANSFORM FOR TIME FRACTIONAL PHYSICAL MODELS AN ANALYTICAL ASPECT[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1255-1273. doi: 10.11948/20220096
|
SUMUDU TRANSFORM FOR TIME FRACTIONAL PHYSICAL MODELS AN ANALYTICAL ASPECT
-
Abstract
Present paper deals with the development of a novel and reliable algorithm to solve various time-fractional differential prototypes regarding engineering and physics. The developed algorithm is named as Sumudu Iterative Transform Regime. In present work, proposed regime is applied to tackle different models of importance. The fetched results have shown the efficiency, efficacy and reliability of the developed scheme. In most of the cases, closed form of the solutions is provided. Moreover, profiles of solutions are provided to show the behavior of the fetched results. Error analysis of the results is already notified as well as convergence aspect is also mentioned. On the basis of the discussed aspects, it can be claimed the Sumudu Iterative Transform Regime is a robust technique to deal with the complex natured PDEs. Present scheme will surely add importance in the literature. With the aid of the present regime numerous fractional PDEs and partial-integro differential equations can be tackled.
-
-
References
[1] Z. Ahmeda, M. I. Idreesb, F. B. M. Belgacemc and Z. Perveen, On the convergence of double sumudu transform, Journals of Nonlinear Sciences and Applications, 2019, 13, 154–162. doi: 10.22436/jnsa.013.03.04 [2] L. Akinyemi and O. S. Iyiola, Exact and approximate solutions of time-fractional models arising from physics via Shehu transform, Mathematical Methods in the Applied Sciences, 2020, 43(12), 7442–7464. doi: 10.1002/mma.6484 [3] L. Akinyemi and O. S. Iyiola, Analytical study of (3+1)-dimensional fractional-reaction diffusion trimolecular models, International Journal of Applied and Computational Mathematics, 2021, 7(3), 1–24. [4] A. Atangana and D. Baleanu, Nonlinear fractional Jaulent-Miodek and Whitham-Broer-Kaup equations within Sumudu transform, in Abstract and applied analysis, 2013, Hindawi, 2013. [5] S. Cetinkaya, A. Demir and H. K. Sevindir, Solution of space-time-fractional problem by Shehu variational iteration method, Advances in Mathematical Physics, 2021, 2021. [6] G. H. Hardy, Gösta Mittag-Leffler, 1846–1927, Proc. R. Soc. Lond. (A), 1928, 119. [7] O. S. Iyiola, E. Asante-Asamani and B. A. Wade, A real distinct poles rational approximation of generalized Mittag-Leffler functions and their inverses: applications to fractional calculus, Journal of Computational and Applied Mathematics, 2018, 330, 307–317. [8] A. C. Loyinmi and T. K. Akinfe, Exact solutions to the family of fisher's reaction-diffusion equation using Elzaki homotopy transformation perturbation method, Engineering Reports, 2020, 2(2), e12084. [9] Y. Luchko and R. Gorenflo, An operational method for solving fractional differential equations with the Caputo derivatives, Acta Math. Vietnam, 1999, 24(2), 207–233. [10] F. Mainardi, On the initial value problem for the fractional diffusion-wave equation, Waves and Stability in Continuous Media, World Scientific, Singapore, 1994, 1994, 246–251. [11] F. Mainardi, The fundamental solutions for the fractional diffusion-wave equation, Applied Mathematics Letters, 1996, 9(6), 23–28. doi: 10.1016/0893-9659(96)00089-4 [12] N. S. Malagi, P. Veeresha, B. Prasannakumara et al., A new computational technique for the analytic treatment of time-fractional Emden-Fowler equations, Mathematics and Computers in Simulation, 2021, 190, 362–376. doi: 10.1016/j.matcom.2021.05.030 [13] A. Prakash, V. Verma, D. Kumar and J. Singh, Analytic study for fractional coupled Burger's equations via Sumudu transform method, Nonlinear Engineering, 2018, 7(4), 323–332. doi: 10.1515/nleng-2017-0090 [14] D. Prakasha, P. Veeresha and J. Singh, Fractional approach for equation describing the water transport in unsaturated porous media with Mittag-Leffler kernel, Frontiers in Physics, 2019, 7, 193. doi: 10.3389/fphy.2019.00193 [15] D. G. Prakasha, N. S. Malagi and P. Veeresha, New approach for fractional Schrödinger-Boussinesq equations with Mittag-Leffler kernel, Mathematical Methods in the Applied Sciences, 2020, 43(17), 9654–9670. doi: 10.1002/mma.6635 [16] D. G. Prakasha, N. S. Malagi, P. Veeresha and B. C. Prasannakumara, An efficient computational technique for time-fractional Kaup-Kupershmidt equation, Numerical Methods for Partial Differential Equations, 2021, 37(2), 1299–1316. doi: 10.1002/num.22580 [17] S. Saha Ray, A novel method for travelling wave solutions of fractional Whitham-Broer-Kaup, fractional modified Boussinesq and fractional approximate long wave equations in shallow water, Mathematical Methods in the Applied Sciences, 2015, 38(7), 1352–1368. doi: 10.1002/mma.3151 [18] N. A. Shah and J. D. Chung, The analytical solution of fractional-order Whitham-Broer-Kaup equations by an Elzaki decomposition method, Numerical Methods for Partial Differential Equations, 2021. [19] A. Shukla and J. Prajapati, On a generalization of Mittag-Leffler function and its properties, Journal of mathematical analysis and applications, 2007, 336(2), 797–811. doi: 10.1016/j.jmaa.2007.03.018 [20] P. Veeresha, N. S. Malagi, D. Prakasha and H. M. Baskonus, An efficient technique to analyze the fractional model of vector-borne diseases, Physica Scripta, 2022, 97(5), 054004. doi: 10.1088/1402-4896/ac607b [21] P. Veeresha, D. Prakasha, M. Qurashi and D. Baleanu, A reliable technique for fractional modified Boussinesq and approximate long wave equations, Advances in Difference Equations, 2019, 2019(1), 1–23. doi: 10.1186/s13662-018-1939-6 [22] P. Veeresha, D. G. Prakasha, H. M. Baskonus and G. Yel, An efficient analytical approach for fractional Lakshmanan-Porsezian-Daniel model, Mathematical Methods in the Applied Sciences, 2020, 43(7), 4136–4155. [23] G. Watugala, Sumudu transform: a new integral transform to solve differential equations and control engineering problems, Integrated Education, 1993, 24(1), 35–43. -
-
Figures(6) / Tables(3)
Export File
Citation
Mamta Kapoor. SUMUDU TRANSFORM FOR TIME FRACTIONAL PHYSICAL MODELS AN ANALYTICAL ASPECT[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1255-1273. doi: 10.11948/20220096
Format
Content
DownLoad:
-
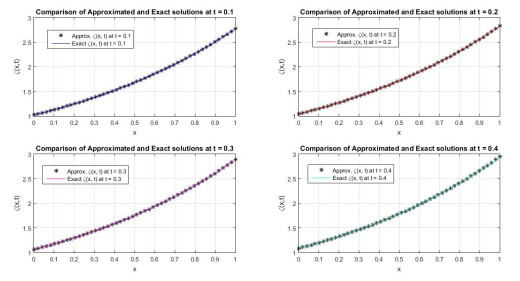
Figure 1.
Approx. and exact results at
$ t= 0.1, 0.2, 0.3 $ $ 0.4 $ $ \epsilon_1=\epsilon_2=\epsilon_3=0.1 $ $ \mu=1 $ $ N=50 $ -
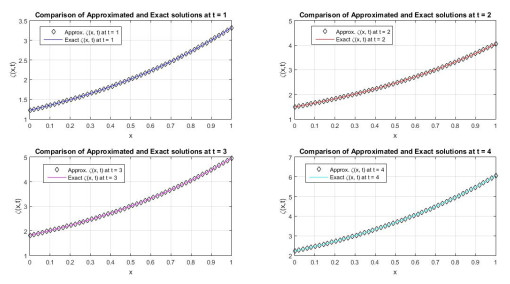
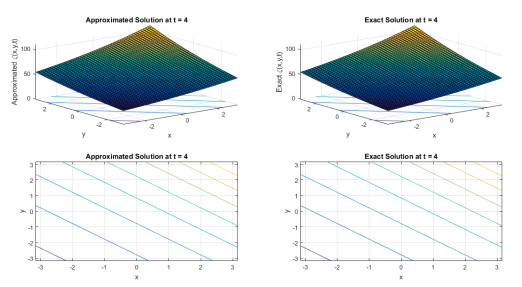
Figure 2.
Approx. and exact results at
$ t= 1, 2, 3 $ $ 4 $ $ \epsilon_1=\epsilon_2=\epsilon_3=0.1 $ $ \mu=1 $ $ N=50 $ -
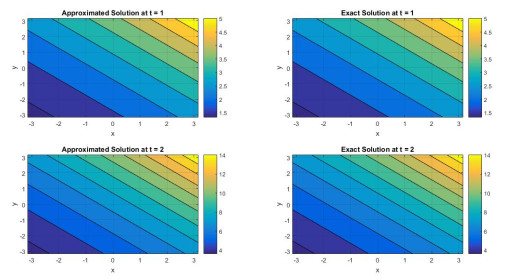
Figure 3.
2D plot for Approx. and Exact results at
$ t $ $ \mu $ $ \gamma $ $ N $ -
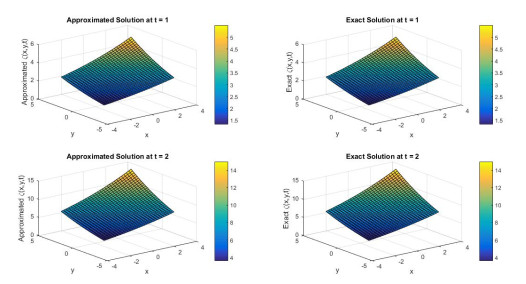
Figure 4.
3D plot for Approx. and Exact results at
$ t $ $ \mu $ $ \gamma $ $ N $ -
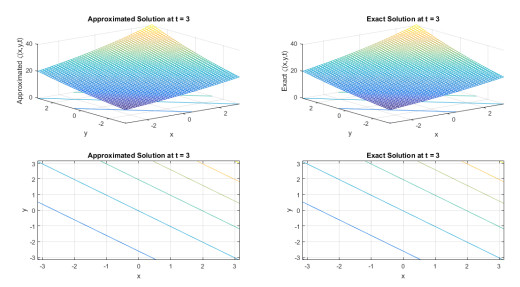
Figure 5.
Mesh and contour plot for approx. and exact solution profiles at
$ t $ $ N $ -
Figure 6.
Surface and contour plot for approx. and exact solution profiles at
$ t $ $ N $