| Citation: |
Xia Liu. THE NUMBER OF LIMIT CYCLES FROM ELLIPTIC HAMILTONIAN VECTOR FIELDS BY HIGHER ORDER MELNIKOV FUNCTIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1239-1254. doi: 10.11948/20220063
|
THE NUMBER OF LIMIT CYCLES FROM ELLIPTIC HAMILTONIAN VECTOR FIELDS BY HIGHER ORDER MELNIKOV FUNCTIONS
-
Abstract
In this paper, the perturbed Hamiltonian system $ dH=\epsilon F_4+\epsilon^2F_3+\epsilon^3F_2+\epsilon^4F_1 $, with $ F_i $ the vector valued homogeneous polynomials of degree $ i $. The Hamiltonian function is $ H=y^2/2+U(X), $ where $ U $ is a univariate polynomial of degree four without symmetry. By computing higher order Melnikov functions, the upper bounds for the number of limit cycles that bifurcate from $ dH=0 $ are deserved.
-
Keywords:
- Melnikov functions /
- bifurcation /
- limit cycles /
- generators
-
-
References
[1] R. Asheghi and A. Nabavi, Higher order Melnikov functions for studying limit cycles of some perturbed elliptic Hamiltonian vector fields, Qual. Theory Dyn. Syst., 2019, 18, 289–313. doi: 10.1007/s12346-018-0284-1 [2] R. Asheghi and A. Nabavi, The third order melnikov function of a cubic integrable system under quadratic perturbations, Chaos, Solitons and Fractals, 2020, 139, 110291. doi: 10.1016/j.chaos.2020.110291 [3] A. Buica, A. Gasull and J. Yang, The third order Melnikov function of a quadratic center under quadratic perturbations, J. Math. Anal. Appl., 2007, 331, 443–454. doi: 10.1016/j.jmaa.2006.09.008 [4] J. P. Françoise, Successive derivatives of a first return map, application to the study of quadratic vector fields, Ergodic Theory Dynam. Systems, 1996, 16, 87–96. doi: 10.1017/S0143385700008725 [5] J. P. Françoise, H. He and D. Xiao, The number of limit cycles bifurcating from the period annulus of quasi-homogeneous Hamiltonian systems at any order, Journal of Differential Equations, 2021, 276, 318–341. doi: 10.1016/j.jde.2020.12.015 [6] M. Gentes, Center conditions and limit cycles for the perturbation of an elliptic sector, Bull. Sci. Math., 2009, 133, 597–643. doi: 10.1016/j.bulsci.2009.04.002 [7] L. Gavrilova and I. D. Iliev, Cubic perturbations of elliptic Hamiltonian vector fields of degree three, J. Differential Equations, 2016, 260, 3963–3990. doi: 10.1016/j.jde.2015.10.052 [8] L. Gavrilov, et al., Special cubic perturbations of the Duffing oscillator $x''= x - x^3$ near the eight-Loop, Mediterr. J. Math., 2021, 18, 229. doi: 10.1007/s00009-021-01868-5 [9] B. B. Hamed, et al., Cubic perturbations of symmetric elliptic Hamiltonians of degree four in a complex domain, Bull. Sci. math., 2019, 157, 102796. doi: 10.1016/j.bulsci.2019.102796 [10] M. Han and J. Chen, The number of limit cycles bifurcating from a pair of homoclinic loops, Sci. China, 2000, 30A, 401–414. [11] M. Han and C. Fan, On the number and distributions of limit cycles in a quartic system, Chin. Ann. Math., 2005, 26A, 825–834. [12] M. Han and J. Yang, The maximum number of zeros of functions with parameters and application to differential equations, Journal of Nonlinear Modeling and Analysis, 2021, 3, 13–34. [13] I. D. Iliev, On second order bifurcations of limit cycles, J. London Math. Soc., 1998, 58, 353–366. doi: 10.1112/S0024610798006486 [14] I. D. Iliev, The number of limit cycles due to polynomial perturbations of the harmonic oscillator, Math. Proc. Cambridge Philos. Soc., 1999, 127, 317–322. doi: 10.1017/S0305004199003795 [15] I. D. Iliev, On the limit cycles available from polynomial perturbations of the Bogdanov-Takens Hamiltonian, Israel Journal of Mathematics, 2000, 115, 269–284. doi: 10.1007/BF02810590 [16] S. Liu, X. Jin and Y. Xiong, The number of limit cycles in a class of piecewise polynomial systems, Journal of Nonlinear Modeling and Analysis, 2022, 4, 352–370. [17] X. Sun and P. Yu, Cyclicity of periodic annulus and Hopf cyclicity in perturbing a hyper-elliptic Hamiltonian system with a degenerate heteroclinic loop, J. Differential Equations, 2020, 269, 9224–9253. doi: 10.1016/j.jde.2020.06.037 [18] Y. Tian and M. Han, Hopf and homoclinic bifurcations for near-Hamiltonian systems, J. Differential Equations, 2017, 262, 3214–3234. doi: 10.1016/j.jde.2016.11.026 [19] G. Tigan, Using Melnikov functions of any order for studying limit cycles, J. Math. Anal. Appl., 2017, 448, 409–420. doi: 10.1016/j.jmaa.2016.11.021 [20] J. Yang and M. Han, Limit cycles near a double homoclinic loop, Ann. of Diff. Eqs., 2007, 23, 536–545. [21] J. Yang, M. Han and V. G. Romanovski, Limit cycle bifurcations of some Lienard systems, J. Math. Anal. Appl., 2010, 366, 242–255. doi: 10.1016/j.jmaa.2009.12.035 [22] P. Yang and J. Yu, The number of limit cycles from a cubic center by the Melnikov function of any order, J. Differential Equations, 2020, 268, 1463–1494. doi: 10.1016/j.jde.2019.08.053 [23] Y. Zhao and Z. Zhang, Linear estimate of the number of zeros of Abelian integrals for a kind of quartic Hamiltonians, J. Differential Equations, 1999, 155, 73–88. doi: 10.1006/jdeq.1998.3581 -
-
Figures(1)
Export File
Citation
Xia Liu. THE NUMBER OF LIMIT CYCLES FROM ELLIPTIC HAMILTONIAN VECTOR FIELDS BY HIGHER ORDER MELNIKOV FUNCTIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1239-1254. doi: 10.11948/20220063
Format
Content
DownLoad:
-
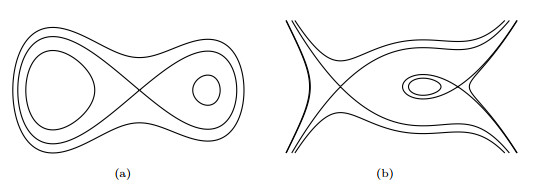
Figure 1.
(a)
$ \frac{8}{9}<a<1 $ $ a<0 $