| Citation: |
Yongkun Li, Xiaoli Huang. WEYL ALMOST PERIODIC FUNCTIONS ON TIME SCALES AND WEYL ALMOST PERIODIC SOLUTIONS OF DYNAMIC EQUATIONS WITH DELAYS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1022-1042. doi: 10.11948/20220102
|
WEYL ALMOST PERIODIC FUNCTIONS ON TIME SCALES AND WEYL ALMOST PERIODIC SOLUTIONS OF DYNAMIC EQUATIONS WITH DELAYS
-
Abstract
Due to the incompleteness of the space composed of Weyl almost periodic functions, there are few results on the existence of Weyl almost periodic solutions of differential equations. In addition, as a discrete analogs of differential equations, there is almost no result of the existence of Weyl almost periodic solutions of difference equations. Because dynamic equations on time scales can unify the study of differential equations and difference equations. Therefore, in this paper, we first propose a concept of Weyl almost periodic functions on time scales. Then, taking a Clifford-valued neural network with time-varying delays on time scales as an example of dynamic equations on time scales, we study the existence and stability of Weyl almost periodic solutions of this neural network on time scales. Even when the system we consider degenerates into a real-valued system, our results are new. A numerical example is given to illustrate the feasibility of our results.
-
-
References
[1] J. Ao and N. Liu, Third order boundary value problem with finite spectrum on time scales, J. Appl. Anal. Comput., 2020, 10(5), 1869-1877. [2] C. Aouiti and F. Dridi, Weighted pseudo almost automorphic solutions for neutral type fuzzy cellular neural networks with mixed delays and D operator in Clifford algebra, Int. J. Syst. Sci., 2020, 51(10), 1759-1781. doi: 10.1080/00207721.2020.1777345 [3] C. Aouiti and I. B. Gharbia, Dynamics behavior for second-order neutral Clifford differential equations: inertial neural networks with mixed delays, Comput. Appl. Math., 2020. DOI: 10.1007/s40314-020-01148-0. [4] C. Aouiti, I. B. Gharbia, J. Cao and X. Li, Asymptotic behavior of Clifford-valued dynamic systems with D-operator on time scales, Adv. Differ. Equ., 2021. DOI: 10.1186/s13662-021-03266-3. [5] A. S. Besicovitch, Almost Periodic Functions, Dover, New York, 1954. [6] M. Bohner and G. S. Guseinov, Double integral calculus of variations on time scales, Comput. Math. Appl., 2007, 54(1), 45-57. doi: 10.1016/j.camwa.2006.10.032 [7] M. Bohner and A. Peterson, Dynamic Equations on Time Scales, An Introduction with Applications, Birkhäuser, Boston, 2001. [8] H. Bohr, Zur Theorie der fastperiodischen Funktionen, I, Acta Math., 1925, 45, 29-127. doi: 10.1007/BF02395468 [9] H. Bohr, Zur Theorie der fastperiodischen Funktionen, II, Acta Math., 1925 46, 101-214. doi: 10.1007/BF02543859 [10] S. Buchholz, A theory of neural computation with Clifford algebras, Ph. D. thesis, University of Kiel, 2005. [11] A. Cabada and D. R. Vivero, Expression of the Lebesgue $\Delta$-integral on time scales as a usual Lebesgue integral; application to the calculus of $\Delta$-antiderivatives, Math. Comput. Modelling, 2006, 43, 194-207. doi: 10.1016/j.mcm.2005.09.028 [12] A. Chaouki and F. Touati, Global dissipativity of Clifford-valued multidirectional associative memory neural networks with mixed delays, Comput. Appl. Math., 2020. DOI: 10.1007/s40314-020-01367-5. [13] C. Corduneanu, Almost periodic oscillations and waves, Springer, New York, 2009. [14] B. Du, Y. Liu, H. A. Batarfi and F. E. Alsaadi, Almost periodic solution for a neutral-type neural networks with distributed leakage delays on time scales, Neurocomputing, 2016, 173, 921-929. doi: 10.1016/j.neucom.2015.08.047 [15] M. Es-saiydy and M. Zitane, Weighted Stepanov-like pseudo almost periodicity on time scales and applications, Differ. Equ. Dyn. Syst., 2020. In press, DOI: 10.1007/s12591-020-00543-7. [16] J. Gao, Q. Wang and L. Zhang, Existence and stability of almost-periodic solutions for cellular neural networks with time-varying delays in leakage terms on time scales, Appl. Math. Comput., 2014, 237, 639-649. [17] S. Hilger, Analysis on measure chains-a unified approach to continuous and discrete calculus, Result Math., 1990, 18(1-2), 18-56. doi: 10.1007/BF03323153 [18] E. Hitzer, T. Nitta and Y. Kuroe, Applications of Clifford's geomeric algebra, Adv. Appl. Clifford Algebras, 2013, 23(2), 377-404. doi: 10.1007/s00006-013-0378-4 [19] S. Hong and Y. Peng, Almost periodicity of set-valued functions and set dynamic equations on time scales, Inform. Sci., 2016, 330, 157-174. doi: 10.1016/j.ins.2015.10.008 [20] S. Huang, Y. Qiao and G. Wen, Real and Complex Clifford Analysis, Springer, New York, 2006. [21] Q. Jiang and Q. Wang, Almost periodic solutions for quaternion-valued neural networks with mixed delays on time scales, Neurocomputing, 2021, 439, 363-373. doi: 10.1016/j.neucom.2020.09.063 [22] M. Kéré, G. M. Guérékata and E. R. Oueama, An existence result of $\mu $-pseudo almost automorphic solutions of Clifford-valued semi-linear delay differential equations, Malaya J. Mat., 2021, 9(3), 129-140. [23] B. M. Levitan and V. V. Zhikov, Almost Periodic Functions and Differential Equations, Cambridge Univ. Press, London, 1982. [24] Y. Li, Almost periodic functions on the quantum time scale and applications, Discrete Dynamics in Nature and Society, 2019. DOI: 10.1155/2019/4529159. [25] Y. Li and B. Li, Pseudo compact almost automorphy of neutral type Clifford-valued neural networks with mixed delays, Discrete Contin. Dyn. Syst. B, 2021, in press, doi: 10.3934/dcdsb.2021248. [26] Y. Li and S. Shen, Compact almost automorphic function on time scales and its application, Qual. Theory Dynam. Syst., 2021. DOI: 10.1007/s12346-021-00522-5. [27] Y. Li and C. Wang, Uniformly almost periodic functions and almost periodic solutions to dynamic equations on time scales, Abstract and Applied Analysis, 2011. DOI: 10.1155/2011/341520. [28] Y. Li and C. Wang, Pseudo almost periodic functions and pseudo almost periodic solutions to dynamic equations on time scales, Adv. Differ. Equ., 2012. DOI: 10.1186/1687-1847-2012-77. [29] Y. Li and P. Wang, Almost periodic solution for neutral functional dynamic equations with Stepanov-almost periodic terms on time scales, Discrete Contin. Dyn. Syst. S, 2017, 10(3), 463-473. doi: 10.3934/dcdss.2017022 [30] Y. Li, X. Wang and N. Huo, Weyl almost automorphic solutions in distribution sense of Clifford-valued stochastic neural networks with time-varying delays, Proceedings of the Royal Society A, 2022, 478(2257), 20210719. DOI: 10.1098/rspa.2021.0719. [31] H. Liu, Half-linear Volterra-Fredholm type integral inequalities on time scales and their applications, J. Appl. Anal. Comput., 2020, 10(1), 234-248. [32] Y. Liu, P. Xu, J. Lu and J. Liang, Global stability of Clifford-valued recurrent neural networks with time delays, Nonlinear Dyn., 2016, 84(2), 767-777. doi: 10.1007/s11071-015-2526-y [33] C. Lizama, J. G. Mesquita and R. Ponce, A connection between almost periodic functions defined on timescales and $\mathbb{R}$, Applic. Anal., 2014, 93(12), 2547-2558. doi: 10.1080/00036811.2013.875161 [34] G. Rajchakit, R. Sriraman, N. Boonsatit, P. Hammachukiattikul, C. P. Lim and P. Agarwal, Global exponential stability of Clifford-valued neural networks with time-varying delays and impulsive effects, Adv. Differ. Equ., 2021. DOI: 10.1186/s13662-021-03367-z. [35] G. Rajchakit, R. Sriraman, P. Vignesh and C. P. Lim, Impulsive effects on Clifford-valued neural networks with time-varying delays: An asymptotic stability analysis, Appl. Math. Comput., 2021. DOI: 10.1016/j.amc.2021.126309. [36] V. V. Stepanov, Sur quelques généralisations des fonctions presque périodiques, C. R. Acad. Sci. Paris, 1925, 181, 90-92. [37] C. Tang and H. Li, Stepanov-like pseudo almost periodic functions on time scales and applications to dynamic equations with delay, Open Math., 2018, 16(1), 826-841. doi: 10.1515/math-2018-0073 [38] C. Tang and H. Li, Bochner-like transform and Stepanov almost periodicity on time scales with applications, Symmetry, 2018. DOI: 10.3390/sym10110566. [39] H. Weyl, Integralgleichungen und fastperiodische Funktionen, Math. Ann., 1926, 97, 338-356. [40] C. Xu, P. Li and Y. Pang, Existence and global exponential stability of almost periodic solutions for BAM neural networks with distributed leakage delays on time scales, J. Appl. Anal. Comput., 2017, 7(4), 1200-1232. [41] Z. Yan and X. Jia, Stepanov-like pseudo almost periodic solutions for impulsive perturbed partial stochastic differential equations and its optimal control, J. Appl. Anal. Comput., 2020, 10(2), 530-568. [42] Z. Yao, Existence and exponential stability of unique almost periodic solution for Lasota-Wazewska red blood cell model with perturbation on time scales, Math. Meth. Appl. Sci., 2017, 40(13), 4709-4715. [43] X. Yu and Q. Wang, Weighted pseudo-almost periodic solutions for shunting inhibitory cellular neural networks on time scales, Bull. Malays. Math. Sci. Soc., 2019, 42(5), 2055-2074. doi: 10.1007/s40840-017-0595-4 -
-
Figures(6)
Export File
Citation
Yongkun Li, Xiaoli Huang. WEYL ALMOST PERIODIC FUNCTIONS ON TIME SCALES AND WEYL ALMOST PERIODIC SOLUTIONS OF DYNAMIC EQUATIONS WITH DELAYS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1022-1042. doi: 10.11948/20220102
Format
Content
DownLoad:
-
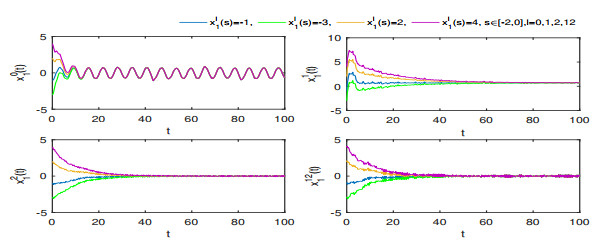
Figure 1.
$ \mathbb{T}=\mathbb{R} $ , states$ x^l_1(t) $ and$ x^l_2(t) $ of system (1.1) with different initial values. -
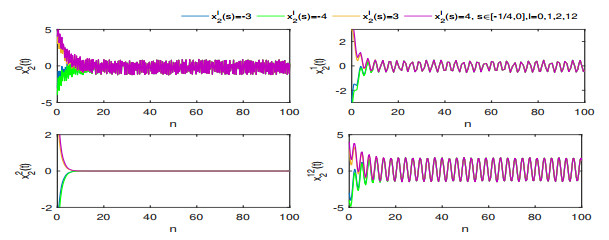
Figure 2.
$ \mathbb{T}=\mathbb{Z} $ , states$ x^l_1(t) $ and$ x^l_2(t) $ of system (1.1) with different initial values. -
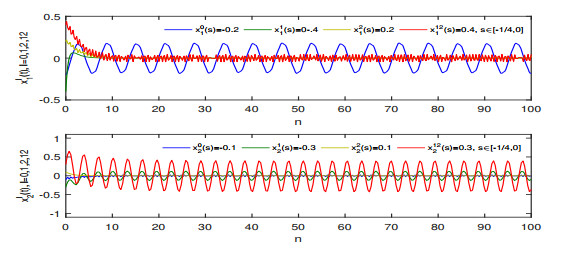
Figure 3.
$ \mathbb{T}=\mathbb{R} $ , the global exponential stability of states$ x_1^0(t), x_1^1(t), x_1^2(t) $ and$ x_1^{12}(t) $ of system (1.1) with different initial values. -
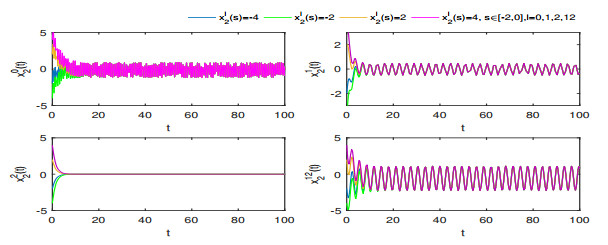
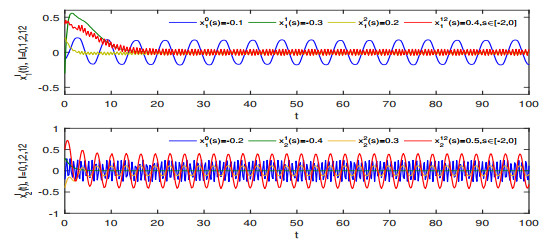
Figure 4.
$ \mathbb{T}=\mathbb{R} $ , the global exponential stability of states$ x_2^0(t), x_2^1(t), x_2^2(t) $ and$ x_2^{12}(t) $ of system (1.1) with different initial values. -
Figure 5.
$ \mathbb{T}=\mathbb{Z} $ , the global exponential stability of states$ x_1^0(t), x_1^1(t), x_1^2(t) $ and$ x_1^{12}(t) $ of system (1.1) with different initial values. -
Figure 6.
$ \mathbb{T}=\mathbb{Z} $ , the global exponential stability of states$ x_2^0(t), x_2^1(t), x_2^2(t) $ and$ x_2^{12}(t) $ of system (1.1) with different initial values.