| Citation: |
H. Dehestani, Y. Ordokhani. IMPROVEMENT OF THE SPECTRAL METHOD FOR SOLVING MULTI-TERM TIME-SPACE RIESZ-CAPUTO FRACTIONAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2600-2620. doi: 10.11948/20220146
|
IMPROVEMENT OF THE SPECTRAL METHOD FOR SOLVING MULTI-TERM TIME-SPACE RIESZ-CAPUTO FRACTIONAL DIFFERENTIAL EQUATIONS
-
Abstract
In this paper, we study the numerical solution of multi-term time-space Riesz-Caputo fractional differential equations with the help of shifted Vieta-Lucas polynomials. To get the desired purpose, we introduce a new method for obtaining the operational matrices. The constructed method for finding the matrices influence directly in the accuracy of the methodology. Thus, the combination of shifted Vieta-Lucas polynomials properties with the operational matrices has reduced the problem to a system of algebraic equations. The proposed approach provides the approximate solutions to the problem which are convergent to the exact solution. Finally, we represent the accuracy and efficiency of the methodology by examining some examples and presenting the results in the form of graphs and tables.
-
-
References
[1] A. Abdon and B. Dumitru, New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model, Therm. Sci., 2016, 20(2), 763-769. doi: 10.2298/TSCI160111018A [2] P. Agarwal and A. El-Sayed, Vieta-Lucas polynomials for solving a fractional-order mathematical physics model, Adv. Differ. Equ., 2020, 2020(1), 1-18. doi: 10.1186/s13662-019-2438-0 [3] A. H. Bhrawy and M. A. Zaky, A method based on the Jacobi Tau approximation for solving multi-term time-space fractional partial differential equations, J. Comput. Phys., 2015, 281, 876-895. doi: 10.1016/j.jcp.2014.10.060 [4] W. Bu, X. Liu, Y. Tang and J. Yang, Finite element multigrid method for multi-term time fractional advection diffusion equations, Int. J. Model. Simul. Sci. Comput., 2015, 6(01), 1540001. doi: 10.1142/S1793962315400012 [5] C. Canuto, M. Y. Hussaini, A. Quarteroni and T. A. Zang, Spectral Methods: Fundamentals in Single Domains, Springer Science & Business Media, 2007. [6] M. Caputo, Linear models of dissipation whose q is almost frequency independent-Ⅱ, Geophys. J. Int., 1967, 13(5), 529-539. doi: 10.1111/j.1365-246X.1967.tb02303.x [7] S. Chen, X. Jiang, F. Liu and I. Turner, High order unconditionally stable difference schemes for the Riesz space-fractional telegraph equation, J. Comput. Appl. Math., 2015, 278, 119-129. doi: 10.1016/j.cam.2014.09.028 [8] H. Dehestani and Y. Ordokhani, Developing the discretization method for fractal-fractional two-dimensional fredholm-volterra integro-differential equations, Math. Methods Appl. Sci., 2021. [9] H. Dehestani and Y. Ordokhani, Modification of numerical algorithm for space-time fractional partial differential equations including two types of fractional derivatives, Int. J. Comput. Math., 2022, (just-accepted), 1. [10] H. Dehestani, Y. Ordokhani and M. Razzaghi, Fractional-order Legendre-Laguerre functions and their applications in fractional partial differential equations, Appl. Math. Comput., 2018, 336, 433-453. [11] A. Elsaid, The variational iteration method for solving Riesz fractional partial differential equations, Comput. Math. Appl., 2010, 60(7), 1940-1947. doi: 10.1016/j.camwa.2010.07.027 [12] R. Erfanifar, K. Sayevand and H. Esmaeili, On modified two-step iterative method in the fractional sense: some applications in real world phenomena, Int. J. Comput. Math., 2020, 97(10), 2109-2141. doi: 10.1080/00207160.2019.1683547 [13] R. Gorenflo and F. Mainardi, Fractional calculus: integral and differential equations of fractional order, arXiv preprint arXiv: 0805.3823, 2008. [14] R. Gorenflo, F. Mainardi, D. Moretti et al., Discrete random walk models for space-time fractional diffusion, Chem. Phys., 2002, 284(1-2), 521-541. doi: 10.1016/S0301-0104(02)00714-0 [15] R. Gorenflo and A. Vivoli, Fully discrete random walks for space-time fractional diffusion equations, Signal Process., 2003, 83(11), 2411-2420. doi: 10.1016/S0165-1684(03)00193-2 [16] I. Gorial, Numerical methods for fractional reaction-dispersion equation with Riesz space fractional derivative, Eng. Tech. J, 2011, 29(4), 709-715. [17] M. Heydari, Z. Avazzadeh and M. Razzaghi, Vieta-Lucas polynomials for the coupled nonlinear variable-order fractional Ginzburg-Landau equations, Appl. Numer. Math., 2021, 165, 442-458. doi: 10.1016/j.apnum.2021.03.007 [18] R. Metzler and J. Klafter, The random walk's guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep., 2000, 339(1), 1-77. doi: 10.1016/S0370-1573(00)00070-3 [19] I. Podlubny, Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Elsevier, 1998. [20] S. Samko, A. Kilbas and O. Marichev, Fractional integrals and derivatives theory and applications gordon and breach, new york, 1993, ISBN-10: 2881248640, 13, 978-2881248641. [21] K. Sayevand, N. Ghanbari and I. Masti, A robust computational framework for analyzing the Bloch-Torrey equation of fractional order, Comput. Appl. Math., 2021, 40(4), 1-21. [22] K. Sayevand and J. A. T. Machado, A survey on fractional asymptotic expansion method: a forgotten theory, Fract. Calc. Appl. Anal., 2019, 22(5), 1165-1176. doi: 10.1515/fca-2019-0062 [23] K. Sayevand, J. T. Machado and I. Masti, Analysis of dual Bernstein operators in the solution of the fractional convection-diffusion equation arising in underground water pollution, J. Comput. Appl. Math., 2022, 399, 113729. doi: 10.1016/j.cam.2021.113729 [24] X. Si, C. Wang, Y. Shen and L. Zheng, Numerical method to initial-boundary value problems for fractional partial differential equations with time-space variable coefficients, Appl. Math. Model., 2016, 40(7-8), 4397-4411. [25] V. E. Tarasov and G. M. Zaslavsky, Fractional dynamics of systems with long-range interaction, Commun. Nonlinear Sci. Numer. Simul., 2006, 11(8), 885-898. [26] W. Tian, H. Zhou and W. Deng, A class of second order difference approximations for solving space fractional diffusion equations, Math. Comput., 2015, 84(294), 1703-1727. [27] H. Ye, F. Liu, V. Anh and I. Turner, Maximum principle and numerical method for the multi-term time-space riesz-caputo fractional differential equations, Appl. Math. Comput., 2014, 227, 531-540. [28] G. M. Zaslavsky, Chaos, fractional kinetics, and anomalous transport, Phys. Rep., 2002, 371(6), 461-580. [29] H. Zhang and F. Liu, The fundamental solutions of the space, space-time Riesz fractional partial differential equations with periodic conditions, Numer. Math., 2007, 16(2), 181. [30] Y. Zhang and H. Ding, Improved matrix transform method for the Riesz space fractional reaction dispersion equation, J. Comput. Appl. Math., 2014, 260, 266-280. [31] Y. Zhang and H. Ding, Numerical algorithm for the time-caputo and space-Riesz fractional diffusion equation, Commun. Appl. Math. Comput., 2020, 2(1), 57-72. -
-
Figures(7) / Tables(5)
Export File
Citation
H. Dehestani, Y. Ordokhani. IMPROVEMENT OF THE SPECTRAL METHOD FOR SOLVING MULTI-TERM TIME-SPACE RIESZ-CAPUTO FRACTIONAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2600-2620. doi: 10.11948/20220146
Format
Content
DownLoad:
-
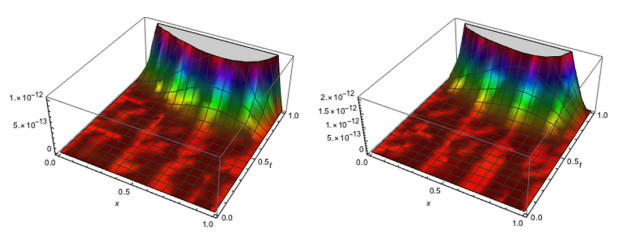
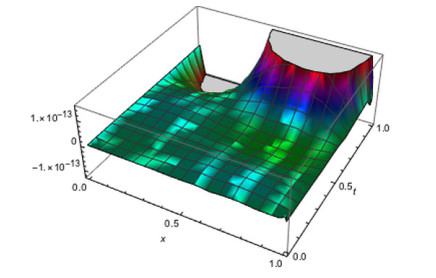
Figure 1.
The absolute error for
$ M_{1}=3,M_{2}=2 $ $ \alpha=0.8 $ $ \beta=1.25 $ -
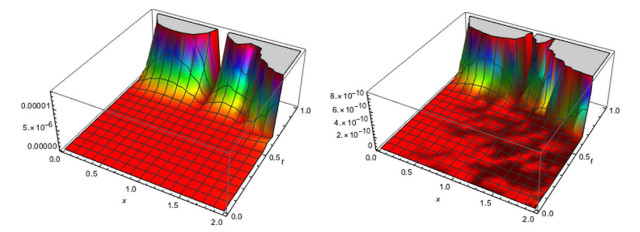
Figure 2.
The absolute error for
$ \beta=1.5 $ $ \beta=1.9 $ $ M_{1}=5,M_{2}=4 $ -
Figure 3.
The absolute error for
$ M_{2}=5 $ $ M_{2}=8 $ $ M_{1}=5, $ $ \beta=1.6 $ $ L=2 $ -
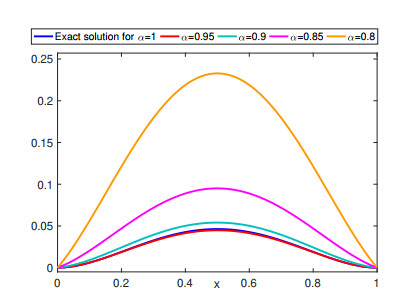
Figure 4.
Approximate solution for diverse values of
$ \alpha $ $ M_{2}=M_{1}=5, $ $ \beta=1.3 $ $ L=1 $ $ t=0.8 $ -
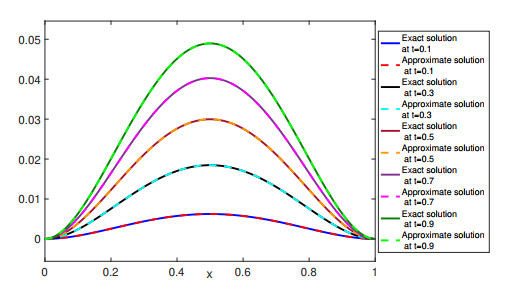
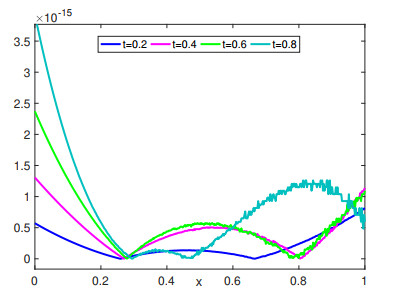
Figure 5.
Approximate solution at diverse times
$ t=0.1,0.3,0.5,0.7,0.9 $ $ M_{1}=M_{2}=5 $ $ \beta=1.9 $ -
Figure 6.
Error for
$ \alpha=0.75,\nu=0.35,\gamma=0.45,\beta=1.5 $ $ M_{1}=3,M_{2}=2 $ -
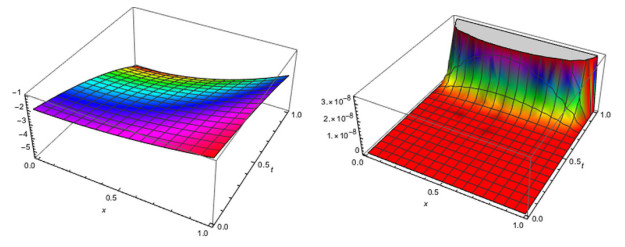
Figure 7.
The approximate solution (left) and the absolute error (right) for
$ \beta=1.3 $ $ M_{1}=3,M_{2}=8 $