| Citation: | Shitao Liu, Mingkang Ni. NONLINEAR SINGULAR SINGULARLY PERTURBED BOUNDARY VALUE PROBLEMS WITH DISCONTINUOUS RIGHT-HAND SIDE[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 845-859. doi: 10.11948/20220169 |
NONLINEAR SINGULAR SINGULARLY PERTURBED BOUNDARY VALUE PROBLEMS WITH DISCONTINUOUS RIGHT-HAND SIDE
-
Abstract
In this paper, an asymptotic method for nonlinear singular singularly perturbed boundary value problems with discontinuous right-hand side is investigated. We not only show existence of a solution with a step-like contrast structure, but also construct an asymptotic expansion of the solution. In addition, remainder estimation of the approximate solution is also given. Finally, an example is used to verify the correctness of the above theory.
-

-
References
[1] H. Chen and M. Ni, A singular approach to a class of impulsive differential equations, Journal of Applied Analysis and Computation, 2016, 6(4), 1195–1204. [2] H. Ding, M. Ni, W. Lin and Y. Cao, Singularly perturbed semi-linear boundary value problem with discontinuous function, Acta Mathematica Scientia, 2012, 32(2), 793–799. doi: 10.1016/S0252-9602(12)60059-9 [3] N. Fenichel, Geometric singular perturbation theory for ordinary differential equations, Journal of Differential Equations, 1979, 31(1), 53–98. doi: 10.1016/0022-0396(79)90152-9 [4] A. Kelley, The stable, center-stable, center, center-unstable, and unstable manifolds. Published as Appendix C of R. Abraham and J. Robbin: Transversal mappings and flows, New York, Benjamin, 1967. [5] N. N. Nefedov and M. Ni, Internal layers in the one dimensional reaction-diffusion equation with a discontinuous reactive term, Computational Mathematics and Mathematical Physics, 2015, 55(12), 2001–2007. doi: 10.1134/S096554251512012X [6] M. Ni, X. Qi and N. T. Levashova, Internal layer for a singularly perturbed equation with discontinuous right-hand side, Differential Equations, 2020, 56(10), 1276–1284. doi: 10.1134/S00122661200100031 [7] R. E. O'Malley and J. E. Flaherty, Analytical and numerical methods for nonlinear singular singularly-perturbed initial value problems, SIAM Journal on Applied Mathematics, 1980, 38(2), 225–248. doi: 10.1137/0138020 [8] C. Schmeiser and R. Weiss, Asymptotic analysis of singular singularly perturbed boundary value problems, SIAM Journal on Mathematical Analysis, 1986, 17(3), 560–579. doi: 10.1137/0517042 [9] A. B. Vasil'eva and V. F. Butuzov, Asymptotic Expansions of the Solutions of Singularly Perturbed Equations, Nauka, Moscow, 1973. [10] A. B. Vasil'eva and V. F. Butuzov, Singularly Perturbed Equations in the Critical Case, Moscow State University, Mathematics Research Center, Madison, 1980. [11] N. Wang, A class of singularly perturbed delayed boundary value problem in the critical case, Advances in Difference Equations, 2015, 212, 1–21. [12] X. Wu and M. Ni, Existence and stability of periodic contrast structure in reaction-advection-diffusion equation with discontinuous reactive and convective terms, Communications in Nonlinear Science and Numerical Simulation, 2020, 91, 1–16. [13] Q. Yang and M. Ni, Asymptotics of a class of singularly perturbed weak nonlinear boundary value problem with a multiple root of the degenerate equation, Journal of Nonlinear Modeling and Analysis, 2022, 4(3), 1–11. [14] Q. Yang and M. Ni, Asymptotics of the solution to a stationary piecewise-smooth reaction-diffusion equation with a multiple root of the degenerate equation, Science China Mathematics, 2022, 65(2), 291–308. doi: 10.1007/s11425-020-1856-4 -
-
-
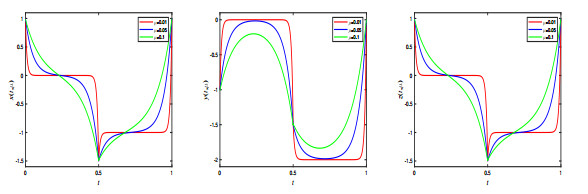
Figure 1.
The asymptotic solutions
$ x(t, \mu) $ $ y(t, \mu) $ $ z(t, \mu) $ $ \mu $




 DownLoad:
DownLoad: