| Citation: |
Hongyu Chen, Chunrui Zhang. BIFURCATIONS AND HYDRA EFFECTS IN A REACTION-DIFFUSION PREDATOR-PREY MODEL WITH HOLLING Ⅱ FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 424-444. doi: 10.11948/20220221
|
BIFURCATIONS AND HYDRA EFFECTS IN A REACTION-DIFFUSION PREDATOR-PREY MODEL WITH HOLLING Ⅱ FUNCTIONAL RESPONSE
-
Abstract
In this paper, through bifurcation analysis and numerical simulations, we consider a reaction-diffusion predator-prey model with Holling Ⅱ functional response to analyze the existence of hydra effect and the relationship between mortality independent of predator density and different steady-state solutions of the system. The hydra effect, which is a paradoxical result in both theoretical and applied ecology, refers to the phenomenon in which an increase in population mortality enhances its own population size. We investigate the existence of the hydra effect when the positive equilibrium point is locally asymptotically stable and Turing unstable. Meanwhile, numerical simulations verify the existence of the hydra effect when the one-dimensional reaction-diffusion system has a spatially inhomogeneous steady-state solution. In addition, we introduce the existence of the Turing bifurcation, the Hopf bifurcation, and the Turing-Hopf bifurcation with the parameters $ d_{2} $ and $ m_{C} $, respectively, as well as the normal form for the Turing-Hopf bifurcation. Based on the obtained normal form, we analyze the complex spatio-temporal dynamics near the Turing-Hopf bifurcation point. Finally, the numerical simulations are carried out to corroborate the obtained theoretical results.
-
Keywords:
- Predator-prey system /
- hydra effect /
- Turing instability /
- Turing-Hopf bifurcation /
- normal form
-
-
References
[1] P. A. Abrams and C. Quince, The impact of mortality on predator population size and stability in systems with stage-structured prey, Theor. Popul. Biol., 2005, 68(4), 253-266. doi: 10.1016/j.tpb.2005.05.004 [2] P. A. Abrams, What are hydra effects? A response to Schroder et al. , Trends Ecol. Evol., 2015, 30(4), 179-180. doi: 10.1016/j.tree.2015.01.013 [3] P. D. Adhikary, S. Mukherjee and B. Ghosh, Bifurcations and hydra effects in Bazykin's predator-prey model, Theor. Popul. Biol., 2021, 140, 44-53. doi: 10.1016/j.tpb.2021.05.002 [4] L. D. Anjos, M. I. D. Costa and R. C. Almeida, Characterizing the existence of hydra effect in spatial predator-prey models and the influence of functional response types and species dispersal, Ecol. Model., 2020, 428, 109109. doi: 10.1016/j.ecolmodel.2020.109109 [5] N. Bajeux and B. Ghosh, Stability switching and hydra effect in a predator-prey metapopulation model, Biosystems, 2021, 198. [6] M. H. Cortez and P. A. Abrams, Hydra effects in stable communities and their implications for system dynamics, Ecology, 2016, 97(5), 1135-1145. doi: 10.1890/15-0648.1 [7] X. Cao and W. Jiang, Turing-Hopf bifurcation and spatiotemporal patterns in a diffusive predator-prey system with Crowley-Martin functional response, Nonlinear Anal. Real World Appl., 2018, 43, 428-450. doi: 10.1016/j.nonrwa.2018.03.010 [8] M. H. Cortez and M. Yamamichi, How (co)evolution alters predator responses to increased mortality: extinction thresholds and hydra effects, Ecology, 2019, 100(10). [9] M. I. D. Costa and L. D. Anjos, Multiple hydra effect in a predator-prey model with Allee effect and mutual interference in the predator, Ecol. Model., 2018, 373, 22-24. doi: 10.1016/j.ecolmodel.2018.02.005 [10] H. Chen and C. Zhang, Analysis of the dynamics of a predator-prey model with Holling functional response, JNMA, 2022, 4(2), 310-324. [11] M. H. Cortez, Hydra effects in discrete-time models of stable communities, J. Theor. Biol., 2017, 411, 59-67. [12] D. L. DeAngelis and S. Yurek, Spatially explicit modeling in ecology: a review, Ecosystems, 2017, 20(2), 284-300. doi: 10.1007/s10021-016-0066-z [13] K. Garain and P. S. Mandal, Bubbling and hydra effect in a population system with Allee effect, Ecol. Complex, 2021, 47, 100939. doi: 10.1016/j.ecocom.2021.100939 [14] B. Ghosh, O. L. Zhdanova, B. Barman and E. Y. Frisman, Dynamics of stage-structure predator-prey systems under density-dependent effect and mortality, Ecol. Complex, 2020, 41, 100812. doi: 10.1016/j.ecocom.2020.100812 [15] W. Jiang, Q. An and J. Shi, Formulation of the normal form of Turing-Hopf bifurcation in partial functional differential equations, J. Differ. Equ., 2020, 268(10), 6067-6102. doi: 10.1016/j.jde.2019.11.039 [16] Z. Liu and R. Yang, Hopf bifurcation analysis of a Host-generalist parasitoid model with diffusion term and time delay, JNMA, 2021, 3(3), 447-463. [17] K. M. McIntire and S. A. Juliano, How can mortality increase population size? A test of two mechanistic hypotheses, Ecology, 2018, 99(7), 1660-1670. doi: 10.1002/ecy.2375 [18] D. Pal, B. Ghosh and T. K. Kar, Hydra effects in stable food chain models, Biosystems, 2019, 185, 104018. doi: 10.1016/j.biosystems.2019.104018 [19] C. Qin, J. Du and Y. Hui, Dynamical behavior of a stochastic predator-prey model with Holling-type Ⅲ functional response and infectious predator, AIMS Math., 2022, 7(5), 7403-7418. doi: 10.3934/math.2022413 [20] Y. Song, J. Shi and H. Wang, Spatiotemporal dynamics of a diffusive consumer-resource model with explicit spatial memory, Stud. Appl. Math., 2021, 148(1), 373-395. [21] Q. Song, R. Yang, C. Zhang and L. Wang, Bifurcation analysis of a diffusive predator-prey model with Beddington-Deangelis functional response, J. Appl. Anal. Comput., 2021, 11(2), 920-936. [22] Y. Song, T. Zhang and Y. Peng, Turing-Hopf bifurcation in the reaction-diffusion equations and its applications, Commun. Nonlinear Sci. Numer. Simul., 2015, 33, 229-258. [23] A. Schroder, L. Persson and A. M. D. Roos, Culling experiments demonstrate size-class specific biomass increases with mortality, Proc. Natl. Acad. Sci. USA, 2009, 106(8), 2671-2676. doi: 10.1073/pnas.0808279106 [24] A. Schroder, A. van Leeuwen and T. C. Cameron, When less is more: positive population-level effects of mortality, Trends Ecol. Evol., 2014, 29(11), 614-624. doi: 10.1016/j.tree.2014.08.006 [25] M. Sieber and F. M. Hilker, The hydra effect in predator-prey models, J. Math. Biol., 2012, 64(1-2), 341-360. doi: 10.1007/s00285-011-0416-6 [26] X. Tian and S. Guo, Spatio-temporal patterns of predator-prey model with Allee effect and constant stocking rate for predator, Int. J. Bifurcation Chaos, 2021, 31(16), 2150249. doi: 10.1142/S0218127421502497 [27] R. Wang and W. Zhao, Extinction and stationary distribution of a stochastic predator-prey model with Holling Ⅱ functional response and stage structure of prey, J. Appl. Anal. Comput., 2022, 12(1), 50-68. [28] L. Wang, C. Dai and M. Zhao, Hopf bifurcation in an age-structured prey-predator model with Holling Ⅲ response function, Math. Biosci. Eng., 2021, 18(4), 3144-3159. doi: 10.3934/mbe.2021156 [29] V. Weide, M. C. Varriale and F. M. Hilker, Hydra effect and paradox of enrichment in discrete-time predator-prey models, Math. Biosci., 2019, 317. [30] Y. Zhou, X. Yan and C. Zhang, Turing patterns induced by self-diffusion in a predator-prey model with schooling behavior in predator and prey, Nonlinear Dyn., 2021, 105(4), 3731-3747. doi: 10.1007/s11071-021-06743-2 -
-
Figures(12)
Export File
Citation
Hongyu Chen, Chunrui Zhang. BIFURCATIONS AND HYDRA EFFECTS IN A REACTION-DIFFUSION PREDATOR-PREY MODEL WITH HOLLING Ⅱ FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 424-444. doi: 10.11948/20220221
Format
Content
DownLoad:
-
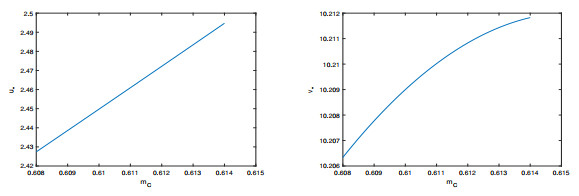
Figure 1.
The existence of the hydra effect is depicted when the system is in a stable state. The parameters value are
$ r=5.01, K=6.01, a_{CR}=1.01, Th_{CR}=1, ef_{RC}=1, q_{C}=0.01 $ -
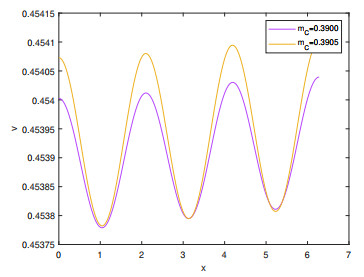
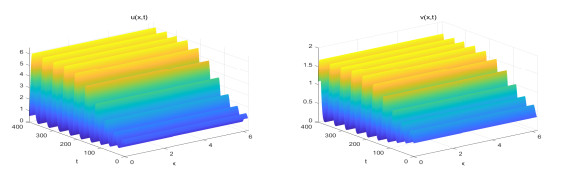
Figure 2.
Spatial distribution of predator population size when the other parameters are fixed at values:
$ d_{1}=0.01, d_{2}=2.51, r=0.25, K=14.95, a_{CR}=1.01, Th_{CR}=1, \alpha=2.61, \beta=0.61, l=1, x\in(0,2\pi) $ $ m_{C} $ -
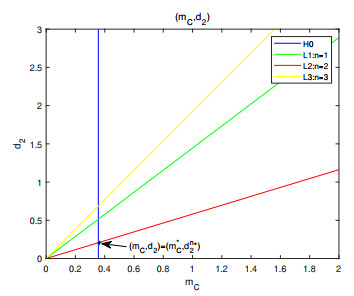
Figure 3.
Turing-Hopf bifurcation point
$ (m_{C}^{*},d_{2}^{n_{*}}) $ $ m_{C}-d_{2} $ -
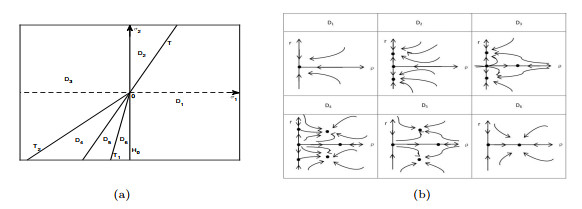
Figure 4.
The bifurcation set
$ (a) $ $ (b) $ -
Figure 5.
When
$ (\sigma_{1},\sigma_{2})=(1,0) $ $ D_{1} $ $ E_{*}(u_{*},v_{*})=(0.9483,0.4539) $ $ u(x,0)=0.94, v(x,0)=0.45 $ -
Figure 6.
When
$ (\sigma_{1},\sigma_{2})=(1,1) $ $ D_{2} $ $ E_{*}(u_{*},v_{*})=(0.9483,0.4539) $ $ cos(2x) $ -
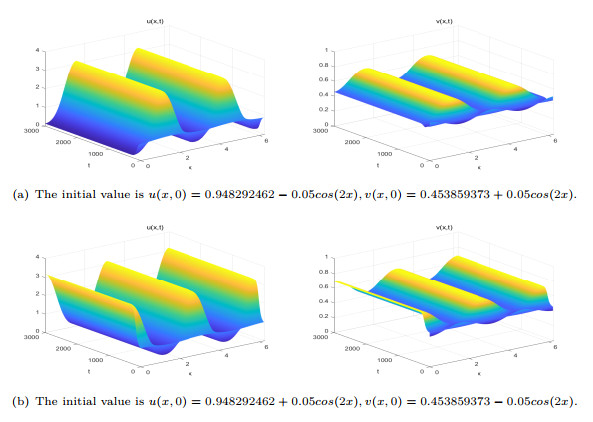
Figure 7.
When
$ (\sigma_{1},\sigma_{2})=(-0.1,0) $ $ D_{3} $ $ E_{*}(u_{*},v_{*})=(0.9483,0.4539) $ $ cos(2x) $ -
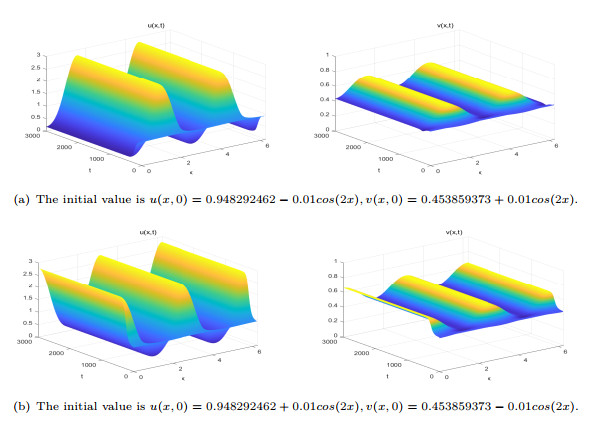
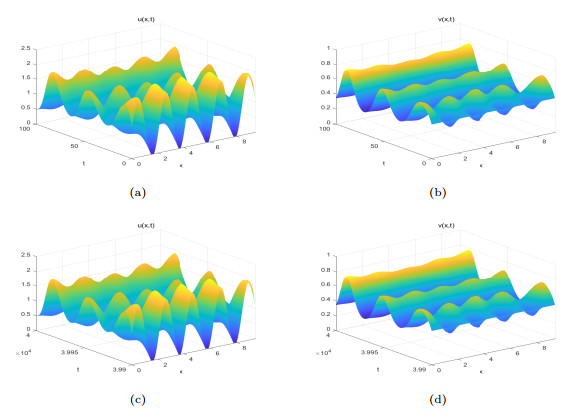
Figure 8.
When
$ (\sigma_{1},\sigma_{2})=(-0.1,-0.04) $ $ D_{4} $ $ E_{*}(u_{*},v_{*})=(0.9483,0.4539) $ $ u(x,0)=0.948292462+sin(2x), v(x,0)=0.453859373 $ $ u $ $ v $ $ u $ $ v $ -
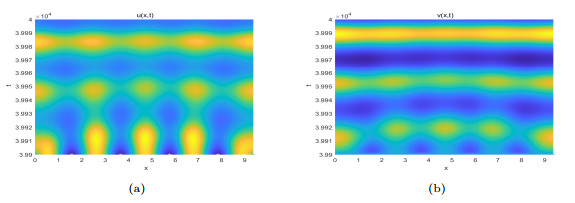
Figure 9.
$ (a) $ $ (b) $ $ x-t $ -
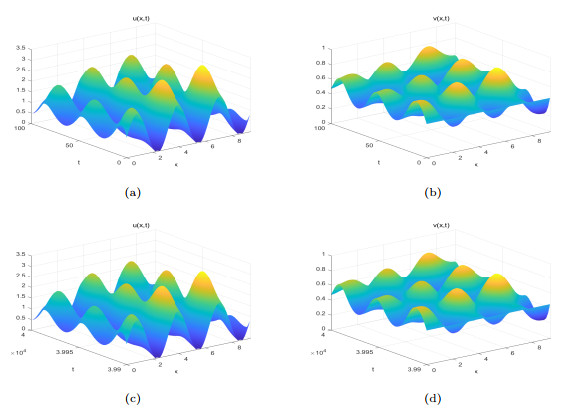
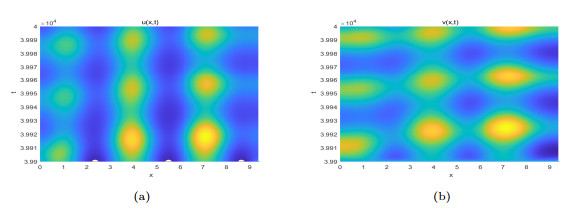
Figure 10.
When
$ (\sigma_{1},\sigma_{2})=(-0.1,-0.1) $ $ D_{5} $ $ E_{*}(u_{*},v_{*})=(0.9483,0.4539) $ $ u(x,0)=0.948292462+sin(3x), v(x,0)=0.453859373 $ $ u $ $ v $ $ u $ $ v $ -
Figure 11.
$ (a) $ $ (b) $ $ x-t $ -
Figure 12.
When
$ (\sigma_{1},\sigma_{2})=(-0.1,-0.2) $ $ D_{6} $ $ E_{*}(u_{*},v_{*})=(0.9483,0.4539) $ $ u(x,0)=0.948292462+0.1, v(x,0)=0.453859373-0.1 $