| Citation: |
Fu Feng, Jianping Shi, Hui Fang. HOPF BIFURCATION OF A FRACTIONAL-ORDER PREY-PREDATOR-SCAVENGER SYSTEM WITH HUNTING DELAY AND COMPETITION DELAY[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1234-1258. doi: 10.11948/20220253
|
HOPF BIFURCATION OF A FRACTIONAL-ORDER PREY-PREDATOR-SCAVENGER SYSTEM WITH HUNTING DELAY AND COMPETITION DELAY
-
Abstract
This paper deals with Hopf bifurcation of a fractional-order prey-predator-scavenger system (FPSS in short) with hunting delay and two-predator competition delay. We introduce the notion of Hopf bifurcation of fractional-order system with double delays. The characteristic equation of the linearized system of FPSS is obtained by using the method of linearization and Laplace transform. Choosing the hunting delay and the competition delay as bifurcation parameters, respectively, we obtain the stability switch conditions and the critical delay values of emergence of Hopf bifurcation by analyzing the characteristic equation of the linearized system around a coexistence equilibrium. Especially, the delay bifurcation curve of emergence of Hopf bifurcation for FPSS with nonzero double delays is determined. Numerical simulations are performed to further illustrate our theoretical results.
-
-
References
[1] W. Abid, R. Yafia, M.A. Aziz-Alaoui, H. Bouhafa, A. Abichou, Diffusion driven instability and Hopf bifurcation in spatial predator-prey model on a circular domain, Appl. Math. Comput., 2015, 1(2015), 292–313. [2] H. N. Agiza, et al. Chaotic dynamics of a discrete prey-predator model with Holling type Ⅱ, Nonlinear Anal-real, 2009, 10(1), 116–129. doi: 10.1016/j.nonrwa.2007.08.029 [3] E. Ahmed, A. M. A. El-Sayed, et al., Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models, J. Math. Anal. Appl., 2007, 325(1), 542–553. doi: 10.1016/j.jmaa.2006.01.087 [4] J. Alidoust, Stability and bifurcation analysis for a fractional prey-predator scavenger model, Appl. Math. Model., 2020, 81(5), 342–355. [5] E. Ahmed, A. El-ssyed, H. EL-saka, On some Routh-Hurwitz conditions for fractional order differential equations and their applications in LORENZ, RSSLER, CHUA and CHEN systems, Phys. Lett. A, 2006, 358(1), 1–4. doi: 10.1016/j.physleta.2006.04.087 [6] S. Boonrangsiman, K. Bunwong, E. J. Moore, A bifurcation path to chaos in a time-delay fisheries predator-prey model with prey consumption by immature and mature predators, Math. Comput. Simulat., 2016, 124(2016), 16–29. [7] J. Banasiak, M. S. S. Tchamga, Delayed stability switches in singularly perturbed predator-prey models, Nonlinear Anal., 2017, 35(2017), 312–335. [8] Y. Du, J. Shi, Some recent results on diffusive predator-prey models in spatially heterogeneous environment, Nonlinear Dynam. Evol. Equa., 2006. DOI: 10.1090/fic/048/05. [9] K. Das, T. K. Kar, Dynamical Analysis of an Exploited Prey-Predator System in Fuzzy Environment, Int. J. Ecol. Econ. Stat., 2020, 41(2). [10] U. Das, T. K. Kar, S. Jana, Dynamical behaviour of a delayed stage-structured predator-prey model with nonmonotonic functional response, Int. J. Dynam. Control, 2015, 3, 225–238. doi: 10.1007/s40435-014-0110-9 [11] W. Deng, C. Li, J. Lu, Stability analysis of linear fractional differential system with multiple time delays, Nonlinear Dynam., 2006, 48(4), 409–416. [12] A. A. Elsadany, A. E. Matouk, Dynamical behaviors of fractional-order Lotka-Volterra predator-prey model and its discretization, J. Appl. Math. Comput., 2015, 49(2015), 269–283. [13] S. F. Gilbert, Aphid suitability and its relationship to oviposition preference in predatory hoverflies, J. Anim. Ecol., 2000, 69(5), 771–784. doi: 10.1046/j.1365-2656.2000.00433.x [14] S. Gakkhar, R. K. Naji, Chaos in seasonally perturbed ratio-dependent prey-predator system, Chaos. Solitons. Fract, 2003, 15(1), 107–118. doi: 10.1016/S0960-0779(02)00114-5 [15] Y. Huang, L. Zhang, S. Fang, Coexistence of a strongly coupled prey-predator model for Holling type Ⅲ, Chinese Quarterly Journal of Mathematics, 2009, 24(3), 389–393. [16] C. Huang, J. Cao, X. Min, et al., Controlling bifurcation in a delayed fractional predator-prey system with incommensurate orders, Appl. Math. Comput., 2017, 293(C), 293–310. [17] D. Kai, The Analysis of Fractional Differential Equations. Springer Berlin Heidelberg, 2010. [18] D. Kai, N. J. Ford, A. D. Freed, A Predictor-Corrector Approach for the Numerical Solution of Fractional Differential Equations, Nonlinear Dynam., 2002, 29(1–4), 3–22. [19] H, Li, C. Huang, T. Li, Dynamic complexity of a fractional-order predator-prey system with double delays, Physica A, 2019, 526. [20] X. Liu, H. Fang, Periodic pulse control of Hopf bifurcation in a fractional-order delay predator-prey model incorporating a prey refuge, Adv. Differ. Equ-NY, 2019, 2019(1). DOI: 10.1186/s13662-019-2413-9. [21] P. S. Mandal, M. Banerjee, Stochastic persistence and stationary distribution in a Holling-Tanner type prey-predator model, Physica A, 2012, 391(4), 1216–1233. doi: 10.1016/j.physa.2011.10.019 [22] A. Matsumoto, F. Szidarovszky, Stability switching curves in a Lotka-Volterra competition system with two delays, Math. Comput. Simulat., 2020, 178(C), 422–438. [23] X. Min, G. Jiang, J. Cao, et al., Local Bifurcation Analysis of a Delayed Fractional-Order Dynamic Model of Dual Congestion Control Algorithms, IEEE/CAA J. Auto. Sini., 2017, 99(2017), 361–369. [24] I. Petras, Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation, Higher Education Press, Beijing and Springer-Verlag, Berlin Heidelberg, 2011. [25] P. Panja, Stability and dynamics of a fractional-order three-species predator-prey model, Theor. Biosci., 2019, 138, 251–259. doi: 10.1007/s12064-019-00291-5 [26] I. Podlubny, Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Math. Sci. Eng., 2013, 2013(3), 553–563. [27] M. Rivero, J. J. Trujillo, L. Vzquez, M. P. Velasco, Fractional dynamics of population, Appl. Math. Comput., 2011, 218, 1089–1095. doi: 10.1016/j.amc.2011.03.017 [28] F. A. Rihan, S. Lakshmanan, A. H. Hashish, et al, Fractional-order delayed predator-prey systems with Holling type-Ⅱ functional response, Nonlinear Dynam., 2015, 80(2), 777–789. [29] H. A. Satar, R. K. Naji, Stability and Bifurcation of a Prey-Predator-Scavenger Model in the Existence of Toxicant and Harvesting, Int. J. Math. Math. Sci., 2019, 1–17. [30] P. Song, H. Y. Zhao, X. B. Zhang, Dynamic analysis of a fractional order delayed predator-prey system with harvesting, Theor. Biosci., 2016, 135(2016), 1–14. [31] H. A. Satar, R. K. Naji, Stability and Bifurcation of a Prey-Predator-Scavenger Model in the Existence of Toxicant and Harvesting, Int. J. Math. Math. Sci., 2019. DOI: 10.1155/2019/1573516. [32] X. Wang, W. Wang, Y. Lin, et al., The dynamical complexity of an impulsive Watt-type prey-predator system, Chaos. Solitons. Fract., 2009, 40(2), 731–744. doi: 10.1016/j.chaos.2007.08.019 [33] B. J. West, Colloquium: Fractional calculus view of complexity: A tutorial, Rev. mod. Phys., 2014, 86(4), 1169–1186. doi: 10.1103/RevModPhys.86.1169 -
-
Figures(12) / Tables(2)
Export File
Citation
Fu Feng, Jianping Shi, Hui Fang. HOPF BIFURCATION OF A FRACTIONAL-ORDER PREY-PREDATOR-SCAVENGER SYSTEM WITH HUNTING DELAY AND COMPETITION DELAY[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1234-1258. doi: 10.11948/20220253
Format
Content
DownLoad:
-
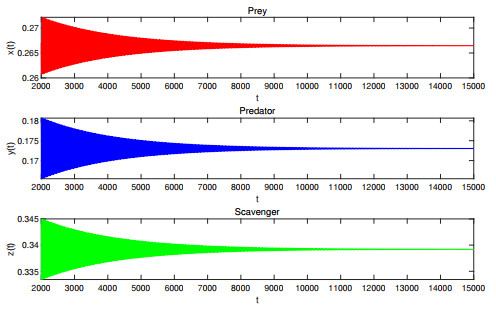
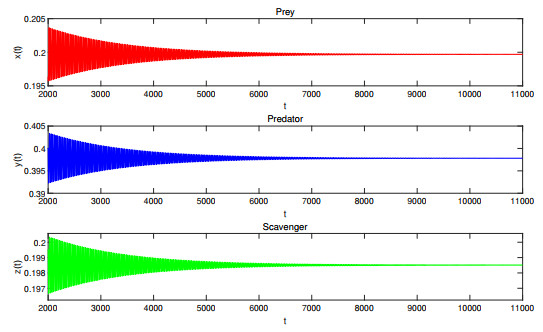
Figure 1. Waveform plots of Case Ⅱ with
$ \tau_1=\tau_2=12.5<\tau_0=12.7408 $ . The coexistence equilibrium point$ E_7 $ of system (4.1) is asymptotically stable. -
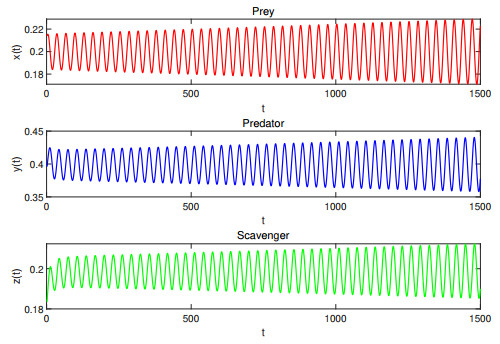
Figure 2. Waveform plots of Case Ⅱ with
$ \tau_1=\tau_2=12.8>\tau_0=12.7408 $ . System (4.1) undergoes periodic oscillation. -
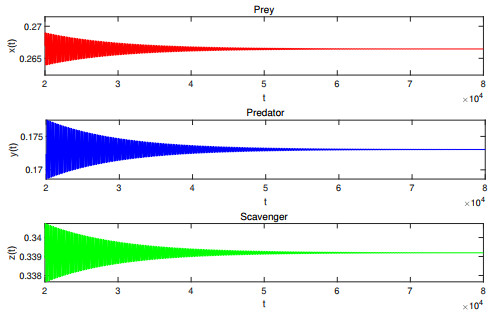
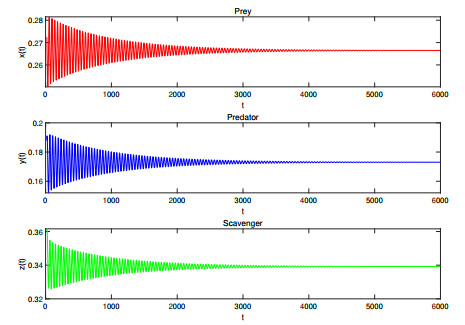
Figure 3. Waveform plots of Case Ⅴ with
$ \tau_1=0, \tau_2=93.5<\bar{\tau}_2=94.22664 $ . The coexistence equilibrium point$ E_7 $ of (4.1) is asymptotically stable. -
Figure 4. Waveform plots of Case Ⅴ with
$ \tau_1=0, \tau_2=94.6>\bar{\tau}_2=94.22664 $ . System (4.1) undergoes periodic oscillation. -
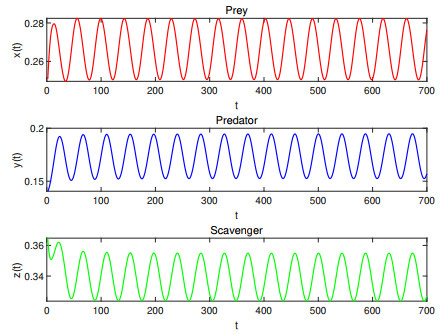
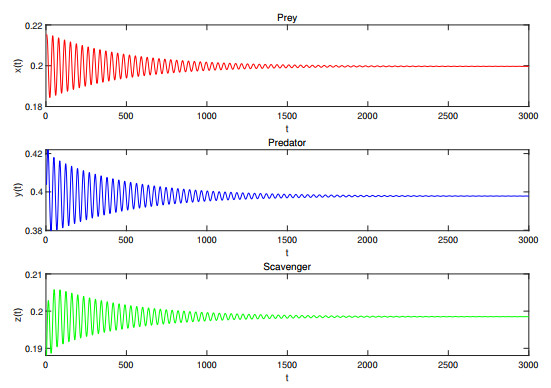
Figure 5. Waveform plots of Case Ⅵ with
$ \tau_1=13.4<13.84928, \tau_2=12 $ . The coexistence equilibrium point$ E_7 $ of system (4.1) is asymptotically stable. -
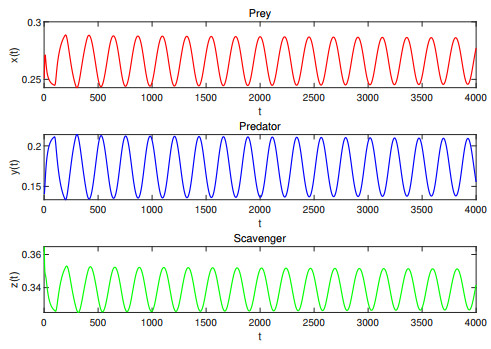
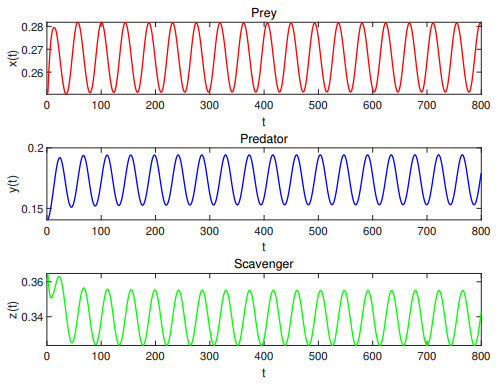
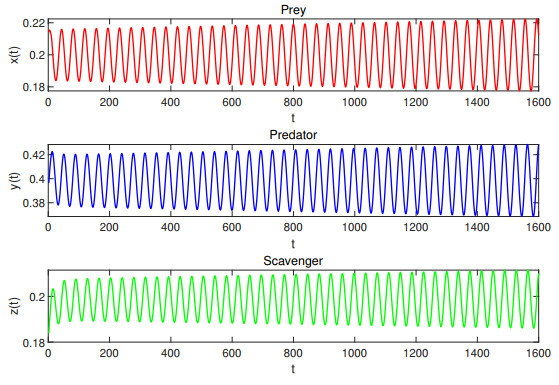
Figure 6. Waveform plots of Case Ⅵ with
$ \tau_1=14>13.84928, \tau_2=12 $ . System (4.1) undergoes periodic oscillation. -
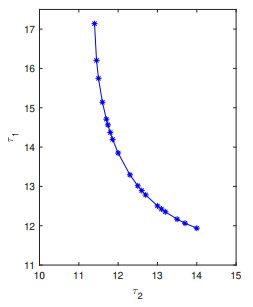
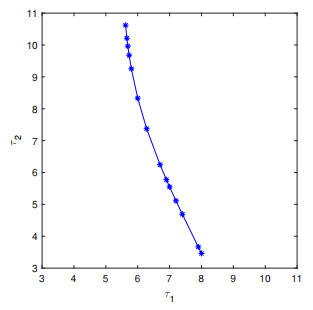
Figure 7. The delay bifurcation curve
$ S_1 $ on the$ (\tau_2, \tau_1) $ -plane in Case Ⅵ. -
Figure 8. Waveform plots of Case Ⅲ with
$ \tau_1=9.1<\bar{\tau}_1=9.52225, \tau_2=0 $ . The coexistence equilibrium point$ E_7 $ of system (4.2) is asymptotically stable. -
Figure 9. Waveform plots of Case Ⅲ with
$ \tau_1=9.7>\bar{\tau}_1=9.52225, \tau_2=0 $ . System (4.2) undergoes periodic oscillation. -
Figure 10. Waveform plots of Case Ⅳ with
$ \tau_1=6, \tau_2=8<\bar{\tau}_{2}=8.33174 $ . The coexistence equilibrium point$ E_7 $ of system (4.2) is asymptotically stable. -
Figure 11. Waveform plots of Case Ⅵ with
$ \tau_1=6, \tau_2=8.5>\bar{\tau}_{2}=8.33174 $ . System (4.2) undergoes periodic oscillation. -
Figure 12. The delay bifurcation curve
$ S_2 $ on the$ (\tau_1, \tau_2) $ -plane in Case Ⅳ.