| Citation: |
Ahmed Z. Amin, António M. Lopes, Ishak Hashim. A SPACE-TIME SPECTRAL COLLOCATION METHOD FOR SOLVING THE VARIABLE-ORDER FRACTIONAL FOKKER-PLANCK EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 969-985. doi: 10.11948/20220254
|
A SPACE-TIME SPECTRAL COLLOCATION METHOD FOR SOLVING THE VARIABLE-ORDER FRACTIONAL FOKKER-PLANCK EQUATION
-
Abstract
A numerical approach for solving the variable-order fractional Fokker-Planck equation (VO-FFPE) is proposed. The computational scheme is based on the shifted Legendre Gauss-Lobatto and the shifted Chebyshev Gauss-Radau collocation methods. The VO-FFPE is written as a truncated series of shifted Legendre and shifted Chebyshev polynomials for space and time variables, respectively. The residuals of the VO-FFPE at the shifted Legendre Gauss-Lobatto and shifted Chebyshev Gauss-Radau quadrature points are estimated. The original problem is converted into a system of algebraic equations that can be solved easily. Several examples are presented to demonstrate the efficacy of the technique.
-
-
References
[1] M. Abdelkawy, A. Amin and A. M. Lopes, Fractional-order shifted Legendre collocation method for solving non-linear variable-order fractional Fredholm integro-differential equations, Computational and Applied Mathematics, 2022, 41(1), 1–21. doi: 10.1007/s40314-021-01695-0 [2] H. Abo-Gabal, M. A. Zaky, A. S. Hendy and E. H. Doha, Computational aspects of fractional romanovski–bessel functions, Computational and Applied Mathematics, 2021, 40(4), 1–16. [3] I. G. Ameen, M. A. Zaky and E. H. Doha, Singularity preserving spectral collocation method for nonlinear systems of fractional differential equations with the right-sided Caputo fractional derivative, Journal of Computational and Applied Mathematics, 2021, 392, 113468. doi: 10.1016/j.cam.2021.113468 [4] A. H. Bhrawy and M. A. Zaky, Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation, Nonlinear Dynamics, 2015, 80(1), 101–116. [5] A. H. Bhrawy and M. A. Zaky, Numerical algorithm for the variable-order Caputo fractional functional differential equation, Nonlinear Dynamics, 2016, 85(3), 1815–1823. doi: 10.1007/s11071-016-2797-y [6] A. H. Bhrawy and M. A. Zaky, Highly accurate numerical schemes for multi-dimensional space variable-order fractional Schrödinger equations, Computers & Mathematics with Applications, 2017, 73(6), 1100–1117. [7] A. H. Bhrawy and M. A. Zaky, An improved collocation method for multi-dimensional space–time variable-order fractional Schrödinger equations, Applied Numerical Mathematics, 2017, 111, 197–218. doi: 10.1016/j.apnum.2016.09.009 [8] C. Canuto, M. Y. Hussaini, A. Quarteroni and T. A. Zang, Spectral Methods: Fundamentals in Single Domains, Springer Science & Business Media, 2007. [9] L. Chen, W. Pan, R. Wu, et al., Design and implementation of grid multi-scroll fractional-order chaotic attractors, Chaos: An Interdisciplinary Journal of Nonlinear Science, 2016, 26(8), 084303. doi: 10.1063/1.4958717 [10] Y. Chen, L. Liu, B. Li and Y. Sun, Numerical solution for the variable order linear cable equation with Bernstein polynomials, Applied Mathematics and Computation, 2014, 238, 329–341. doi: 10.1016/j.amc.2014.03.066 [11] Y. Chen and J. Zhou, Error estimates of spectral Legendre–Galerkin methods for the fourth-order equation in one dimension, Applied Mathematics and Computation, 2015, 268, 1217–1226. doi: 10.1016/j.amc.2015.06.082 [12] G. L. Delzanno, Multi-dimensional, fully-implicit, spectral method for the Vlasov–Maxwell equations with exact conservation laws in discrete form, Journal of Computational Physics, 2015, 301, 338–356. doi: 10.1016/j.jcp.2015.07.028 [13] K. Diethelm, V. Kiryakova, Y. Luchko, et al., Trends, directions for further research, and some open problems of fractional calculus, Nonlinear Dynamics, 2022, 1–26. [14] E. Doha, M. Abdelkawy, A. Amin and D. Baleanu, Approximate solutions for solving nonlinear variable-order fractional Riccati differential equations, Nonlinear Analysis: Modelling and Control, 2019, 24(2). [15] E. Doha, M. Abdelkawy, A. Amin and A. M. Lopes, A space–time spectral approximation for solving nonlinear variable-order fractional sine and Klein–Gordon differential equations, Computational and Applied Mathematics, 2018, 37(5), 6212–6229. doi: 10.1007/s40314-018-0695-2 [16] E. H. Doha, M. A. Abdelkawy, A. Z. Amin and A. M. Lopes, Numerical solutions for variable-order fractional Gross–Pitaevskii equation with two spectral collocation approaches, International Journal of Nonlinear Sciences and Numerical Simulation, 2021. [17] E. H. Doha, M. A. Abdelkawy, A. Z. M. Amin and D. Baleanu, Spectral technique for solving variable-order fractional volterra integro-differential equations, Numerical Methods for Partial Differential Equations, 2018, 34(5), 1659–1677. doi: 10.1002/num.22233 [18] E. H. Doha, M. A. Abdelkawy, A. Z. M. Amin and A. M. Lopes, On spectral methods for solving variable-order fractional integro-differential equations, Computational and Applied Mathematics, 2018, 37(3), 3937–3950. doi: 10.1007/s40314-017-0551-9 [19] E. H. Doha, M. A. Abdelkawy, A. Z. M. Amin and A. M. Lopes, Shifted Jacobi–Gauss-collocation with convergence analysis for fractional integro-differential equations, Communications in Nonlinear Science and Numerical Simulation, 2019, 72, 342–359. doi: 10.1016/j.cnsns.2019.01.005 [20] N. A. Elkot, M. A. Zaky, E. H. Doha and I. G. Ameen, On the rate of convergence of the Legendre spectral collocation method for multi-dimensional nonlinear Volterra–Fredholm integral equations, Communications in Theoretical Physics, 2021, 73(2), 025002. doi: 10.1088/1572-9494/abcfb3 [21] H. Habenom and D. L. Suthar, Numerical solution for the time-fractional Fokker-Planck equation via shifted Chebyshev polynomials of the fourth kind, Advances in Difference Equations, 2020, 2020(1), 1–16. doi: 10.1186/s13662-019-2438-0 [22] R. M. Hafez, S. S. Ezz-Eldien, A. H. Bhrawy, et al., A Jacobi Gauss–Lobatto and Gauss–Radau collocation algorithm for solving fractional Fokker-Planck equations, Nonlinear Dynamics, 2015, 82(3), 1431–1440. doi: 10.1007/s11071-015-2250-7 [23] A. S. Hendy, M. A. Zaky, R. M. Hafez and R. H. De Staelen, The impact of memory effect on space fractional strong quantum couplers with tunable decay behavior and its numerical simulation, Scientific Reports, 2021, 11(1), 1–15. doi: 10.1038/s41598-020-79139-8 [24] C. Li and A. Chen, Numerical methods for fractional partial differential equations, International Journal of Computer Mathematics, 2018, 95(6-7), 1048–1099. doi: 10.1080/00207160.2017.1343941 [25] L. Pinto and E. Sousa, Numerical solution of a time-space fractional Fokker-Planck equation with variable force field and diffusion, Communications in Nonlinear Science and Numerical Simulation, 2017, 50, 211–228. doi: 10.1016/j.cnsns.2017.03.004 [26] H. Risken, Fokker-Planck equation, in The Fokker-Planck Equation, Springer, 1996, 63–95. [27] F. Song and C. Xu, Spectral direction splitting methods for two-dimensional space fractional diffusion equations, Journal of Computational Physics, 2015, 299, 196–214. doi: 10.1016/j.jcp.2015.07.011 [28] H. Sun, W. Chen, H. Wei and Y. Chen, A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems, The european physical journal special topics, 2011, 193(1), 185–192. doi: 10.1140/epjst/e2011-01390-6 [29] V. E. Tarasov, Fractional fokker–planck equation for fractal media, Chaos: An Interdisciplinary Journal of Nonlinear Science, 2005, 15(2), 023102. doi: 10.1063/1.1886325 [30] V. E. Tarasov, Fokker–planck equation for fractional systems, International Journal of Modern Physics B, 2007, 21(06), 955–967. doi: 10.1142/S0217979207036771 [31] V. E. Tarasov, Fokker-planck equation for fractal distributions of probability, in Fractional Dynamics, Springer, 2010, 123–133. [32] V. E. Tarasov, Fractional dynamics: applications of fractional calculus to dynamics of particles, fields and media, Springer Science & Business Media, 2011. [33] V. E. Tarasov, Large lattice fractional fokker–planck equation, Journal of Statistical Mechanics: Theory and Experiment, 2014, 2014(9), P09036. doi: 10.1088/1742-5468/2014/09/P09036 [34] V. E. Tarasov, Generalized memory: Fractional calculus approach, Fractal and Fractional, 2018, 2(4), 23. doi: 10.3390/fractalfract2040023 [35] V. E. Tarasov, Applications in Physics, Part B, De Gruyter, 2019. [36] V. E. Tarasov, Fractional econophysics: Market price dynamics with memory effects, Physica A: Statistical Mechanics and its Applications, 2020, 557, 124865. doi: 10.1016/j.physa.2020.124865 [37] V. E. Tarasov and V. V. Tarasova, Economic dynamics with memory: Fractional calculus approach, 8, Walter de Gruyter GmbH & Co KG, 2021. [38] V. E. Tarasov and G. M. Zaslavsky, Fokker–planck equation with fractional coordinate derivatives, Physica A: Statistical Mechanics and Its Applications, 2008, 387(26), 6505–6512. doi: 10.1016/j.physa.2008.08.033 [39] D. Tavares, R. Almeida and D. F. M. Torres, Caputo derivatives of fractional variable order: numerical approximations, Communications in Nonlinear Science and Numerical Simulation, 2016, 35, 69–87. doi: 10.1016/j.cnsns.2015.10.027 [40] J. P. Ugarte, C. Tobón, A. Mendes Lopes and J. A. Tenreiro Machado, Atrial rotor dynamics under complex fractional order diffusion, Frontiers in physiology, 2018, 9, 975. doi: 10.3389/fphys.2018.00975 [41] J. Xie, Z. Yao, H. Gui, et al., A two-dimensional Chebyshev waveletsapproach for solving the Fokker-Planck equations of time and space fractional derivatives type with variable coefficients, Applied Mathematics and Computation, 2018, 332, 197–208. doi: 10.1016/j.amc.2018.03.040 [42] M. A. Zaky, An accurate spectral collocation method for nonlinear systems of fractional differential equations and related integral equations with nonsmooth solutions, Applied Numerical Mathematics, 2020, 154, 205–222. doi: 10.1016/j.apnum.2020.04.002 [43] M. A. Zaky, A. S. Hendy and R. H. De Staelen, Alikhanov Legendre—Galerkin spectral method for the coupled nonlinear time-space fractional Ginzburg–Landau complex system, Mathematics, 2021, 9(2), 183. doi: 10.3390/math9020183 [44] M. A. Zaky, A. S. Hendy and D. Suragan, Logarithmic Jacobi collocation method for Caputo–Hadamard fractional differential equations, Applied Numerical Mathematics, 2022, 181(1), 326–346. [45] Z. Zhao and C. Li, A numerical approach to the generalized nonlinear fractional Fokker-Planck equation, Computers & Mathematics with Applications, 2012, 64(10), 3075–3089. -
-
Figures(10) / Tables(6)
Export File
Citation
Ahmed Z. Amin, António M. Lopes, Ishak Hashim. A SPACE-TIME SPECTRAL COLLOCATION METHOD FOR SOLVING THE VARIABLE-ORDER FRACTIONAL FOKKER-PLANCK EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 969-985. doi: 10.11948/20220254
Format
Content
DownLoad:
-
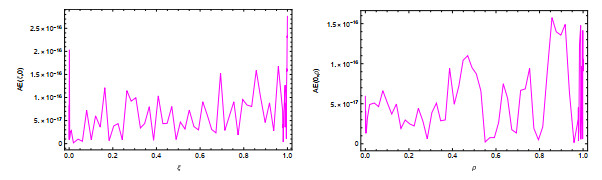
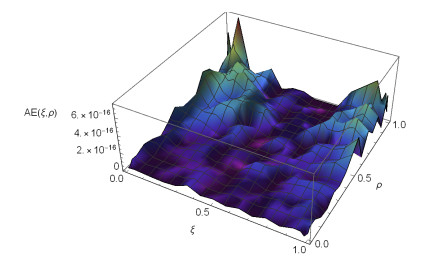
Figure 1.
$ \xi $ $ \rho $ $ AE $ $ \mu=\kappa=12 $ $ \sigma{(\xi, \rho)}=\frac{6+\sin(\xi)}{4} $ -
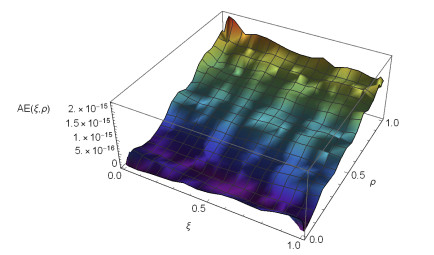
Figure 2.
$ \xi $ $ \rho $ $ AE $ $ \mu=\kappa=12 $ $ \sigma{(\xi, \rho)}=\frac{7+\xi\cos(\xi)}{3} $ -
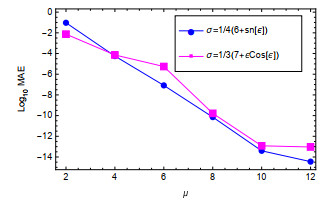
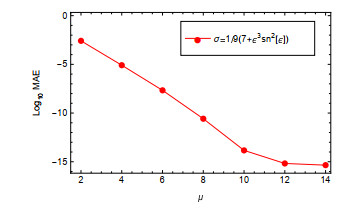
Figure 3.
The
$ \log_{10} MAE $ $ \mu $ $ \sigma{(\xi, \rho)}=\frac{6+\sin(\xi)}{4} $ $ \sigma{(\xi, \rho)}=\frac{7+\xi\cos(\xi)}{3} $ -
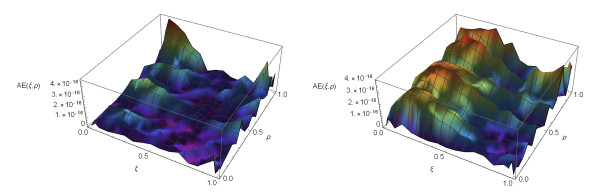
Figure 4.
The
$ AE $ $ \xi $ $ \rho $ $ \sigma(\xi, \rho)=\frac{6+\xi\sin^{2}(\xi)}{4} $ $ \sigma(\xi, \rho)=\frac{6+\xi\cos^{2}(\xi)}{4} $ $ \delta(\xi, \rho)=\xi\sin(\rho) $ $ \mu=\kappa=14 $ -
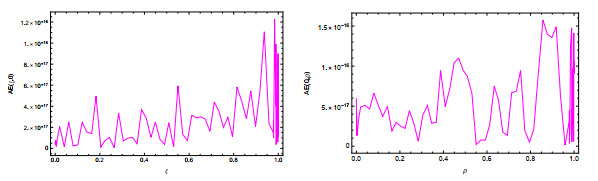
Figure 5.
$ \xi $ $ \rho $ $ AE $ $ \sigma(\xi, \rho)=\frac{3+\sin(\xi)}{7} $ $ \delta(\xi, \rho)=\xi^{3} \sin(\rho) $ $ \mu=\kappa=12 $ -
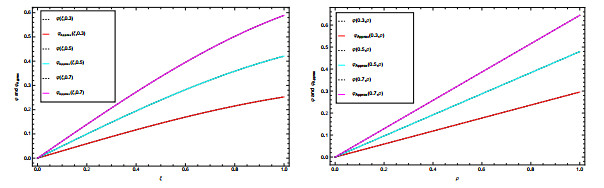
Figure 6.
The
$ \varphi_{ \rm{Approx}}(\xi, \rho) $ $ \varphi(\xi, \rho) $ $ \sigma(\xi, \rho)=\frac{3+\sin(\xi)}{7} $ $ \delta(\xi, \rho)=\xi^{3} \sin(\rho) $ $ \mu=\kappa=12 $ -
Figure 7.
The
$ AE $ $ \xi $ $ \rho $ $ \sigma(\xi, \rho)=\frac{3+\sin(\xi)}{7} $ $ \delta(\xi, \rho)=\xi^{3} \sin(\rho) $ $ \mu=\kappa=12 $ -
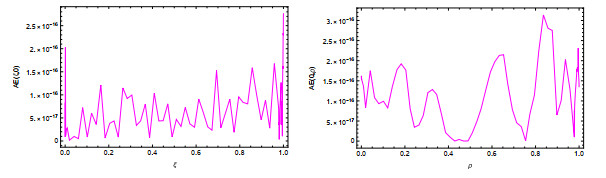
Figure 8.
The
$ \varphi_{ \rm{Approx}}(\xi, \rho) $ $ \varphi(\xi, \rho) $ $ \sigma(\xi, \rho)=\frac{7+\xi^{3}\sin^{2}(\xi)}{9} $ $ \delta(\xi, \rho)=\xi^{2}\sin(\rho) $ $ \mu=\kappa=14 $ -
Figure 9.
The
$ AE $ $ \sigma(\xi, \rho)=\frac{7+\xi^{3}\sin^{2}(\xi)}{9} $ $ \delta(\xi, \rho)=\xi^{2}\sin(\rho) $ $ \mu=\kappa=14 $ -
Figure 10.
The
$ \log_{10} MAE $ $ \mu $ $ \sigma(\xi, \rho)=\frac{7+\xi^{3}\sin^{2}(\xi)}{9} $ $ \delta(\xi, \rho)=\xi^{2}\sin(\rho) $