| Citation: | Qiuyan Zhang, Yuqian Zhou. BIFURCATIONS AND OBTAINED EXACT SOLUTIONS OF THE OPTICAL SOLITON MODEL IN METAMATERIALS DOMINATED BY ANTI-CUBIC NONLINEARITY[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1931-1971. doi: 10.11948/20220289 |
BIFURCATIONS AND OBTAINED EXACT SOLUTIONS OF THE OPTICAL SOLITON MODEL IN METAMATERIALS DOMINATED BY ANTI-CUBIC NONLINEARITY
-
Abstract
In this paper, we study the optical model in metamaterials with nonlinear influence of non-Kerr law and a few Hamiltonian perturbation terms. The nonlinearity of metamaterials is dominated by anti-cubic type. We apply the approach of dynamical system to find the travelling wave solutions of the optical model. Under different parameter conditions, bifurcations of phase portraits and exact periodic solutions, homoclinic and heteroclinic solutions, peakon, periodic peakons as well as compacton solutions for this planar dynamical system are given. By using the first integral, exact solutions of can be calculated under different parameter conditions. 83 exact explicit parametric representations are derived.
-
Keywords:
- Bifurcation /
- exact solution /
- optical soliton /
- anti-cubic nonlinearity
-

-
References
[1] S. S. Afzal, M. Younis and S. T. R. Rizvi, Optical dark and dark-singular solitons with anti-cubic nonlinearity, Optik, 2017, 147, 27–31. doi: 10.1016/j.ijleo.2017.08.067 [2] K. S. Al-Ghafri, Solitary wave solutions of two KdV-type equations, Open Phys. 2018, 16(1), 311–318. doi: 10.1515/phys-2018-0043 [3] K. S. Al-Ghafri1 and E. V. Krishnan, Optical solitons in metamaterials dominated by anti-cubic nonlinearity and Hamiltonian perturbations, Int. J. Appl. Comput. Math., 2020, 6(5), 144. doi: 10.1007/s40819-020-00896-1 [4] K. Al-Ghafri, E. Krishnan, A. Biswas, et al., Optical solitons having anti-cubic nonlinearity with a couple of exotic integration schemes, Optik, 2018, 172, 794–800. doi: 10.1016/j.ijleo.2018.07.101 [5] L. Alloatti, C. Kieninger, A. Froelich, et al., Second-order nonlinear optical metamaterials: ABC-type nanolaminates, Appl. Phys. Lett., 2015, 107(12), 121903. doi: 10.1063/1.4931492 [6] A. Arab, Exactly solvable supersymmetric quantum mechanics, J. Math. Anal. Appl., 1991, 158(1), 63–79. doi: 10.1016/0022-247X(91)90267-4 [7] A. Arab, Exact solutions of multi-component nonlinear Schrdinger and Klein-Gordon equations in two-dimensional space-time, J. Phys. A: Math. Gen., 2001, 34(20), 4281–4288. doi: 10.1088/0305-4470/34/20/302 [8] A. H. Arnous, M. Ekici, S. P. Moshokoa, et al., Solitons in nonlinear directional couplers with optical metamaterials by trial function scheme, Acta Phys. Polonica A., 2017, 132(4), 1399–1410. doi: 10.12693/APhysPolA.132.1399 [9] A. Biswas, M. A. Ekici, Sonmezoglu, et al., Solitons in optical metamaterials with anti-cubic nonlinearity, Eur. Phys. J. Plus, 2018, 133, 204. doi: 10.1140/epjp/i2018-12046-6 [10] A. Biswas, K. R. Khan, M. F. Mahmood, et al., Bright and dark solitons in optical metamaterials, Optik, 2014, 125, 3299–3302 doi: 10.1016/j.ijleo.2013.12.061 [11] A. Biswas, M. Mirzazadeh, M. Eslami, et al., Solitons in optical metamaterials by functional variable method and first integral approach, Frequenz, 2014, 68(11–12), 525–530. [12] P. F. Byrd and M. D. Fridman, Handbook of Elliptic Integrals for Engineers and Sciensists, Springer, Berlin, 1971. [13] M. Ekici, Exact solitons in optical metamaterials with quadratic-cubic nonlinearity using two integration approaches, Optik, 2018, 156, 351–355. doi: 10.1016/j.ijleo.2017.11.056 [14] M. Ekici, A. Sonmezoglu, Q. Zhou, et al., Analysis of optical solitons in nonlinear negative-indexed materials with anti-cubic nonlinearity, Opt. Quantum Electron., 2018, 50(2), 75. doi: 10.1007/s11082-018-1341-3 [15] S. Y. Elnaggar and G. N. Milford, Description and stability analysis of nonlinear transmission line type metamaterials using nonlinear dynamics theory, J. Appl. Phys., 2017, 121(12), 124902. doi: 10.1063/1.4979022 [16] M. Foroutan, J. Manafian and A. Ranjbaran, Solitons in optical metamaterials with anti-cubic law of nonlinearity by generalized G′/G-expansion method, Optik, 2018, 162, 86–94. doi: 10.1016/j.ijleo.2018.02.087 [17] M. Foroutan, J. Manafian and I. Zamanpour, Solitonwave solutions in optical metamaterials with anti-cubic law of nonlinearity by ITEM, Optik, 2018, 164, 371–379. doi: 10.1016/j.ijleo.2018.03.025 [18] Y. Fu and J. Li, Exact stationary-wave solutions in the standard model of the Kerr-nonlinear optical fiber with the bragg grating, J. Appl. Anal, Comput., 2017, 7(3), 1177–1184. [19] A. A. Kader, M. A. Latif and Q. Zhou, Exact optical solitons in metamaterials with anti-cubic law of nonlinearity by Lie group method, Opt. Quantum Electron, 2019, 51(1), 30. doi: 10.1007/s11082-019-1748-5 [20] E. Krishnan, M. Al Gabshi, Q. Zhou, et al., Solitons in optical metamaterials by mapping method, Optoelectron. Adv. Mater. Commun., 2015, 17, 511–516. [21] E. Krishnan, A. Biswas, Q. Zhou, et al., Optical solitons with anti-cubic nonlinearity by mapping methods, Optik, 2018, 170, 520–526. doi: 10.1016/j.ijleo.2018.06.010 [22] M. Lapine, M. Gorkunov and K. H. Ringhofer, Nonlinearity of a metamaterial arising from diode insertions into resonant conductive elements, Phys. Rev. E., 2003, 67, 065601. [23] J. Li, Geometric properties and exact travelling wave solutions for the generalized Burger-Fisher equation and the Sharma-Tasso-Olver equation, J. Nonl. Mod. Anal., 2019, 1(1), 1–10. [24] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [25] J. Li and G. Chen, Bifurcations of travelling wave solutions for four classes of nonlinear wave equations, Int. J. Bifurcat. Chaos, 2005, 15(12), 3973–3998. doi: 10.1142/S0218127405014416 [26] J. Li and G. Chen, On a class of singular nonlinear traveling wave equations, Int. J. Bifurcat. Chaos, 2007, 17(11), 4049–4065. doi: 10.1142/S0218127407019858 [27] J. Li and M. Han, Exact peakon solutions given by the generalized hyperbolic functions for some nonlinear wave equations, J. Appl. Anal, Comput., 2020, 10(4), 1708–1719. [28] J. Li, Y. Zhang and X. Zhao, On a class of singular nonlinear traveling wave equations (Ⅱ): an example of GCKdV equations, Int. J. Bifurcat. Chaos, 2011, 19(6), 1955–2007. [29] N. N. Potravkin, V. A. Makarov and I. A. Perezhogin, Modeling highly-dispersive transparency in planar nonlinear metamaterials, Opt. Commun., 2017, 385, 177–180. doi: 10.1016/j.optcom.2016.10.056 [30] E. Prati, Microwave propagation in round guiding structures based on double negative metamaterials, Int. J. Infrared Milli., 2006, 27(9), 1227–1239. [31] R. A. Shelby, D. R. Smith and S. Schultz, Experimental Verification of a Negative Index of Refraction, Science, 2001, 292(5514), 77–79. doi: 10.1126/science.1058847 [32] H. Triki, A. Biswas, Q. Zhou, et al., Solitons in optical metamaterials having parabolic law nonlinearity with detuning effect and Raman scattering, Optik, 2018, 164, 606–609. doi: 10.1016/j.ijleo.2018.03.068 [33] R. Yang and I. V. Shadrivov, Double-nonlinear metamaterials, Appl. Phys. Lett., 2010, 97(23), 231114. doi: 10.1063/1.3525172 [34] E. Zayed and K. Alurrfi, New extended auxiliary equation method and its applications to nonlinear Schrödinger-type equations, Optik, 2016, 127, 9131–9151. doi: 10.1016/j.ijleo.2016.05.100 [35] X. Zeng and X. Yong, A new mapping method and its applications to nonlinear partial differential equations, Phys. Lett. A, 2008, 372(44), 6602–6607. doi: 10.1016/j.physleta.2008.09.025 [36] Q. Zhang, Bifurcations and exact solutions of the optical soliton model in metamaterials dominated by anti-cubic nonlinearity, J. Appl. Anal. Comput., 2022, 12(4), 1517–1531. [37] A. A. Zharov, I. V. Shadrivov and Y. S. Kivshar, Nonlinear Properties of Left-Handed Metamaterials, Phys. Rev. Lett., 2003, 91, 037401. doi: 10.1103/PhysRevLett.91.037401 [38] Y. Zhou and J. Zhuang, Bifurcations and exact eolutions of the Raman soliton model in nanoscale optical waveguides with metamaterials, J. Nonl. Mod. Anal., 2021, 3(1), 145–165. [39] B. Zheng, A new Bernoulli sub-ODE method for constructing traveling wave solutions for two nonlinear equations with any order, U. Politeh. Buch. Ser. A., 2011, 73(3), 85–94. -
-
-
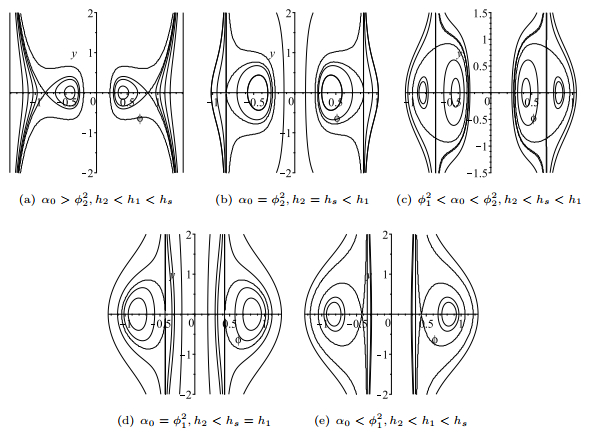
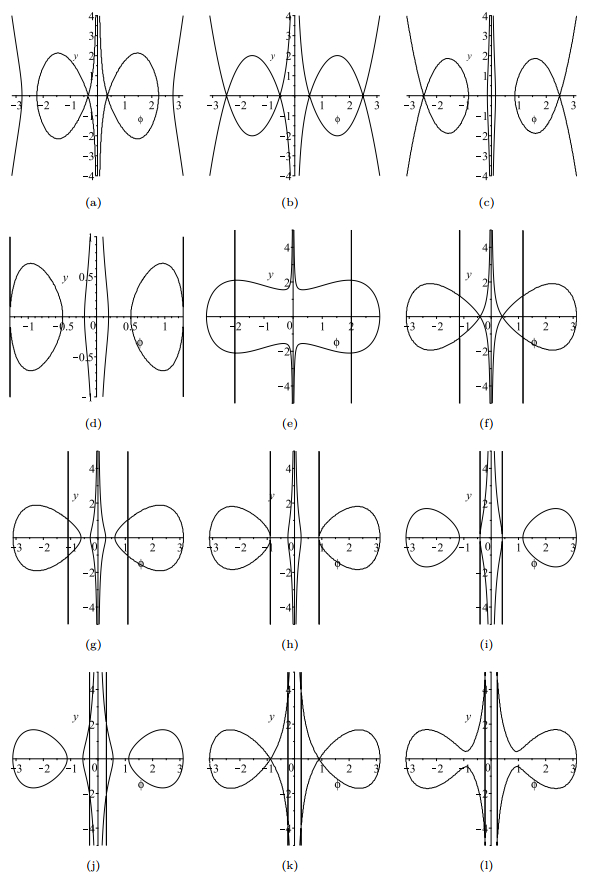
Figure 1.
The phase portraits of system (1.5) when
$ \alpha_0 $ -
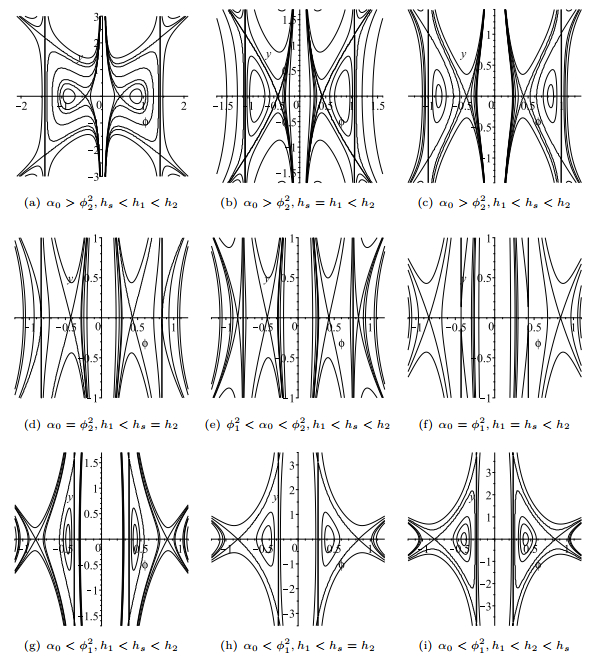
Figure 2.
The phase portraits of system (1.5) when
$ \alpha_0 $ -
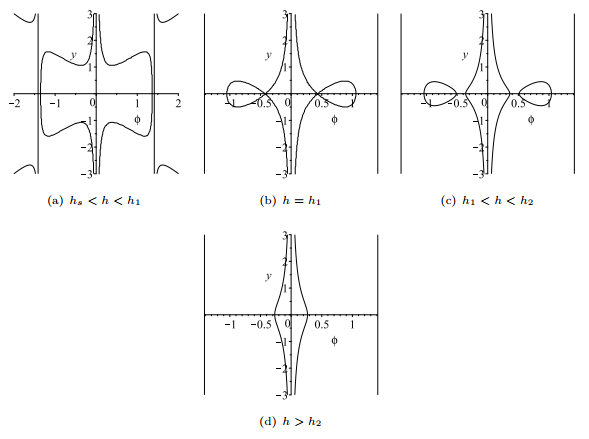
Figure 3.
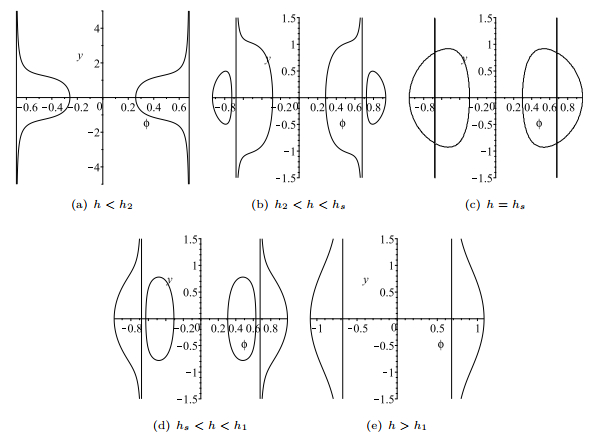
The changes of the level curves
$ H(\phi, y)=h $ -
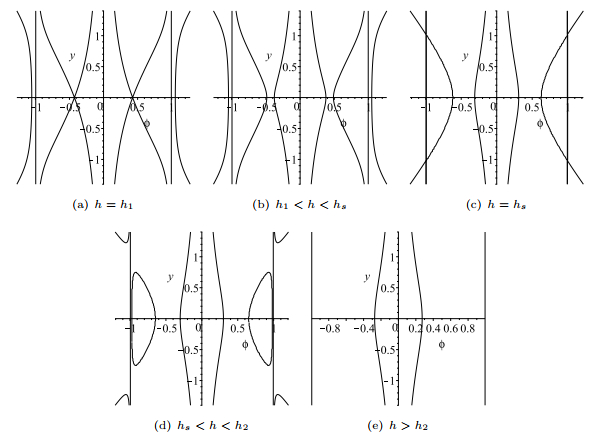
Figure 4.
The changes of the level curves
$ H(\phi, y)=h $ -
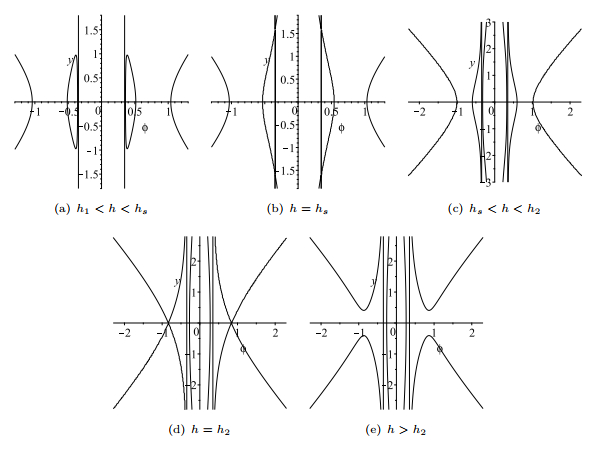
Figure 5.
The changes of the level curves
$ H(\phi, y)=h $ -
Figure 6.
The changes of the level curves
$ H(\phi, y)=h $ -
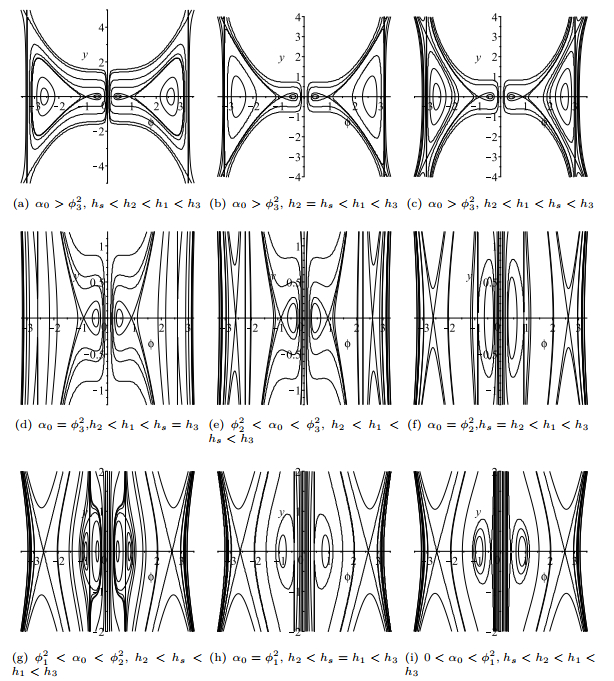
Figure 7.
The phase portraits of system (1.7) as
$ \alpha_0 $ -
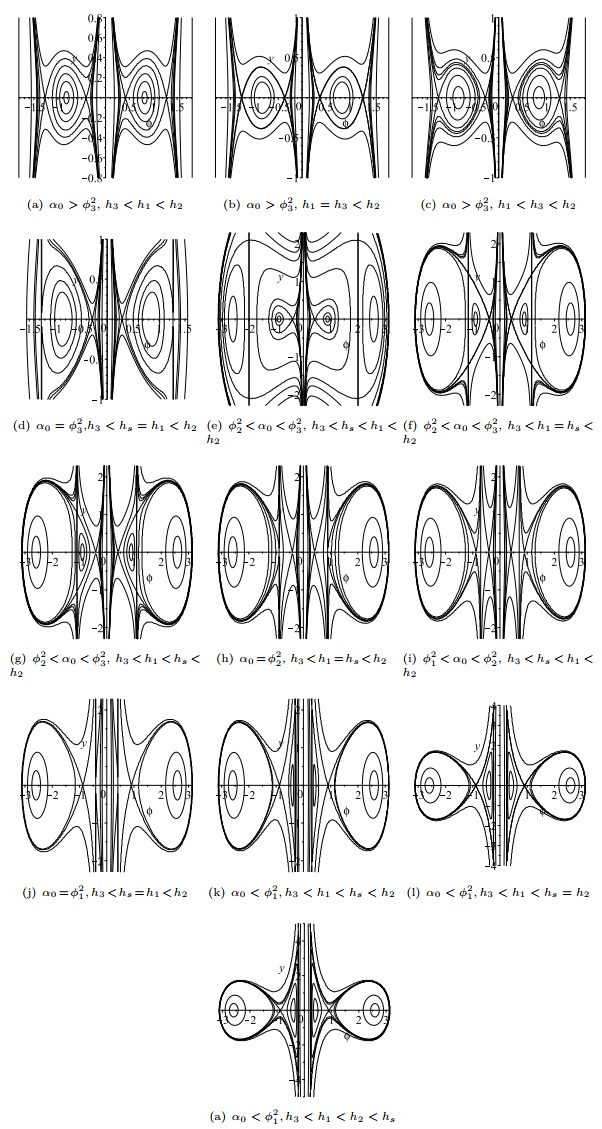
Figure 8.
The phase portraits of (1.7) as
$ \alpha_0 $ -
Figure 9.
The changes of the level curves
$ H(\phi, y)=h $ -
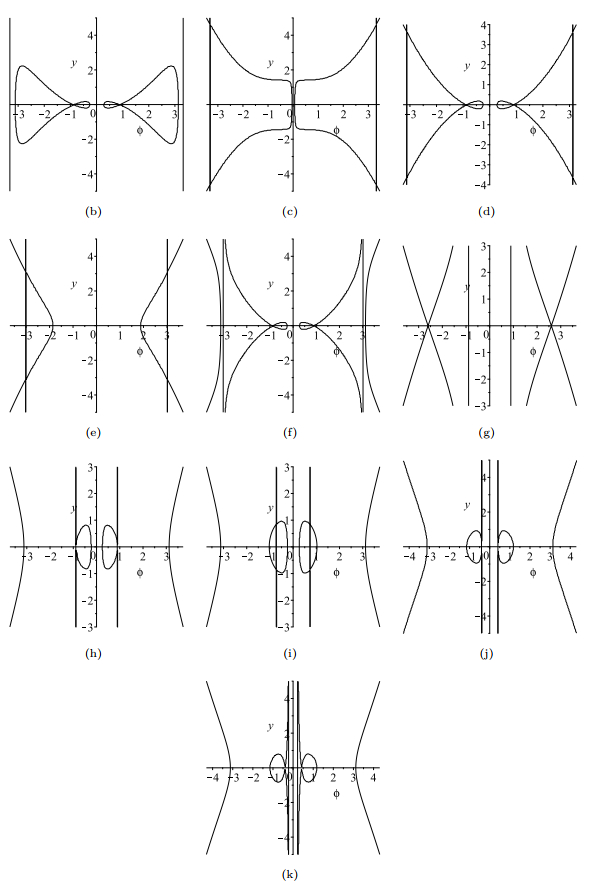
Figure 10.
The changes of the level curves
$ H(\phi, y)=h $




 DownLoad:
DownLoad: