| Citation: | Xin Li, Fazhan Geng. BOUNDARY LAYER-PRESERVING METHODS FOR A CLASS OF NONLINEAR SINGULAR PERTURBATION BOUNDARY VALUE PROBLEMS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1972-1982. doi: 10.11948/20220310 |
BOUNDARY LAYER-PRESERVING METHODS FOR A CLASS OF NONLINEAR SINGULAR PERTURBATION BOUNDARY VALUE PROBLEMS
-
Abstract
The aim of this paper is to develop a new uniformly convergent numerical approach for nonlinear singularly perturbed boundary value problems (BVPs). The method combines the advantages of the variation-of-constants formula and the reproducing kernel function approximation. It can preserve the boundary layer structure of the solution to the considered singular perturbation problems. In addition, compared with some existing numerical techniques, the present method has no restriction on the choice of nodes. Three numerical experiments are implemented and the numerical results indicate our new technique is quite promising.
-

-
References
[1] T. Allahviranloo and H. Sahihi, Reproducing kernel method to solve fractional delay differential equations, Appl. Math. Comput., 2021, 400, 126095. [2] O. Abu Arqub and B. Maayah, Modulation of reproducing kernel Hilbert space method for numerical solutions of Riccati and Bernoulli equations in the Atangana-Baleanu fractional sense, Chaos Solitons Fractals, 2019, 125, 163-170. doi: 10.1016/j.chaos.2019.05.025 [3] A. Alvandi and P. Paripour, The combined reproducing kernel method and Taylor series for handling nonlinear Volterra integro-differential equations with derivative type kernel, Appl. Math. Comput., 2019, 355, 151-160. [4] A. Akgül, A novel method for a fractional derivative with non-local and non-singular kernel, Chaos Solitons Fractals, 2018, 114, 478-482. doi: 10.1016/j.chaos.2018.07.032 [5] M. Al-Smadi and O. Abu Arqub, Computational algorithm for solving fredholm time-fractional partial integrodifferential equations of dirichlet functions type with error estimates, Appl. Math. Comput., 2019, 342, 280-294. [6] M. Cui and Y. Lin, Nonlinear numerical analysis in reproducing kernel space, Nova Science Pub Inc, Hauppauge, 2009. [7] F. Geng and M. Cui, Solving a nonlinear system of second order boundary value problems, J. Math. Anal. Appl., 2007, 327, 1167-1181. doi: 10.1016/j.jmaa.2006.05.011 [8] F. Geng and S. Qian, Reproducing kernel method for singularly perturbed turning point problems having twin boundary layers, Appl. Math. Lett., 2013, 26, 998-1004. doi: 10.1016/j.aml.2013.05.006 [9] F. Geng and S. Qian, Modified reproducing kernel method for singularly perturbed boundary value problems with a delay, Appl. Math. Model., 2015, 39, 5592-5597. doi: 10.1016/j.apm.2015.01.021 [10] F. Geng and S. Qian, A new numerical method for singularly perturbed turning point problems with two boundary layers based on reproducing kernel method, Calcolo, 2017, 54, 515-526. doi: 10.1007/s10092-016-0196-x [11] F. Geng, Numerical methods for solving Schröinger equations in complex reproducing kernel Hilbert spaces, Mathematical Sciences, 2020, 14, 293-299. doi: 10.1007/s40096-020-00337-6 [12] Y. Gao, X. Li and B. Wu, A continuous kernel functions method for mixed-type functional differential equations, Mathematical Sciences. DOI: 10.1007/s40096-021-00409-1. [13] F. T. Isfahani, R. Mokhtari, G. B. Loghmani and M. Mohammadi, Numerical solution of some initial optimal control problems using the reproducing kernel Hilbert space technique, International Journal of Control, 2020, 93, 1345-1352. doi: 10.1080/00207179.2018.1506888 [14] W. Jiang, Z. Chen and N. Hu, Multi-scale orthogonal basis method for nonlinear fractional equations with fractional integral boundary value conditions, Appl. Math. Comput., 2020, 378, 125151. [15] A. Kaushik, V. Kumar and A. K. Vashishth, An efficient mixed asymptotic-numerical scheme for singularly perturbed convection diffusion problems, Appl. Math. Comput., 2012, 218, 8645-8658. [16] M. K. Kadalbajoo and P. Arora, B-spline collocation method for the singular-perturbation problem using artificial viscosity, Comput. Math. Appl., 2009, 57, 650-663. [17] M. K. Kadalbajoo and D. Kumar, Initial value technique for singularly perturbed two point boundary value problems using an exponentially fitted finite difference scheme, Comput. Math. Appl., 2009, 57, 1147-1156. [18] M. K. Kadalbajoo, P. Arora and V. Gupta, Collocation method using artificial viscosity for solving stiff singularly perturbed turning point problem having twin boundary layers, Comput. Math. Appl., 2011, 61, 1595-1607. [19] X. Li and B. Wu, Error estimation for the reproducing kernel method to solve linear boundary value problems, J. Comput. Appl. Math., 2013, 243, 10-15. doi: 10.1016/j.cam.2012.11.002 [20] P. Rai and K. K. Sharma, Numerical study of singularly perturbed differential-difference equation arising in the modeling of neuronal variability, Comput. Math. Appl., 2012, 63, 118-132. [21] P. Rai and K. K. Sharma, Numerical approximation for a class of singularly perturbed delay differential equations with boundary and interior layer(s), Numer. Algor, 2019. https://doi.org/10.1007/s11075-019-00815-6. [22] H. G. Roos, M. Stynes and L. Tobiska, Robust Numerical Methods for Singularly Perturbed Differential Equations, Springer, 2008. [23] H. Sahihi, S. Abbasbandy and T. Allahviranloo, Computational method based on reproducing kernel for solving singularly perturbed differential-difference equations with a delay, Appl. Math. Comput., 2019, 361, 583-598. [24] G. I. Shishkin and L. P. Shishkina, Difference methods for singular perturbation problems, Taylor and Francis, 2009. [25] H. Sahihi, T. Allahviranloo and S. Abbasbandy, Solving system of second-order BVPs using a new algorithm based on reproducing kernel Hilbert space, Appl. Numer. Math., 2020, 151, 27-39. [26] H. Wendland, Scattered data approximation, Cambridge University Press, New York, 2004. [27] Y. Zhang, Y. Lin and Y. Shen, A new multiscale algorithm for solving second order boundary value problems, Appl. Numer. Math., 2020, 156, 528-541. -
-
-
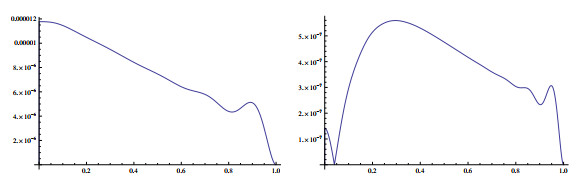
Figure 1.
Exact solution (left) and absolute error (right) for
$ \varepsilon=10^{-3} $ -
Figure 2.
Absolute errors for
$ \varepsilon=10^{-9} $ $ N=20 $ $ N=40 $ -
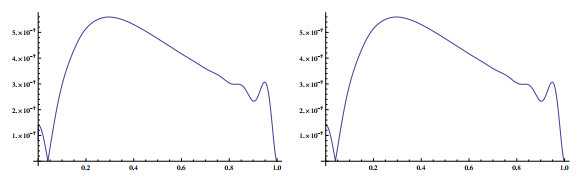
Figure 3.
Absolute errors for
$ \varepsilon=10^{-5} $ $ N=10 $ $ N=20 $ -
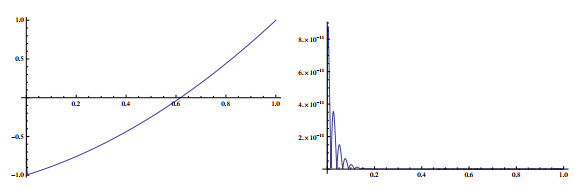
Figure 4.
Absolute errors for
$ \varepsilon=10^{-7} $ $ \varepsilon=10^{-9} $ $ N=20 $




 DownLoad:
DownLoad: