| Citation: | Pius W. M. Chin. THE EFFECT ON THE SOLUTION OF THE FITZHUGH-NAGUMO EQUATION BY THE EXTERNAL PARAMETER $\alpha$ USING THE GALERKIN METHOD[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1983-2005. doi: 10.11948/20220316 |
THE EFFECT ON THE SOLUTION OF THE FITZHUGH-NAGUMO EQUATION BY THE EXTERNAL PARAMETER $\alpha$ USING THE GALERKIN METHOD
-
Abstract
The Fitzhugh-Naguno equation is one of the most popular and attractive equation in real life. This equation is applicable in many different areas of physics, biology, population genetics and applied sciences to mention a few. In this paper, we design and analyze a coupled scheme consisting of the non-standard finite difference and the Galerkin methods in both time and space variables respectively. We show analytically by the use of the Galerkin method and the compactness theorem that the solution of this equation exists uniquely in appropriate spaces with the parameter $\alpha$ that determines the main dynamics of the equation, under controlled. We further show numerically that the above scheme is stable and converge optimally in specified norms with its numerical solution replicating the qualitative properties of the exact solution. We finally present numerical experiments with the help of an example and a careful choice of $\alpha$ to validate the theoretical results.
-

-
References
[1] S. Abbasbandy, Soliton solutions for the Fitzhugh-Nagumo equation with the homotophy analysis method, Applied Mathematical Modeling, 2008, 32, 2706-2714. doi: 10.1016/j.apm.2007.09.019 [2] A. R. Adams, Sobolev Space, Academic Press, New York, 1975. [3] A. A. Aderogha and M. Chapwanya, An explicit nonstandard finite difference scheme for the Allen-Cahn equation, Journal of Difference Equations and Applications, 2015, 21(10), 875-886. doi: 10.1080/10236198.2015.1055737 [4] J. G. Alford, Bifurcation structure of rotating wave solutions of the Fitzhugh-Nagumo equations, Communications in Nonlinear Science and Numerical Simulation, 2009, 14, 3282-3291. doi: 10.1016/j.cnsns.2009.01.011 [5] R. Anguelov and J. M. S. Lubuma, Contributions to the mathematics of the nonstandard finite difference method and applications, Numerical Methods for Partial Differential Equations, 2001, 17(5), 518-543. doi: 10.1002/num.1025 [6] R. Anguelov and J. M. S. Lubuma, Nonstandard finite difference method by nonlocal approximation, Mathematics and Computers in Simulation, 2003, 61(3), 465-475. [7] D. G. Aronson and H. F. Weinberger, Multidimensional nonlinear diffusion arising in population genetics, Advances in Mathematics, 1978, 30, 33-76. doi: 10.1016/0001-8708(78)90130-5 [8] J. P. Aubin, Un théoréme de compacité, C. R. Acad. Sc. Paris, 1963, 256, 5012-5014. [9] P. W. M. Chin, Optimal Rate of Convergence for a Nonstandard Finite Difference Galerkin Method Applied to Wave Equation Problems, Journal of Applied Mathematics, 2013. [10] P. W. M. Chin, J. K. Djoko and J. M. S. Lubuma, Reliable numerical schemes for a linear diffusion equation on a nonsmooth domain, Applied Mathematics Letters, 2010, 23(5), 544-548. doi: 10.1016/j.aml.2010.01.008 [11] P. W. M. Chin, The Galerkin reliable scheme for the numerical analysis of the Burgers'-Fisher equation, Progress in Computational Fluid Dynamics, 2021, 21(4), 234-247. doi: 10.1504/PCFD.2021.116530 [12] P. W. M. Chin, The study of the numerical treatment of the Real Ginzburg-Landau equation using the Galerkin method, Numerical Functional Analysis and Optimization, 2021, 42(10), 1154-1177. DOI: 10.1080/016305632021.1948863. [13] P. G. Ciarlet, The finite element method for elliptic problems, Elsevier, 1978. [14] L. C. Evan, Partial Differential Equations. Graduate, Studies in Mathematics, American Mathematical Society, Rhode Island, 1998, 19. [15] R. Fitzhugh, Impulse and physiological states in theoretical models of nerve membrane, Biophysical Journal, 1961, 1(6), 445-466. doi: 10.1016/S0006-3495(61)86902-6 [16] A. Hodgkin and A. Huxley, A quanlitative description of membrane current and its application to conduction and excitation in nerve, The Journal of Physiology, 1952, 117(4), 500. doi: 10.1113/jphysiol.1952.sp004764 [17] S. Hussain, N. Malluwawadu and P. Zhu, A weak Galerkin finite element method for the second order elliptic problem with mixed boundary conditions, Journal of Applied Analysis and Computation, 2018, 8(5), 1452-1463. DOI: 10.11948/2018.1452. [18] D. E. Jackson, Existence and regularity of the Fitzhugh-Nagumo equations, Nonlinear Analysis: Real World Applications, 2002, 3, 515-541. doi: 10.1016/S1468-1218(01)00046-3 [19] D. E. Jackson, Error estimates for the semi-discrete Galerkin approximation of the Fitzhugh-Nagumo equations, Appl. Math. Comput., 1992, 50, 93-114. [20] C. Johnson, S. Larsson, V. Thomée and L. B. Wahlbin, Error estimates for spatially discrete approximations of semilinear parabolic equations with nonsmooth initial data, Mathematics of Computation, 1987, 180, 331-357. [21] M. M. Khader and K. M. Abualnaja, Galerkin-FEM for obtaining the numerical solution of the linear fractional Klein-Gorden equation, Journal of Applied Analysis and Computation, 2019, 9(1), 261-270. doi: 10.11948/2019.261. [22] T. Kawahara and M. Tanaka, Interaction of travelling fronts: an exact solution of a nonlinear diffusion equation, Physics Letters A., 1983, 97, 311-314. doi: 10.1016/0375-9601(83)90648-5 [23] H. Li and Y. Guo, New exact solutions to the Fitzhugh-Nagumo equation, Applied Mathematics and Computation, 2006, 180, 524-528. doi: 10.1016/j.amc.2005.12.035 [24] J. L. Louis, E. Magenes and P. Kenneth, Non-homogeneous Boundary Value Problems and Applications, Springer Berlin, 1972, 1. [25] J. M. S. Lubuma. E. Mureithi and Y. A. Terefe, Analysis and dynamically consistent numerical scheme for the SIS model and related reaction diffusion equation, AIP Conf. Proc., 2011, 168. [26] J. M. S. Lubuma, E. Mureithi and Y. A. Terefe, Nonstandard discretization of the SIS Epidemiological model with and without diffusion, Contemporary Mathematics, 2014, 618. [27] R. E. Mickens, Nonstandard finite difference models of differential equations, World Scientific, 1994. [28] S. M. Moghadas, M. E. Alexander, B. D. Corbett and A. B. Gumel, A positivity-preserving Mickens-type discretization of an epidemic model, The Journal of Difference Equations and Applications, 2003, 9(11), 1037-1051. doi: 10.1080/1023619031000146913 [29] J. Nagumo, S. Arimoto and S. Yoshizawa, An active pulse transmission line simulating nerve axon, Proceedings of the IRE, 1962, 50(10), 2061-2070. doi: 10.1109/JRPROC.1962.288235 [30] J. Nagumo, S. Yoshizawa and S. Arimoto, Bistable transmission lines, Transactions on IEEE Circuit Theory, 1965, 12, 400-412. doi: 10.1109/TCT.1965.1082476 [31] M. C. Nucci and P. A. Clarkson, The nonclassical method is more general than the direct method for symmetry reductions: an example of the Fitzhugh-Nagumo equation, Physics Letters A, 1992, 164, 49-56. doi: 10.1016/0375-9601(92)90904-Z [32] K. C. Partida, On the use of nonstandard finite difference methods, Journal of Difference Equations and Applications, 2005, 11(8), 735-758. doi: 10.1080/10236190500127471 [33] W. Rudin, Functional Analysis, McGraw-Hill, New York, 1991. [34] S. Singh, Mixed-type discontinuous Galerkin approach for solving the generalized Fitzhugh-Nagumo reaction-diffusion model, Int. J. Appl. Comput. Math., 2021, 7, 207. doi. org/10.1007/s40819-021-01153-9. doi: 10.1007/s40819-021-01153-9 [35] A. C. Scott, Neustor propagation on a tunnel diode loaded transmission line, Proceedings of IEEE, 1963, 51, 240-249. doi: 10.1109/PROC.1963.1715 [36] J. Shen, Long time stability and convergence for the fully discrete nonlinear Galerkin methods, Appl. Anal., 1990, 38, 201-229. doi: 10.1080/00036819008839963 [37] M. Shih. E. Momoniat and F. M. Mahomed, Approximate conditional symmetries and approximate solutions of the perturbed Fitzhugh-Nagumo equation, Journal of Mathematical Physics, 2005, 46, 023503. doi: 10.1063/1.1839276 [38] K. Takashi, The sub-supersolution method for the Fitzhugh-Nagumo type reaction-diffusion system with heterogeneity, Discrete and Continuous Dynamical System, 2018, 38(5), 2441-2465. doi: 10.3934/dcds.2018.101. [39] R. Temam, Navier-Stokes Equations: Theory and Numerical Analysis, Amsterdam, North-Holland, 1984. [40] R. Temam, Infinite Dimensional Dynamical System in Mechanics and Physics, Springer-Verlag, New York, 1997. [41] R. A. Van Gorder, A variational formulation of the Nagumo reaction-diffusion equation and the Nagumo telegraph equation, Nonlinear Anal. Real World Appl., 2010, 11, 2957-2962. doi: 10.1016/j.nonrwa.2009.10.016 [42] B. van der Pol. and J. van der Mark, The heartbeat considered as a relaxation oscillation and an electrical model of the heart, In Philosophical Magazine series, 1928, 7(6), 763-775. [43] M. F. Wheeler, A priori $L^{2}$ error estimates for Galerkin approximations to parabolic partial differential equations, SIAM J. Numer. Anal., 1973, 10, 723-759. doi: 10.1137/0710062 [44] W. Zhao and A. Gu, Regularity of pullback attractors and random equilibrium for non-autonomous system stochastic Fitzhugh-Nagumo system on unbounded domain, Journal of Applied Analysis and Computation, 2017, 7(4), 1285-1311. doi: 10.1948/2017.079. -
-
-
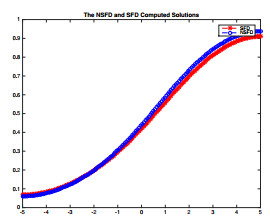
Figure 1.
Exact solution of the NSFD and SFD-GM Schemes
-
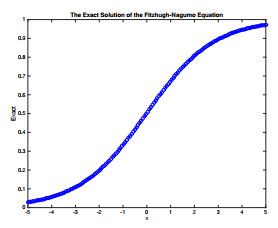
Figure 2.
Approximate solution for NSFD and SFD- GM Schemes
-
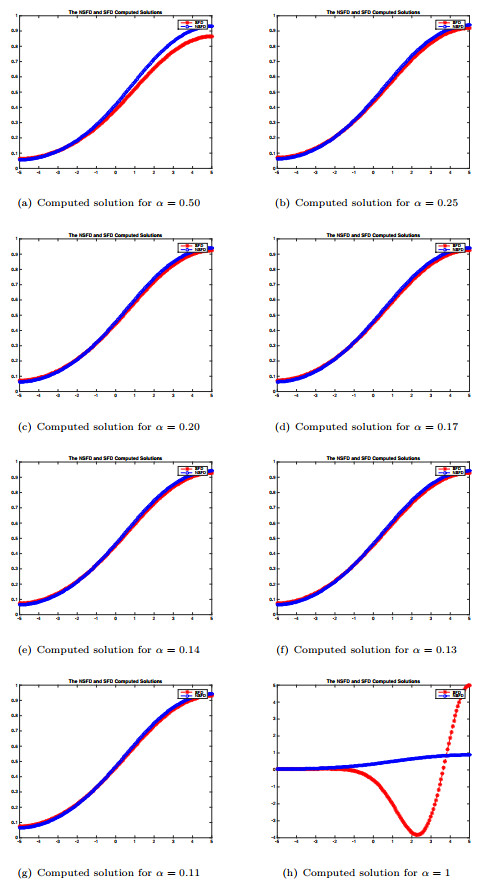
Figure 3.
The Effect of
$ \alpha $




 DownLoad:
DownLoad: