| Citation: | Peiting Gao, Wen Zheng, Tao Wang, Yifei Li, Futong Li. SIGNAL RECOVERY WITH CONSTRAINED MONOTONE NONLINEAR EQUATIONS THROUGH AN EFFECTIVE THREE-TERM CONJUGATE GRADIENT METHOD[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2006-2025. doi: 10.11948/20220335 |
SIGNAL RECOVERY WITH CONSTRAINED MONOTONE NONLINEAR EQUATIONS THROUGH AN EFFECTIVE THREE-TERM CONJUGATE GRADIENT METHOD
-
Abstract
In this paper, we introduce a three-term conjugate gradient-type projection method for solving constrained monotone nonlinear equations. In this method, we firstly undertake the transformation of the relative matrices proposed by Yao and Ning. Secondly, we obtain the new relative matrices involving two parameters. Subsequently, we construct a relationship for the two parameters via the quasi-Newton equation and obtain the parameters by simplifying maximum eigenvalue of the new relative matrices. Finally, combining the three-term conjugate gradient method with projection technique, we establish an efficient three-term conjugate gradient-type projection algorithm. Meanwhile, we also give some theoretical analysis about the global convergence and R-linear convergence of the proposed algorithm under quite reasonable technical assumptions. Performance comparisons show that our proposed method is competitive and efficient for solving large-scale nonlinear monotone equations with convex constraints. Furthermore, the presented algorithm is also applied to recovery of a sparse signal in compressive sensing, and obtain practical, efficient and competitive performance in comparing with state-of-the-art algorithms.
-

-
References
[1] N. Andrei, A double parameter scaled BFGS method for unconstrained optimization, J. Comput. Appl. Math., 2018, 332, 26-44. doi: 10.1016/j.cam.2017.10.009 [2] E. J. Candes, J. K. Romberg and T. Tao, Stable signal recovery from incomplete and inaccurate measurements, Pure Appl. Math., 2006, 59, 1207-1223. doi: 10.1002/cpa.20124 [3] E. D. Dolan and J. J. Morè, Benchmarking Optimization Sofeware with performance profiles, Math. Program, 2002, 91, 201-213. doi: 10.1007/s101070100263 [4] P. Gao, C. He and Y. Liu, An adaptive family of projection methods for constrained monotone nonlinear equations with applications, Appl. Math. Comput., 2019, 359, 1-16. doi: 10.1016/j.cam.2019.03.025 [5] P. Gao, T. Wang, X. Liu and Y. Wu, An effificient three-term conjugate gradient-based algorithm involving spectral quotient for solving convex constrained monotone nonlinear equations with applications, Comput. Appl. Math., 2022. Doi: 10.1007/s40314-022-01796-4. [6] P. Gao and C. He, An efficient three-term conjugate gradient method for nonlinear monotone equations with convex constraints, Calcolo, 2018. Doi: 10.1007/s10092-018-0291-2. [7] A. S. Haliu, A. Majumder, M. Y. Waziri and K. Ahmed, Signal recovery with convex constrained nonlinear monotone equations through conjugate gradient hybrid approach, Math. Comput. Simulat., 2021, 187, 520-539. doi: 10.1016/j.matcom.2021.03.020 [8] J. Liu, Z. Lu, J. Xu, S. Wu and Z. Tu, An efficient projection-based algorithm without Lipschitz continuity for large-scale nonlinear pseudo-monotone equations, J. Comput. Appl. Math., 2022, 403, 113822. doi: 10.1016/j.cam.2021.113822 [9] J. Pang, inext newton methods for the nonlinear complementary problem, Math. Program, 1986, 36, 54-71. doi: 10.1007/BF02591989 [10] W. Sun and X. Yuan, Optimization Theory and methods, Nonlinear Program, Springer Science+business Media, New York, 2005. [11] M. V. Solodov and B. F. Svaiter, Reformulation: nonsmooth, piecewise smooth, semismooth and smoothing methods, In: Fukushima, M., Qi, L. (eds. ) A globally convergent inexact Newton method for systems of monotone equations, Dordrecht: Kluwer Academic Publishers, 1998, 355-369. [12] C. Wang, Y. Wang and C. Xu, A projection method for a system of nonlinear monotone equations with convex constraints, Math. Methods Oper. Res., 2007, 66, 33-46. doi: 10.1007/s00186-006-0140-y [13] M. Y. Waziri, K. Ahmed, A. S. Halilu and J. Sabi'u, Two new Hager-Zhang iterative schemes with improved parameter choices for monotone nonlinear systems and their applications in compressed sensing, Rairo-Oper. Res., 2021. Doi: 10.1051/ro/2021190. [14] M. Y. Waziri, K. Ahmed and J. Sabi'u, A family of Hager-Zhang conjugate gradient methods for system of monotone nonlinear equations, Appl. Math. Comput., 2019, 361, 645-660. [15] M. Y. Waziri, K. Ahmed and J. Sabi'u, A Dai-Liao conjugate gradient method via modified secant equation for system of nonlinear equations, Arab. J. Math., 2020, 9, 443-457. doi: 10.1007/s40065-019-0264-6 [16] M. Y. Waziri, K. Ahmed and J. Sabi'u, Descent Perry conjugate gradient methods for systems of monotone nonlinear equations, Numer. Algorithems, 2020, 85, 763-785. doi: 10.1007/s11075-019-00836-1 [17] Y. Xiao, Q. Wang and Q. Hu, Non-smooth equations based method for $l_1$-norm problems with applications to compressed sensing, Nonlinear Anal., 2011, 74, 3570-3577. doi: 10.1016/j.na.2011.02.040 [18] S. Yao and L. Ning, An adaptive three-term conjugate gradient method based on self-scaling memoryless BFGS matrix, J. Comput. Appl. Math., 2018, 332, 72-85. doi: 10.1016/j.cam.2017.10.013 [19] J. Yin, J. Jian and X. Jiang, A hybrid three-term conjugate gradient projection method for constrained nonlinear monotone equations with applications, Numer. Algorithms, 2021, 88, 389-418. doi: 10.1007/s11075-020-01043-z [20] J. Yin, J. Jian and X. Jiang, A generalized hybrid CGPM-based algorithm for solving large-scale convex constrained equations with applications to image restoration, J. Comput. Appl. Math., 2021, 391, 113423. doi: 10.1016/j.cam.2021.113423 [21] W. Zhou and D. Li, A globally convergent BFGS method for nonlinear monotone equations without any merit functions, Math. Comput., 2008, 77, 2231-2240. doi: 10.1090/S0025-5718-08-02121-2 -
-
-
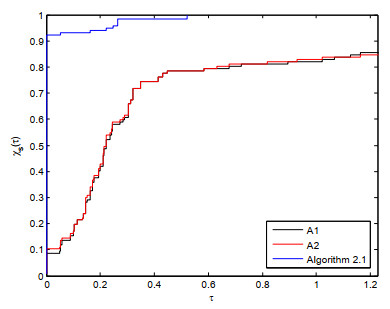
Figure 1.
Performance profiles of three algorithms with respect to the CPU time.
-
Figure 2.
Performance profiles of three algorithms with respect to the number of iteration.
-
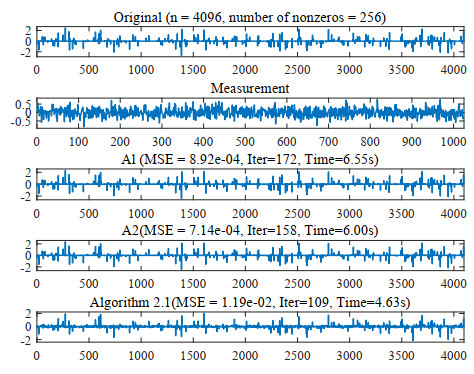
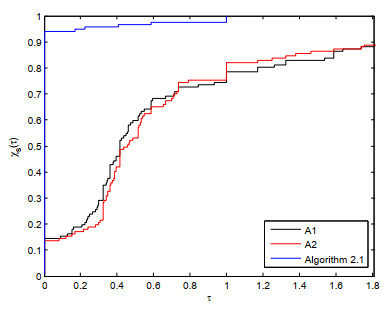
Figure 3.
From top to bottom: the original signal, the measurements, and the reconstructed signals by three algorithms.
-
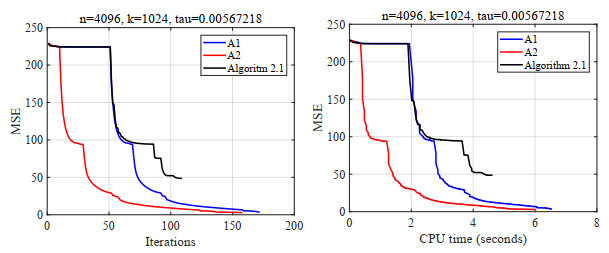
Figure 4.
Plots of MSE versus iteration and time.
-
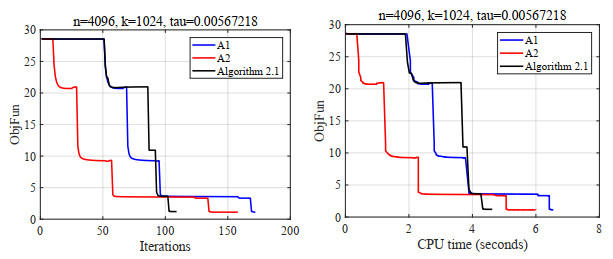
Figure 5.
Plots of objective function value versus iteration and time.




 DownLoad:
DownLoad: