| Citation: | Jun Qian, Youhui Su, Xiaoling Han, Yongzhen Yun. STABILITY AND EXISTENCE OF SOLUTIONS FOR A COUPLED SYSTEM OF FRACTIONAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2026-2047. doi: 10.11948/20220336 |
STABILITY AND EXISTENCE OF SOLUTIONS FOR A COUPLED SYSTEM OF FRACTIONAL DIFFERENTIAL EQUATIONS
-
Abstract
In this paper, we study a coupled system of Caputo type fractional differential equations with integral boundary conditions. By Leray-Schauder alternative theorem, the existence of solutions for the factional differential system are obtained. The Hyers-Ulam stability of solutions is discussed and sufficient conditions for the stability are developed. The main results are well illustrated with examples and numerical simulation graphs. The interesting point of this article is that it not only gives approximate graphs of solution by using the iterative methods, but also verifies the Hyers-Ulam stability of the coupling system by numerical simulation.
-

-
References
[1] R. P. Agarwal and S. Heikkila, On the solvability of first-order discontinuous scalar initial and boundary value problems, Anziam. J., 2003, 44(4), 513-538. doi: 10.1017/S1446181100012906 [2] B. Ahmad, S. K. Ntouyas and A. Alsaedi, On a coupled system of fractional differential equations with coupled nonlocal and integral boundary conditions, Chaos. Soliton. Fract., 2016, 83, 234-241. doi: 10.1016/j.chaos.2015.12.014 [3] A. Alkhazzan, P. Jiang, D. Baleanu, et al, Stability and existence results for a class of nonlinear fractional differential equations with singularity, Math. Method. Appl. Sci., 2018, 41(18), 9321-9334. doi: 10.1002/mma.5263 [4] M. T. Ashordiya, On boundary value problems for systems of linear generalized ordinary differential equations with singularities, Different. Equ., 2006, 42(3), 307-319. doi: 10.1134/S0012266106030013 [5] A. Assanova, An integral-boundary value problem for a partial differential equation of second order, Turk. J. Math., 2019, 43(4), 1967-1978. doi: 10.3906/mat-1903-111 [6] S. R. Baslandze and I. T. Kiguradze, On the unique solvability of a periodic boundary value problem for third-order linear differential equations, Different. Equ., 2006, 42(2), 165-171. doi: 10.1134/S0012266106020029 [7] Y. Cui, W. Ma, et. al, New uniqueness results for boundary value problem of fractional differential equation, Nonlinear. Anal-Model., 2018, 23(1), 31-39. [8] Q. Dang and Q. Dang, Existence results and iterative method for a fully fourth-order nonlinear integral boundary value problem, Numer. Algorithms, 2020, 85(3), 887-907. doi: 10.1007/s11075-019-00842-3 [9] A. Domoshnitsky, R. Hakl and B. Puza, Multi-point boundary value problems for linear functional-differential equations, Georgian. Math. J., 2017, 24(2), 193-206. doi: 10.1515/gmj-2016-0076 [10] D. Dzhumabaev, E. Bakirova and S. Mynbayeva, A method of solving a nonlinear boundary value problem with a parameter for a loaded differential equation, Math. Method. Appl. Sci., 2020, 43(4), 1788-1802. doi: 10.1002/mma.6003 [11] M. Faieghi, S. Kuntanapreeda, H. Delavari, et. al, LMI-based stabilization of a class of fractional-order chaotic systems, Nonlinear. Dynam., 2013, 72(1), 301-309. [12] Z. Ge and C. Ou, Chaos synchronization of fractional order modified duffing systems with parameters excited by a chaotic signal, Chaos. Soliton. Fract., 2008, 35(4), 705-717. doi: 10.1016/j.chaos.2006.05.101 [13] J. R. Graef, L. Kong and B. Yang, Positive solutions for a fractional boundary value problem, Appl. Math. Lett., 2016, 56, 49-55. doi: 10.1016/j.aml.2015.12.006 [14] A. Granas and J. Dugundji, Fixed point theory, Springer, New York, 2003. [15] D. H. Hyers, On the stability of the linear functional equation, P. Natl. Acad. Sci. USA., 1941, 27(4), 222-224. doi: 10.1073/pnas.27.4.222 [16] Z. Jiao, Y. Chen and I. Podlubny, Distributed-order dynamic systems, Springer, New York, 2012. [17] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and applications of fractional differential equations, Elsevier, Amsterdam, 2006. [18] X. Liu and M. Jia, Existence of solutions for the integral boundary value problems of fractional order impulsive differential equations, Math. Method. Appl. Sci., 2016, 39(3), 475-487. doi: 10.1002/mma.3495 [19] N. I. Mahmudov and A. Al-Khateeb, Stability, existence and uniqueness of boundary value problems for a coupled system of fractional differential equations, Mathematics-Basel., 2019, 7(4), 354-366. [20] J. Nan, W. Hu, Y. Su, et. al, Stability and existence of solutions for fractional differential system with p-Laplacian operator on star graphs, Dynam. Syst. Appl., 2022, 31(3), 133-150. [21] R. R. Nigmatullin, The realization of the generalized transfer equation in a medium with fractal geometry, Phys. Status. Solidi. B., 1986, 133(1), 425-430. doi: 10.1002/pssb.2221330150 [22] I. Podlubny, Fractional differential equations, Academic. Press, San Diego, 1999. [23] I. A. Rus, Ulam stabilities of ordinary differential equations in a Banach space, Carpath. J. Math., 2010, 26, 103-107. [24] S. Rezapour, B. Tellab, C. T. Deressa, et. al, HU-type stability and numerical solutions for a nonlinear model of the coupled systems of Navier BVPs via the generalized differential transform method, Fractal. Fract., 2021, 5(4), 166-192. doi: 10.3390/fractalfract5040166 [25] A. Sun, Y. Su and J. Sun, Existence of solutions to a class of fractional differential equations, J. Non. Modeling Anal., 2022, 4(3), 409-442. [26] A. Sun, Y. Su, Q. Yuan, et al, Existence of solutions to fractional differential equations with fractional-order derivative terms, J. Appl. Anal. Comput., 2021, 11(1), 486-520. [27] W. Sun, Y. Su and X. Han, Existence of solutions for a coupled system of Caputo-Hadamard fractional differential equations with $p$-Laplacian operator, J. Appl. Anal. Comput., 2022, 12(5), 1885-1900. [28] W. Sun, Y. Su, A. Sun and Q. Zhu, Existence and simulation of positive solutions for $m$-point fractional differential equations with derivative terms, Open. Math., 2021, 19, 1820-1846. doi: 10.1515/math-2021-0131 [29] Y. Wang and S. Sun, Solvability to infinite-point boundary value problems for singular fractional differential equations on the half-line, J. Appl. Math. Comput., 2018, 57(1), 359-373. [30] H. Wang and R. Rodriguez-Lopez, On the existence of solutions to boundary value problems for interval-valued differential equations under gH-differentiability, Inform. Sciences., 2021, 553, 225-246. doi: 10.1016/j.ins.2020.10.052 [31] Y. Xi, X. Zhang and Y. Su, Uniqueness results of fuzzy fractional differential equations under Krasnoselskii-Krein conditions, Dynam. Syst. Appl., 2021, 30(12), 1792-1801. [32] C. Yuan, X. Wen and D. Jiang, Existence and uniqueness of positive solution for nonlinear singular 2mth-order continuous and discrete Lidstone boundary value problems, Acta. Math. Sci., 2011, 31(1), 281-291. doi: 10.1016/S0252-9602(11)60228-2 [33] X. Zhang, Y. Su and Y. Kong, Positive solutions for boundary value problem of fractional differential equation in Banach spaces, Dynam. Syst. Appl., 2021, 30(9), 1449-1462. [34] F. Zhang, Z. Ma and J. Yan, Functional boundary value problem for first order impulsive differential equations at variable times, Indian. J. Pure. Appl. Math., 2003, 34(5), 733-742. [35] X. Zhou and C. Xu, Well-posedness of a kind of nonlinear coupled system of fractional differential equations, Sci. China. Math., 2016, 59(6), 1209-1220. doi: 10.1007/s11425-015-5113-2 -
-
-
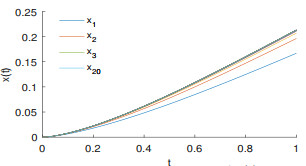
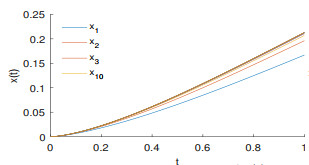
Figure 1.
10-iteration process of
$ x(t) $ -
Figure 2.
20-iteration process of
$ x(t) $ -
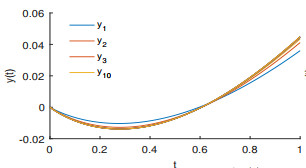
Figure 3.
10-iteration process of
$ y(t) $ -
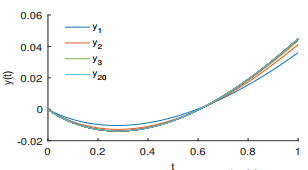
Figure 4.
20-iteration process of
$ y(t) $ -
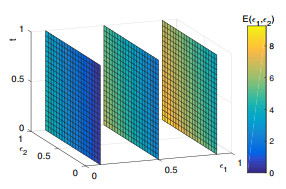
Figure 5.
Approximate value of
$ E(\varepsilon_1, \varepsilon_2) $ -
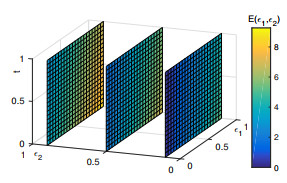
Figure 6.
Approximate value of
$ E(\varepsilon_1, \varepsilon_2) $ -
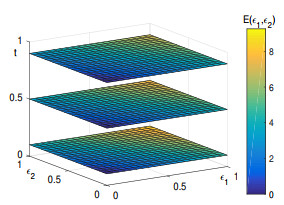
Figure 7.
Approximate value of
$ E(\varepsilon_1, \varepsilon_2) $




 DownLoad:
DownLoad: