| Citation: | Tamer El-Azab, M. Y. Hamada, H. El-Metwally. BIFURCATION AND CHAOS ANALYSIS OF A TWO-DIMENSIONAL DISCRETE-TIME PREDATOR–PREY MODEL[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1910-1930. doi: 10.11948/20220285 |
BIFURCATION AND CHAOS ANALYSIS OF A TWO-DIMENSIONAL DISCRETE-TIME PREDATOR–PREY MODEL
-
Abstract
The dynamical behavior of a discrete predator–prey system with a nonmonotonic functional response is investigated in this work. We study the local asymptotic stability of the positive equilibrium of the system by examining the characteristic equation of the linearized system corresponding to the model. By choosing the growth rate as a bifurcation parameter, the existence of Neimark-Sacker and period-doubling bifurcations at the positive equilibrium is established. Furthermore, the effects of perturbations on the system dynamics are investigated. Finally, examples are presented to illustrate our main results.
-

-
References
[1] H. Agiza, E. ELabbasy, H. EL-Metwally and A. Elsadany, Chaotic dynamics of a discrete prey–predator model with holling type Ⅱ, Nonlinear Analysis: Real World Applications, 2009, 10(1), 116–129. doi: 10.1016/j.nonrwa.2007.08.029 [2] E. S. Allman and J. A. Rhodes, Mathematical models in biology: an introduction, Cambridge University Press, 2004. [3] A. Almutairi, H. El-Metwally, M. Sohaly and I. Elbaz, Lyapunov stability analysis for nonlinear delay systems under random effects and stochastic perturbations with applications in finance and ecology, Advances in Difference Equations, 2021, 2021(1), 1–32. doi: 10.1186/s13662-020-03162-2 [4] A. A. Berryman, The orgins and evolution of predator-prey theory, Ecology, 1992, 73(5), 1530–1535. doi: 10.2307/1940005 [5] J. Carr, Applications of centre manifold theory, Springer Science & Business Media, 2012, 35. [6] J. D. Crawford, Introduction to bifurcation theory, Reviews of Modern Physics, 1991, 63(4), 991. doi: 10.1103/RevModPhys.63.991 [7] Q. Din, Complexity and chaos control in a discrete-time prey-predator model, Communications in Nonlinear Science and Numerical Simulation, 2017, 49, 113–134. doi: 10.1016/j.cnsns.2017.01.025 [8] L. Edelstein-Keshet, Mathematical models in biology, SIAM, 2005. [9] H. El-Metwally, M. Sohaly and I. Elbaz, Mean-square stability of the zero equilibrium of the nonlinear delay differential equation: Nicholson's blowflies application, Nonlinear Dynamics, 2021, 105(2), 1713–1722. doi: 10.1007/s11071-021-06696-6 [10] S. N. Elaydi, Discrete chaos: with applications in science and engineering, Chapman and Hall/CRC, 2007. [11] A. -E. A. Elsadany, H. El-Metwally, E. Elabbasy and H. Agiza, Chaos and bifurcation of a nonlinear discrete prey-predator system, Computational Ecology and Software, 2012, 2(3), 169. [12] Q. Fang and X. Li, Complex dynamics of a discrete predator–prey system with a strong allee effect on the prey and a ratio-dependent functional response, Advances in Difference Equations, 2018, 2018(1), 1–16. doi: 10.1186/s13662-017-1452-3 [13] H. Freedman, A model of predator-prey dynamics as modified by the action of a parasite, Mathematical biosciences, 1990, 99(2), 143–155. doi: 10.1016/0025-5564(90)90001-F [14] S. Gao and L. Chen, The effect of seasonal harvesting on a single-species discrete population model with stage structure and birth pulses, Chaos, Solitons & Fractals, 2005, 24(4), 1013–1023. [15] W. Govaerts, Y. A. Kuznetsov, R. K. Ghaziani and H. Meijer, Cl matcontm: A toolbox for continuation and bifurcation of cycles of maps, Universiteit Gent, Belgium, and Utrecht University, The Netherlands, 2008. [16] J. Guckenheimer and P. Holmes, Nonlinear oscillations, dynamical systems, and bifurcations of vector fields, Springer Science & Business Media, 2013, 42. [17] M. Y. Hamada, T. El-Azab and H. El-Metwally, Allee effect in a ricker type predator-prey model, Journal of Mathematics and Computer Science, 2022, 29(03), 239–251. doi: 10.22436/jmcs.029.03.03 [18] M. Y. Hamada, T. El-Azab and H. El-Metwally, Bifurcation analysis of a two-dimensional discrete-time predator–prey model, Mathematical Methods in the Applied Sciences, 2023, 46(4), 4815–4833. doi: 10.1002/mma.8807 [19] M. Y. Hamada, T. El-Azab and H. El-Metwally, Bifurcations and dynamics of a discrete predator–prey model of ricker type, Journal of Applied Mathematics and Computing, 2022, 69(1), 113–135. [20] H. El-Metwally, AQ. Khan and M. Y. Hamada, Allee effect in a Ricker type discrete-time predator–prey model with Holling type-Ⅱ functional response, Journal of Biological Systems, 2023, 31(2), 1–20. [21] F. C. Hoppensteadt, Mathematical methods of population biology, Cambridge University Press, 1982, 4. [22] G. Iooss, Bifurcation of maps and applications, Elsevier, 1979. [23] F. Kangalgil and S. Kartal, Stability and bifurcation analysis in a host–parasitoid model with hassell growth function, Advances in Difference Equations, 2018, 2018(1), 1–15. doi: 10.1186/s13662-017-1452-3 [24] A. Q. Khan, Bifurcations of a two-dimensional discrete-time predator–prey model, Advances in Difference Equations, 2019, 2019(1), 1–23. doi: 10.1186/s13662-018-1939-6 [25] A. Q. Khan and H. El-Metwally, Global dynamics, boundedness, and semicycle analysis of a difference equation, Discrete Dynamics in Nature and Society, 2021, 2021, 1–10. [26] Y. A. Kuznetsov, Elements of applied bifurcation theory, Springer-Verlag, New York, 2004, 112. [27] Y. A. Kuznetsov and H. G. E. Meijer, Numerical Bifurcation Analysis of Maps: From Theory to Software, Cambridge University Press, 2019. [28] X. Liu and D. Xiao, Complex dynamic behaviors of a discrete-time predator–prey system, Chaos, Solitons & Fractals, 2007, 32(1), 80–94. [29] J. D. Murray, Mathematical biology: I. an introduction. interdisciplinary applied mathematics, Mathematical Biology, Springer, 2002. [30] J. M. Smith and M. Slatkin, The stability of predator-prey systems, Ecology, 1973, 54(2), 384–391. doi: 10.2307/1934346 [31] S. Wiggins and M. Golubitsky, Introduction to applied nonlinear dynamical systems and chaos, Springer, 1990, 2. [32] W. Zhang, Discrete dynamical systems, bifurcations and chaos in economics, elsevier, 2006. [33] J. Zhao and Y. Yan, Stability and bifurcation analysis of a discrete predator–prey system with modified holling–tanner functional response, Advances in Difference Equations, 2018, 2018(1), 1–18. doi: 10.1186/s13662-017-1452-3 -
-
-
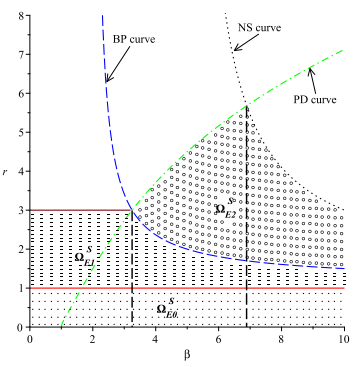
Figure 1.
Stability regions in (
$ \beta, r $ -
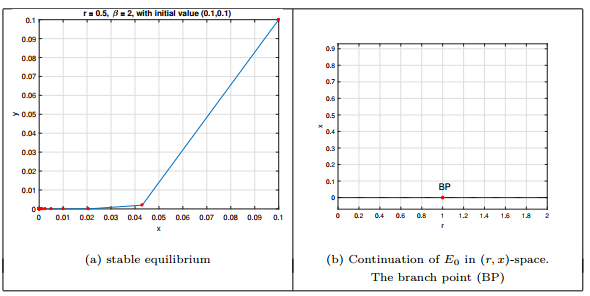
Figure 2.
Phase portrait of equilibrium point
$ E_{0} $ $ E_{1} $ -
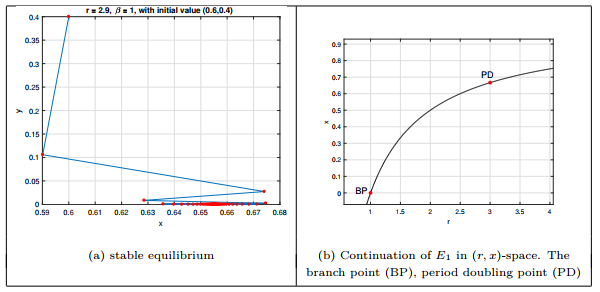
Figure 3.
Phase portraits of equilibrium point
$ E_{1} $ -
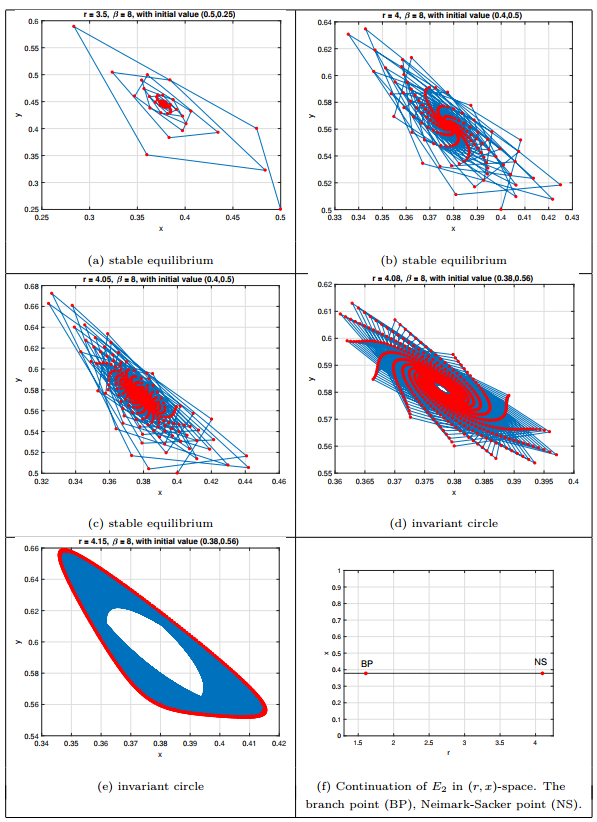
Figure 4.
Phase portraits of equilibrium point
$ E_{2} $ -
Figure 5.
Phase portraits of equilibrium point
$ E_{2} $




 DownLoad:
DownLoad: