| Citation: |
S. Kumbinarasaiah, Mustafa Inc, Hadi Rezazadeh, J. C. Umavathi. A NOVEL TECHNIQUE FOR SOLVING (2+1) DIMENSIONAL SYSTEM OF NONLINEAR COUPLED PARTIAL DIFFERENTIAL EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1890-1909. doi: 10.11948/20220279
|
A NOVEL TECHNIQUE FOR SOLVING (2+1) DIMENSIONAL SYSTEM OF NONLINEAR COUPLED PARTIAL DIFFERENTIAL EQUATION
-
Abstract
We present a highly efficient method to find numerical solutions to the system of PDEs. The method unifies the methods of collocation and Laguerre wavelet series (LWS). The system of (2+1)-dimensional PDEs is reduced to a set of equations having Laguerre wavelet coefficients (LWC). Computational examples are provided to validate the efficiency of the technique and we discussed the comparison between the present method and other methods solution with the exact solution. Computational results indicate that the present method is better than the other methods in the literature.
-
-
References
[1] S. Arbabi, A. Nazari, M. T. Darvishi, A two dimensional Haar wavelets method for solving systems of PDEs, Applied Mathematics and Computation, 2017, 292, 33–46. doi: 10.1016/j.amc.2016.07.032 [2] S. Arbabi, A. Nazari, M.T. Darvishi, A semi-analytical solution of foam drainage equation by Haar wavelets method, Optik, 2016, 127, 5443–5447. doi: 10.1016/j.ijleo.2016.03.032 [3] A. Al-Qudah, Z. Odibat, N. Shawagfeh, A linearization-based computational algorithm of homotopy analysis method for nonlinear reaction–diffusion systems, Math. Comp. Sim., 2022, 194, 505–522. doi: 10.1016/j.matcom.2021.11.027 [4] J. Biazar, M. Eslami, A new homotopy perturbation method for solving systems of partial differential equations, Comput. Math. Appl, 2011, 62, 225–234. [5] J. Biazar, M. Eslami, A new Homotopy perturbation method for solving systems of partial differential equations, Computers and Mathematics with Applications, 2011, 62(1), 225–234. doi: 10.1016/j.camwa.2011.04.070 [6] S. Bekiros, S. Soradi-Zeid, J. Mou, A. Yousefpour, E. Zambrano-Serrano, H. Jahanshahi, Laguerre Wavelet Approach for a Two-Dimensional Time–Space Fractional Schrödinger Equation, Entropy, 2022, 24, 1105. doi: 10.3390/e24081105 [7] M. El-Gamel, W. Adel, M. S. El-Azab, Two Very Accurate and Efficient Methods for Solving Time-Dependent Problems, Applied Mathematics, 2018, 9(11), 1270–1280. doi: 10.4236/am.2018.911083 [8] M. Erfanian, H. Zeidabadi, O. Baghani, Solving an inverse problem for a time-fractional advection-diffusion equation with variable coefficients by rationalized Haar wavelet method, J Comp. Science, 2022, 64, 101869. doi: 10.1016/j.jocs.2022.101869 [9] S. Kumbinarasaiah, A new approach for the numerical solution for nonlinear Klein–Gordon equation, SeMA, 2020, 77, 435–456. doi: 10.1007/s40324-020-00225-y [10] M. Kumar, S. Pandit, A composite numerical scheme for the numerical simulation of coupled Burgers equation, Comput. Phys. Commun., 2014, 185, 809–817. doi: 10.1016/j.cpc.2013.11.012 [11] T. Liu, Porosity reconstruction based on Biot elastic model of porous media by homotopy perturbation method, Chaos, Soliton and Fractals, 2022, 158, 112007. doi: 10.1016/j.chaos.2022.112007 [12] S. Liao, On the homotopy analysis method for nonlinear problems, Applied Mathematics and Computation, 2004, 147, 499–513. doi: 10.1016/S0096-3003(02)00790-7 [13] S. Liao, Comparison between the homotopy analysis method and homotopy perturbation method, Applied Mathematics and Computation, 2005, 169, 1186–1194. doi: 10.1016/j.amc.2004.10.058 [14] T. Liu, A wavelet multiscale-homotopy method for the parameter identification problem of partial differential equations, Computers and Mathematics with Applications, 2016, 17, 1519 -1523. [15] T. Liu, Reconstruction of a permeability field with the wavelet multiscale-homotopy method for a nonlinear convection-diffusion equation, Applied Mathematics and Computation, 2016, 275, 432–437. doi: 10.1016/j.amc.2015.11.095 [16] T. Liu, A multigrid-homotopy method for nonlinear inverse problems, Computers and Mathematics with Applications, 2020, 79, 1706–1717. doi: 10.1016/j.camwa.2019.09.023 [17] T. Liu, A wavelet multiscale method for the inverse problem of a nonlinear convectiondiffusion equation, Journal of Computational and Applied Mathematics, 2018, 330, 165–176. doi: 10.1016/j.cam.2017.08.016 [18] M. Matinfar, M. Saeidy, B. Gharahsuflu, A new homotopy analysis method for finding the exact solution of systems of partial differential equations, Selcuk J. Appl. Math., 2012, 13, 41–56. [19] A. Patra, S. S. Ray, Numerical simulation based on Haar wavelet operational method to solve neutron point kinetics equation involving sinusoidal and pulse reactivity, Ann. Nucl. Energy, 2014, 73, 408–412. doi: 10.1016/j.anucene.2014.07.025 [20] A. Patra, S. S. Ray, Two-dimensional Haar wavelet collocation method for the solution of stationary neutron transport equation in a homogeneous isotropic medium, Ann. Nucl. Energy, 2014, 70, 30–35. doi: 10.1016/j.anucene.2014.01.046 [21] S. S. Ray, A. K. Gupta, Comparative analysis of variational iteration method and Haar wavelet method for the numerical solutions of Burgers-Huxley and Huxley equations, J. Math. Chem., 2014, 52, 1066–1080. doi: 10.1007/s10910-014-0327-z [22] S. S. Ray, A. K. Gupta, On the solution of Burgers-Huxley and Huxley equation using wavelet collocation method, Comput. Model. Eng. Sci., 2013, 91, 409–424. [23] S. C. Shiralashetti, S. Kumbinarasaiah, Hermite wavelets operational matrix of integration for the numerical solution of nonlinear singular initial value problems, Alexandria Engineering Journal, 2018, 57(4), 2591–2600. doi: 10.1016/j.aej.2017.07.014 [24] S. C. Shiralashetti, S. Kumbinarasaiah, Theoretical study on continuous polynomial wavelet bases through wavelet series collocation method for nonlinear Lane-Emden type equations, Applied Mathematics and Computation, 2017, 315, 591–602. doi: 10.1016/j.amc.2017.07.071 [25] S. C. Shiralashetti, S. Kumbinarasaiah, Hermite wavelets method for the numerical solution of linear and nonlinear singular initial and boundary value problems, Computational Methods for Differential Equations, 2019, 7(2), 177–198. [26] S. C. Shiralashetti, S. Kumbinarasaiah, Some Results on Haar Wavelets Matrix through Linear Algebra, Wavelets and Linear Algebra, 2017, 4(2), 49–59. [27] S. C. Shiralashetti, S. Kumbinarasaiah, Cardinal B-spline wavelet based numerical method for the solution of generalized Burgers-Huxley equation, Int. J. Appl. Comput. Math., 2018. Doi: org/10.1007/s40819-018-0505-y. [28] S. C. Shiralashetti, S. Kumbinarasaiah, Laguerre Wavelets Exact Parseval Frame-based Numerical Method for the Solution of System of Differential Equations, Int. J. Appl. Comput. Math., 2020. https://doi.org/10.1007/s40819-020-00848-9. doi: 10.1007/s40819-020-00848-9 [29] Swati, M. Singh, K. Singh, An advancement approach of Haar wavelet method and Bratu-type equations, Appl. Numerical Math., 2021, 170, 74–82. doi: 10.1016/j.apnum.2021.07.014 [30] J. Shahni, R. Singh, Numerical simulation of Emden-Fowler integral equation with Green's function type kernel by Gegenbauer-wavelet, Taylor-wavelet and Laguerre-wavelet collocation methods, Mathematics and Computers in Simulation, 2022, 194, 430–444. doi: 10.1016/j.matcom.2021.12.008 [31] H. Tariq, H. Gunerhan, H. Rezazadeh, W. Adel, A numerical approach for the nonlinear temporal conformable fractional foam drainage equation, Asian-European Journal of Mathematics, 2020. Doi: 10.1142/S1793557121500893. [32] K. Yildirim, A solution method for solving systems of nonlinear PDEs, World Appl. Sci. J., 2012, 1, 1527–1532. -
-
Figures(10) / Tables(6)
Export File
Citation
S. Kumbinarasaiah, Mustafa Inc, Hadi Rezazadeh, J. C. Umavathi. A NOVEL TECHNIQUE FOR SOLVING (2+1) DIMENSIONAL SYSTEM OF NONLINEAR COUPLED PARTIAL DIFFERENTIAL EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1890-1909. doi: 10.11948/20220279
Format
Content
DownLoad:
-
Figure 1.
Graphical representation of ns of
$ u(x, y, 0.01) $ $ u(x, y, 0.01) $ $ u(x, y, 0.01) $ $ M=2 $ $ u(x, y, 0.01) $ $ M=5 $ $ u(x, y, 0.01) $ $ M=2 $ -
Figure 2.
Graphical representation of ns of
$ u(x, y, 0.01) $ $ u(x, y, 0.01) $ $ u(x, y, 0.01) $ $ M=2 $ $ u(x, y, 0.01) $ $ M=5 $ $ u(x, y, 0.01) $ $ M=2 $ -
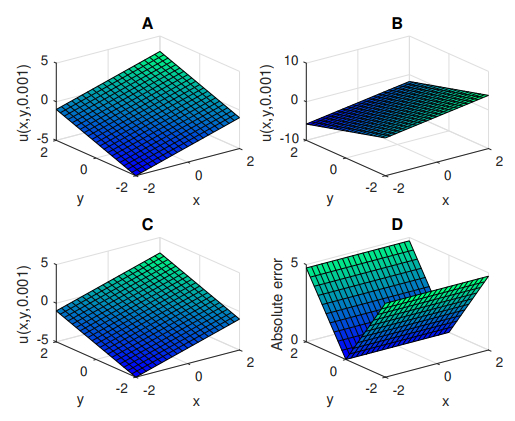
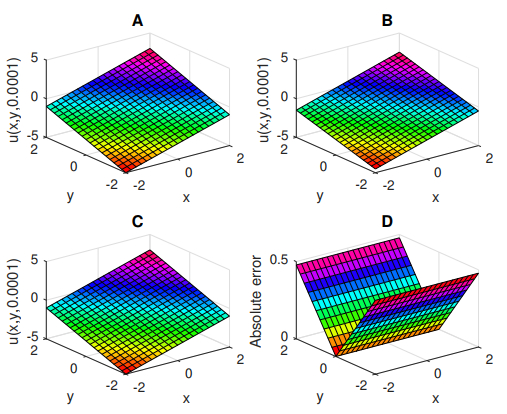
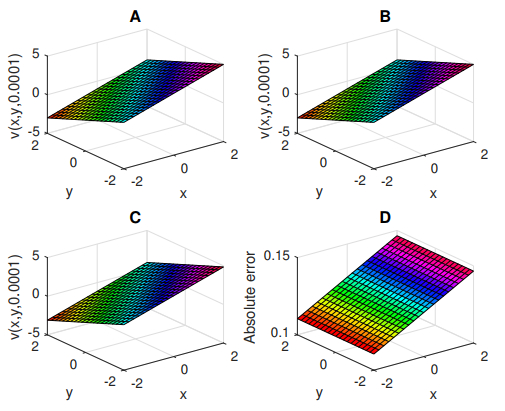
Figure 3.
Graphical representation of ns of
$ u(x, y, 0.0001) $ $ u(x, y, 0.0001) $ $ u(x, y, 0.0001) $ $ M=2 $ $ u(x, y, 0.0001) $ $ M=5 $ $ u(x, y, 0.0001) $ $ M=2 $ -
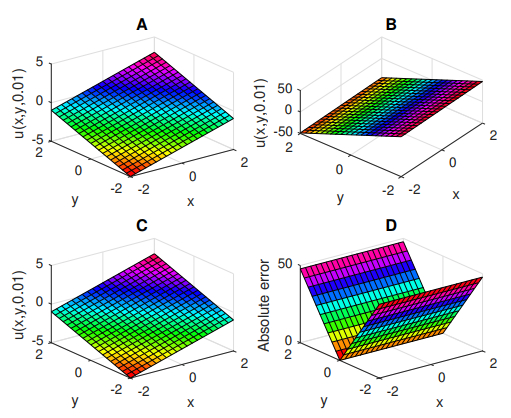
Figure 4.
Graphical representation of ns of
$ v(x, y, 0.01) $ $ v(x, y, 0.01) $ $ v(x, y, 0.01) $ $ M=2 $ $ v(x, y, 0.01) $ $ M=5 $ $ v(x, y, 0.01) $ $ M=2 $ -
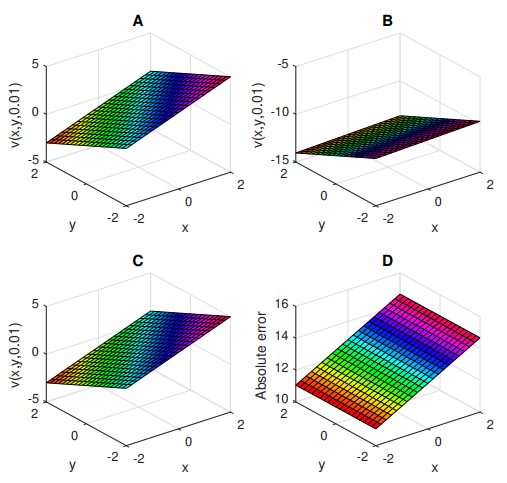
Figure 5.
Graphical representation of ns of
$ v(x, y, 0.001) $ $ v(x, y, 0.001) $ $ v(x, y, 0.001) $ $ M=2 $ $ v(x, y, 0.001) $ $ M=5 $ $ v(x, y, 0.001) $ $ M=2 $ -
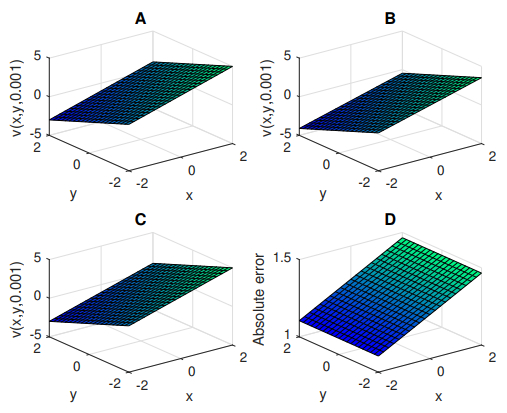
Figure 6.
Graphical representation of ns of
$ v(x, y, 0.0001) $ $ v(x, y, 0.0001) $ $ v(x, y, 0.0001) $ $ M=2 $ $ v(x, y, 0.0001) $ $ M=5 $ $ v(x, y, 0.0001) $ $ M=2 $ -
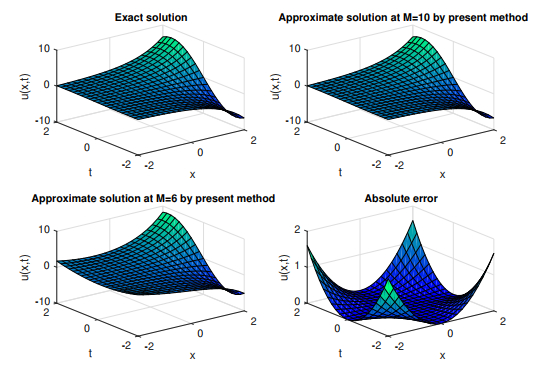
Figure 7.
Graphical representation of es
$ u(x, t) $ $ k=1 $ $ M=10, 6 $ -
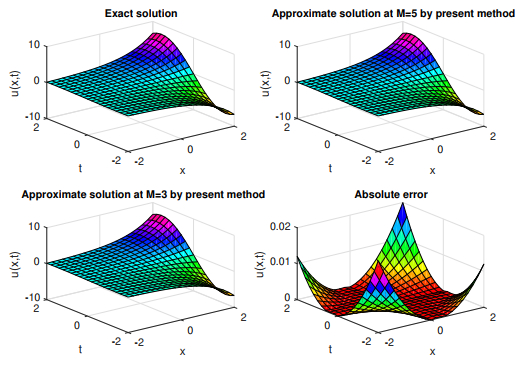
Figure 8.
Graphical representation of es
$ u(x, t) $ $ k=2 $ $ M=5, 3 $ -
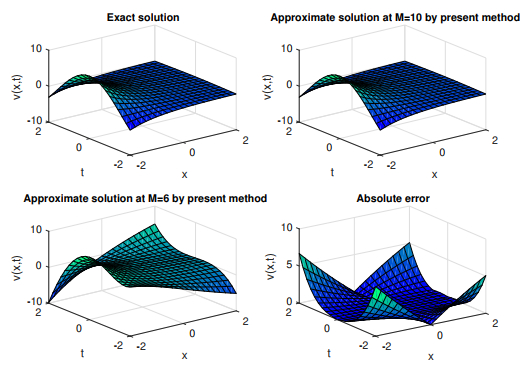
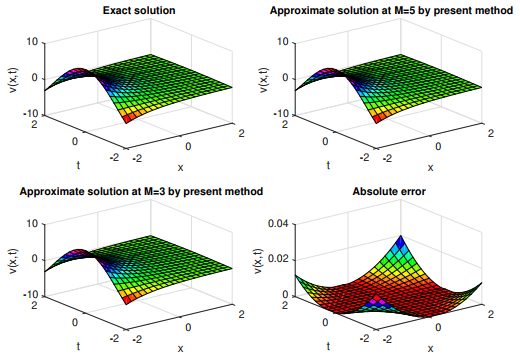
Figure 9.
Graphical representation of es
$ v(x, t) $ $ k=1 $ $ M=10, 6 $ -
Figure 1.
Graphical representation of es
$ v(x, t) $ $ k=2 $ $ M=5, 3 $