| Citation: | Jicheng Yu, Yuqiang Feng. LIE SYMMETRY, EXACT SOLUTIONS AND CONSERVATION LAWS OF SOME FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1872-1889. doi: 10.11948/20220268 |
LIE SYMMETRY, EXACT SOLUTIONS AND CONSERVATION LAWS OF SOME FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS
-
Abstract
In this paper, Lie symmetry analysis method is applied to space-time fractional reaction-diffusion equations and diffusion-convection Boussinesq equations. The Lie symmetries for the governing equations are obtained and used to get group generators for reducing the space-time fractional partial differential equations(FPDEs) with Riemann-Liouville fractional derivative to space-time fractional ordinary differential equations(FODEs) with Erdélyi-Kober fractional derivative. Then the Laplace transformation and the power series methods are applied to derive explicit solutions for the reduced equations. Moreover, the conservation theorems and the generalization of the Noether operators are developed to acquire the conservation laws for the equations. Some figures for the obtained explicit solutions are also presented.
-

-
References
[1] J. Boussinesq, Recherches théorique sur l'écoulement des nappes d'eau infiltrées dans le sol et sur le débit des sources, J. Math. Pures Appl., 1904, 10, 5–78. [2] D. Baleanu, M. Inc, A. Yusuf, et al., Space-time fractional Rosenou-Haynam equation: Lie symmetry analysis, explicit solutions and conservation laws, Adv. Differ. Equ. Ny., 2018, 1, 1–14. [3] E. H. El Kinani and A. Ouhadan, Lie symmetry analysis of some time fractional partial differential equations, Int. J. Mod. Phys. Conf. Ser., 2015, 38, 1560075. doi: 10.1142/S2010194515600757 [4] R. K. Gazizov, A. A. Kasatkin and S. Y. Lukashchuk, Continuous transformation groups of fractional differential equations, Vestnik USATU, 2007, 9, 125–135. [5] R. K. Gazizov, A. A. Kasatkin and S. Y. Lukashchuk, Symmetry properties of fractional diffusion equations, Phys. Scr., 2009, T136, 014016. doi: 10.1088/0031-8949/2009/T136/014016 [6] V. A. Galaktionov and S. R. Svirshchevskii, Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics, Chapman and Hall/CRC, London, 2007. [7] R. Hilfer, Applications of fractional calculus in physics, Singapore: World Scientific, Singapore, 2000. [8] M. S. Hashemi and D. Baleanu, Lie symmetry analysis of fractional differential equations, CRC Press, Boca Raton, FL, 2020. [9] Q. Huang and S. Shen, Lie symmetries and group classification of a class of time fractional evolution systems, J. Math. Phys., 2015, 56, 123504. doi: 10.1063/1.4937755 [10] M. Inc, A. Yusuf, A. I. Aliyu, et al., Lie symmetry analysis, explicit solutions and conservation laws for the space time fractional nonlinear evolution equations, Phys. A, 2018, 496, 371–383. doi: 10.1016/j.physa.2017.12.119 [11] N. H. Ibragimov, Nonlinear self-adjointness and conservation laws, J. Phys. A-Math. Theor., 2011, 44, 432002. doi: 10.1088/1751-8113/44/43/432002 [12] N. H. Ibragimov, A new conservation theorem, J. Math. Anal. Appl., 2007, 333, 311–328. doi: 10.1016/j.jmaa.2006.10.078 [13] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and applications of fractional differential equations, Elsevier, New York, 2006. [14] A. M. Nass, Symmetry analysis of space-time fractional Poisson equation with a delay, Quaest. Math., 2019, 42, 1221–1235. doi: 10.2989/16073606.2018.1513095 [15] I. Podlubny, Fractional differential equations, Academic Press, San Diego, 1999. [16] S. G. Samko, A. A. Kilbas and O. I. Marichev, Fractional integrals and derivatives: theory and applications, Gordon and Breach Science Publishers, Yverdon, 1993. [17] K. Singla and R. K. Gupta, Comment on "Lie symmetries and group classification of a class of time fractional evolution systems"[J. Math. Phys. 56, 123504 (2015)], J. Math. Phys., 2017, 58, 054101. [18] K. Singla and R. K. Gupta, On invariant analysis of some time fractional nonlinear systems of partial differential equations. I, J. Math. Phys., 2016, 57, 101504. doi: 10.1063/1.4964937 [19] K. Singla and R. K. Gupta, On invariant analysis of space-time fractional nonlinear systems of partial differential equations. Ⅱ, J. Math. Phys., 2017, 58, 051503. doi: 10.1063/1.4982804 [20] R. Sahadevan and P. Prakash, On Lie symmetry analysis and invariant subspace methods of coupled time fractional partial differential equations, Chaos, Solitons and Fractals, 2017, 104, 107–120. doi: 10.1016/j.chaos.2017.07.019 [21] M. Yourdkhany and M. Nadjafikhah, Symmetries, similarity invariant solution, conservation laws and exact solutions of the time-fractional Harmonic Oscillator equation, J. Geom. Phys., 2020, 153, 103661. doi: 10.1016/j.geomphys.2020.103661 [22] J. Yu, Lie symmetry analysis of time fractional Burgers equation, Korteweg-de Vries equation and generalized reaction-diffusion equation with delays, Int. J. Geom. Methods M., 2022, 19, 2250219. [23] J. Yu and Y. Feng, Lie symmetry analysis and exact solutions of space-time fractional cubic Schrödinger equation, Int. J. Geom. Methods M., 2022, 19, 2250077. [24] Z. Zhang, Symmetry determination and nonlinearization of a nonlinear time-fractional partial differential equation, Proc. R. Soc. A, 2020, 476, 20190564. doi: 10.1098/rspa.2019.0564 [25] Z. Zhang and G. Li, Lie symmetry analysis and exact solutions of the time-fractional biological population model, Phys. A, 2020, 540, 123134. doi: 10.1016/j.physa.2019.123134 -
-
-
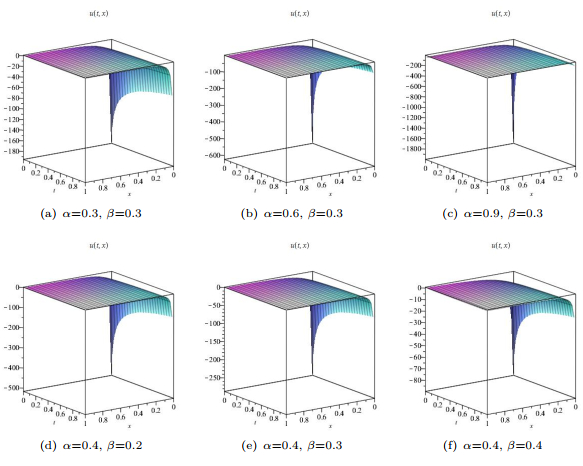
Figure 1.
Graphs of solutions (3.27) with
$ k_1=\frac{\Gamma(1-\alpha) }{\Gamma(1-2\alpha) } $ $ k_2=1 $ -
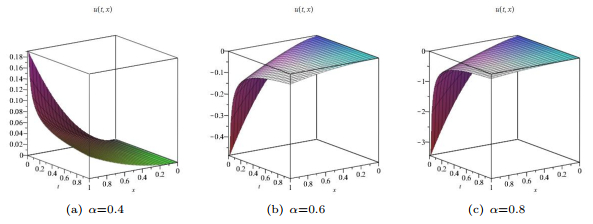
Figure 2.
Graphs of solutions (3.28) with
$ k_1=\frac{\Gamma(1-\alpha) }{\Gamma(1-2\alpha) } $ $ k_2=k_3=1 $ -
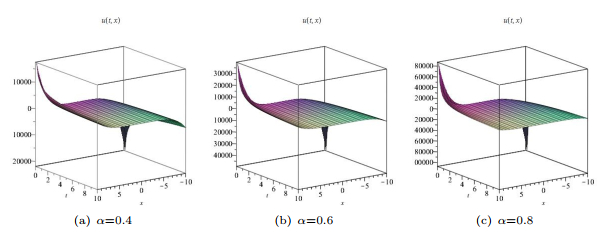
Figure 3.
Graphs of solutions (4.15) with
$ k=l=1 $ -
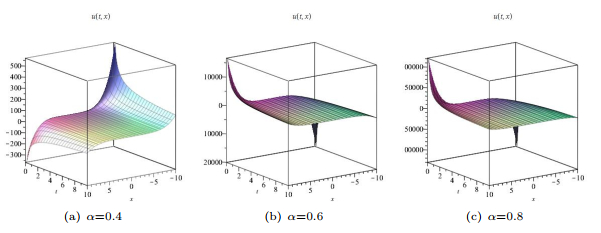
Figure 4.
Numerical simulation of the power series solutions (4.31) with
$ k=l=a_0=a_1=1 $ -
Figure 5.
Numerical simulation of the power series solutions (4.31) with
$ k=l=1 $ $ a_0=a_1=0.1 $





 DownLoad:
DownLoad: