| Citation: | Amjid Ali, Teruya Minamoto. A NEW NUMERICAL TECHNIQUE FOR SOLVING ψ-FRACTIONAL RICCATI DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 1027-1043. doi: 10.11948/20220318 |
A NEW NUMERICAL TECHNIQUE FOR SOLVING ψ-FRACTIONAL RICCATI DIFFERENTIAL EQUATIONS
-
Abstract
This paper proposes a new numerical technique for solving a specific class of fractional differential equations, which includes the ψ-Caputo fractional derivative. The class under consideration is nonlinear ψ-fractional Riccati differential equations (ψ-FRDEs). Our approach relies on the ψ-Haar wavelet (ψ-HW) operational matrix, which is a novel type of operational matrix of fractional integration. We derive an explicit formula for the ψ-fractional integral of the HW. This operational matrix has been used successfully to solve nonlinear ψ-FRDEs.The Quasi-linearization technique is employed to linearize the non-linear ψ-FRDEs. This technique reduces the problem to an algebraic equation that can be easily solved. The technique is a useful and straightforward mathematical tool for solving nonlinear ψ-FRDEs. The computational complexity of the operational matrix technique is minimal. The error analysis of the proposed method is thoroughly investigated. To justify the method's accuracy and efficiency, numerical results are given.
-

-
References
[1] L. Akinyemi and O. S. Iyiola, A reliable technique to study nonlinear time-fractional coupled Korteweg-De vries equations, Advances in Difference equations, 2020, 2020(1), 1-27. doi: 10.1186/s13662-019-2438-0 [2] L. Akinyemi, O. S. Iyiola and U. Akpan, Iterative methods for solving fourth-and sixth-order time-fractional Cahn-Hillard equation, Mathematical Methods in the Applied Sciences, 2020, 43(7), 4050-4074. [3] L. Akinyemi, M. Şenol and S. N. Huseen, Modified homotopy methods for generalized fractional perturbed Zakharov-Kuznetsov equation in dusty plasma, Advances in Difference Equations, 2021, 2021(1), 1-27. doi: 10.1186/s13662-020-03162-2 [4] A. Alharbi and M. Almatrafi, Riccati-Bernoulli sub-ode approach on the partial differential equations and applications, International Journal of Mathematics and Computer Science, 2020, 15(1), 367-388. [5] R. Almeida, A caputo fractional derivative of a function with respect to another function, Communications in Nonlinear Science and Numerical Simulation, 2017, 44, 460-481. doi: 10.1016/j.cnsns.2016.09.006 [6] R. Almeida, Fractional differential equations with mixed boundary conditions, Bulletin of the Malaysian Mathematical Sciences Society, 2019, 42(4), 1687-1697. doi: 10.1007/s40840-017-0569-6 [7] R. Almeida, M. Jleli and B. Samet, A numerical study of fractional relaxation-oscillation equations involving ψ-caputo fractional derivative, Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas, 2019, 113(3), 1873-1891. doi: 10.1007/s13398-018-0590-0 [8] R. Almeida, A. B. Malinowska and M. T. T. Monteiro, Fractional differential equations with a caputo derivative with respect to a kernel function and their applications, Mathematical Methods in the Applied Sciences, 2018, 41(1), 336-352. doi: 10.1002/mma.4617 [9] R. Almeida, A. B. Malinowska and T. Odzijewicz, An extension of the fractional Gronwall inequality, in Conference on Non-Integer Order Calculus and Its Applications, Springer, 2018, 20-28. [10] R. Amin, B. Alshahrani, M. Mahmoud et al., Haar wavelet method for solution of distributed order time-fractional differential equations, Alexandria Engineering Journal, 2021, 60(3), 3295-3303. doi: 10.1016/j.aej.2021.01.039 [11] A. Ansari, A. Refahi Sheikhani and H. Saberi Najafi, Solution to system of partial fractional differential equations using the fractional exponential operators, Mathematical Methods in the Applied Sciences, 2012, 35(1), 119-123. doi: 10.1002/mma.1545 [12] E. Babolian and A. Shahsavaran, Numerical solution of nonlinear Fredholm integral equations of the second kind using Haar wavelets, Journal of Computational and Applied Mathematics, 2009, 225(1), 87-95. doi: 10.1016/j.cam.2008.07.003 [13] R. Bagley and P. Torvik, On the existence of the order domain and the solution of distributed order equations-part Ⅰ, International Journal of Applied Mathematics, 2000, 2(7), 865-882. [14] R. Bagley and P. Torvik, On the existence of the order domain and the solution of distributed order equations-part Ⅱ, International Journal of Applied Mathematics, 2000, 2(8), 965-988. [15] M. Caputo, Mean fractional-order-derivatives differential equations and filters, Annali dell'Universita di Ferrara, 1995, 41(1), 73-84. doi: 10.1007/BF02826009 [16] Y. Chen, M. Yi and C. Yu, Error analysis for numerical solution of fractional differential equation by Haar wavelets method, Journal of Computational Science, 2012, 3(5), 367-373. doi: 10.1016/j.jocs.2012.04.008 [17] R. Conte and M. Musette, Link between solitary waves and projective Riccati equations, Journal of Physics A: Mathematical and General, 1992, 25(21), 5609. doi: 10.1088/0305-4470/25/21/019 [18] M. Gerber, B. Hasselblatt and D. Keesing, The Riccati equation: pinching of forcing and solutions, Experimental Mathematics, 2003, 12(2), 129-134. doi: 10.1080/10586458.2003.10504488 [19] M. Gohar, Approximate solution to fractional Riccati differential equations, Fractals, 2019, 27(08), 1950128. doi: 10.1142/S0218348X19501287 [20] O. Iyiola, B. Oduro and L. Akinyemi, Analysis and solutions of generalized Chagas vectors re-infestation model of fractional order type, Chaos, Solitons & Fractals, 2021, 145, 110797. [21] N. Jibenja, B. Yuttanan and M. Razzaghi, An efficient method for numerical solutions of distributed-order fractional differential equations, Journal of Computational and Nonlinear Dynamics, 2018, 13(11). [22] N. A. Khan, A. Ara and M. Jamil, An efficient approach for solving the Riccati equation with fractional orders, Computers & Mathematics with Applications, 2011, 61(9), 2683-2689. [23] M. M. Khashan, R. Amin and M. I. Syam, A new algorithm for fractional Riccati type differential equations by using Haar wavelet, Mathematics, 2019, 7(6), 545. doi: 10.3390/math7060545 [24] A. Kilbas, Theory and applications of fractional differential equations. [25] V. V. Kulish and J. L. Lage, Application of fractional calculus to fluid mechanics, J. Fluids Eng., 2002, 124(3), 803-806. doi: 10.1115/1.1478062 [26] A. Lim, Y. Liu, K. Teo and J. Moore, Linear-quadratic optimal control with integral quadratic constraints, Optimal control applications and methods, 1999, 20(2), 79-92. doi: 10.1002/(SICI)1099-1514(199903/04)20:2<79::AID-OCA647>3.0.CO;2-3 [27] K. Maleknejad, J. Rashidinia and T. Eftekhari, Numerical solutions of distributed order fractional differential equations in the time domain using the Müntz-Legendre wavelets approach, Numerical Methods for Partial Differential Equations, 2021, 37(1), 707-731. doi: 10.1002/num.22548 [28] I. Owusu-Mensah, L. Akinyemi, B. Oduro and O. S. Iyiola, A fractional order approach to modeling and simulations of the novel Covid-19, Advances in Difference Equations, 2020, 2020(1), 1-21. doi: 10.1186/s13662-019-2438-0 [29] Y. Öztürk, A. Anapalı, M. Gülsu and M. Sezer, A collocation method for solving fractional Riccati differential equation, Journal of Applied Mathematics, 2013, 2013. [30] M. Pourbabaee and A. Saadatmandi, A novel Legendre operational matrix for distributed order fractional differential equations, Applied Mathematics and Computation, 2019, 361, 215-231. doi: 10.1016/j.amc.2019.05.030 [31] J. Rashidinia, T. Eftekhari and K. Maleknejad, A novel operational vector for solving the general form of distributed order fractional differential equations in the time domain based on the second kind Chebyshev wavelets, Numerical Algorithms, 2021, 88(4), 1617-1639. doi: 10.1007/s11075-021-01088-8 [32] D. Sierociuk, A. Dzieliński, G. Sarwas et al., Modelling heat transfer in heterogeneous media using fractional calculus, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2013, 371(1990), 20120146. [33] I. Sokolov, A. Chechkin and J. Klafter, Distributed-order fractional kinetics, arXiv preprint cond-mat/0401146, 2004. [34] B. Yuttanan, M. Razzaghi and T. N. Vo, Fractional-order generalized Legendre wavelets and their applications to fractional Riccati differential equations, International Journal of Nonlinear Sciences and Numerical Simulation, 2021. -
-
-
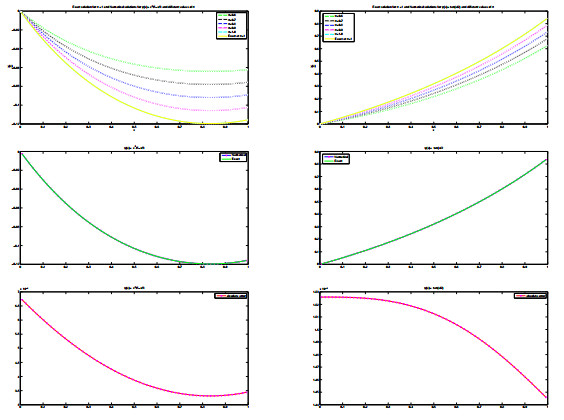
Figure 1.
Actual and approximate results of the problem (5.1) for
$ J=6 $ $ \gamma $ -
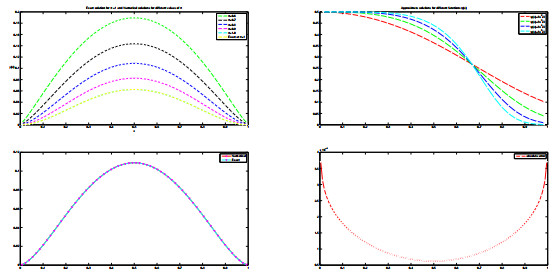
Figure 2.
Actual and Approximate results of problem (5.7) for different fractional orders,
$ \gamma $ $ \max $ -
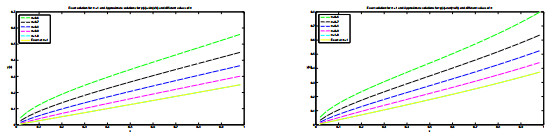
Figure 3.
Approx results for various
$ \gamma $ $ {\psi}(x) $ -
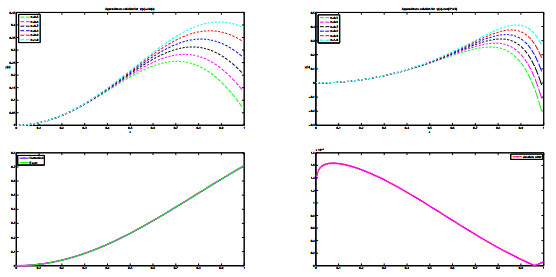
Figure 4.
Approximate results for
$ \gamma=1, \; J=6 $ $ {\psi}(\varkappa) $




 DownLoad:
DownLoad: