| Citation: |
Qimei Zhou, Yuming Chen, Shangming Chen, Fengde Chen. DYNAMIC ANALYSIS OF A DISCRETE AMENSALISM MODEL WITH ALLEE EFFECT[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2416-2432. doi: 10.11948/20220332
|
DYNAMIC ANALYSIS OF A DISCRETE AMENSALISM MODEL WITH ALLEE EFFECT
-
Abstract
This paper concerns with a discretization of a continuous-time amensalism model with Allee effect on the first species. Compared with the continuous analog, the discrete system has different and quite rich dynamical behavior. First, we obtain the existence of fixed points and their local stabilities. Then we confirm the occurrence of fold bifurcation and period doubling bifurcation by using the center manifold theorem and bifurcation theory. Followed is a hybrid control strategy to control the period-doubling bifurcation and stabilize unstable periodic orbits embedded in the complex attractor. Numerical simulations indicate that Allee effect is beneficial to the stability of the first species to a certain extent. Moreover, when the first species is affected by Allee effect, solutions can quickly approach the corresponding fixed point.
-
-
References
[1] W. C. Allee, Animal Aggregations: A Study in General Sociology, University of Chicago Press, Chicago, 1931. [2] Z. AlSharawi, S. Pal, N. Pal, et al., A discrete-time model with non-monotonic functional response and strong Allee effect in prey, J. Difference Equ. Appl., 2020, 26(3), 404–431. doi: 10.1080/10236198.2020.1739276 [3] C. Celik and O. Duman, Allee effect in a discrete-time predator–prey system, Chaos Solitons Fractals, 2009, 40(4), 1956–1962. doi: 10.1016/j.chaos.2007.09.077 [4] P. Chakraborty, U. Ghosh and S. Sarkar, Stability and bifurcation analysis of a discrete prey–predator model with square-root functional response and optimal harvesting, J. Biol. Systems, 2020, 28(01), 91–110. doi: 10.1142/S0218339020500047 [5] B. Chen, Dynamic behaviors of a non-selective harvesting Lotka-Volterra amensalism model incorporating partial closure for the populations, Adv. Difference Equ., 2018, 2018, Article ID: 111. doi: 10.1186/s13662-018-1555-5 [6] L. Cheng and H. Cao, Bifurcation analysis of a discrete-time ratio-dependent predator–prey model with Allee effect, Commun. Nonlinear Sci. Numer. Simul., 2016, 38, 288–302. doi: 10.1016/j.cnsns.2016.02.038 [7] Q. Din, Controlling chaos in a discrete-time prey-predator model with Allee effects, Int. J. Dyn. Control, 2018, 6(2), 858–872. doi: 10.1007/s40435-017-0347-1 [8] Z. Eskandari, J. Alidousti, Z. Avazzadeh, et al., Dynamics and bifurcations of a discrete-time prey-predator model with Allee effect on the prey population, Ecol. Complex., 2021, 48, 100962. doi: 10.1016/j.ecocom.2021.100962 [9] S. Elaydi, An Introduction to Difference Equation, Springer-Verlag, 1996. [10] X. Guan and F. Chen, Dynamical analysis of a two species amensalism model with Beddington-DeAngelis functional response and Allee effect on the second species, Nonlinear Anal. Real World Appl., 2019, 48, 71–93. doi: 10.1016/j.nonrwa.2019.01.002 [11] J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer Science & Business Media, 2013. [12] Z. Guo, H. Huo, Q. Ren, et al., Bifurcation of a modified Leslie-Gower system with discrete and distributed delays, J. Nonlinear Model. Anal., 2019, 1(1), 73–91. [13] S. Işık, A study of stability and bifurcation analysis in discrete-time predator-prey system involving the Allee effect, Int. J. Biomath., 2019, 12(01), 1950011. doi: 10.1142/S1793524519500116 [14] C. Lei, Dynamic behaviors of a stage structure amensalism system with a cover for the first species, Adv. Difference Equ., 2018, 2018, Article ID: 272. doi: 10.1186/s13662-018-1729-1 [15] Q. Lin and X. Zhou, On the existence of positive periodic solution of a amensalism model with Holling II functional response, Commun. Math. Biol. Neurosci., 2017, 2017, Article ID: 3. [16] X. Liu and D. Xiao, Complex dynamic behaviors of a discrete-time predator-prey system, Chaos Solitons Fractals, 2007, 32, 80–94. doi: 10.1016/j.chaos.2005.10.081 [17] D. Luo and Q. Wang, Global dynamics of a Holling-II amensalism system with nonlinear growth rate and Allee effect on the first species, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2021, 31(03), 2150050. doi: 10.1142/S0218127421500504 [18] X. Luo, G. Chen, B. Wang, et al., Hybrid control of period-doubling bifurcation and chaos in discrete nonlinear dynamical systems, Chaos Solitons Fractals, 2003, 18, 775–783. doi: 10.1016/S0960-0779(03)00028-6 [19] R. Ma, Y. Bai and F. Wang, Dynamical behavior analysis of a two-dimensional discrete predator-prey model with prey refuge and fear factor, J. Appl. Anal. Comput., 2020, 10(4), 1683–1697. [20] D. L. Ogada, M. E. Gadd, R. S. Ostfeld, et al., Impacts of large herbivorous mammals on bird diversity and abundance in an African savanna, Oecologia, 2018, 156, 387–397. [21] S. S. Rana, Bifurcations and chaos control in a discrete-time predator-prey system of Leslie type, J. Appl. Anal. Comput., 2019, 9(1), 31–44. [22] C. Robinson, Dynamical Systems: Stability, Symbolic Dynamics and Chaos, CRC Press, 1998. [23] Q. Su and F. Chen, The influence of partial closure for the populations to a non-selective harvesting Lotka-Volterra discrete amensalism model, Adv. Difference Equ., 2019, 2019, Article ID: 281. doi: 10.1186/s13662-019-2209-y [24] G. Sun, Qualitative analysis on two populations amensalism model, Jiamusi University (Natural Science Edition), 2003, 21(3), 283–286. doi: 10.3969/j.issn.1008-1402.2003.03.014 [25] Z. Wei, Y. Xia and T. Zhang, Stability and bifurcation analysis of an amensalism model with weak Allee effect, Qual. Theory Dyn. Syst., 2020, 19(1), 1–15. doi: 10.1007/s12346-019-00337-5 [26] R. Wu, L. Zhao and Q. Lin, Stability analysis of a two species amensalism model with Holling II functional response and a cover for the first species, J. Nonlinear Funct. Anal., 2016, 2016, Article ID: 46. [27] X. Xi, J. N. Griffin and S. Sun, Grasshoppers amensalistically suppress caterpillar performance and enhance plant biomass in an alpine meadow, Oikos, 2013, 122(7), 1049–1057. doi: 10.1111/j.1600-0706.2012.00126.x [28] X. Xie, F. Chen and M. He, Dynamic behaviors of two species amensalism model with a cover for the first species, J. Math. Comput. Sci., 2016, 16, 395–401. doi: 10.22436/jmcs.016.03.09 [29] J. Yan, C. Li, X. Chen, et al., Dynamic complexities in 2-dimensional discrete-time predator-prey systems with Allee effect in the prey, Discrete Dyn. Nat. Soc., 2016, 2016, Article ID: 4275372. [30] L. Zhang and L. Zou, Bifurcations and control in a discrete predator-prey model with strong Allee effect, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2018, 28(05), 1850062. doi: 10.1142/S0218127418500621 [31] M. Zhao and Y. Du, Stability and bifurcation analysis of an amensalism system with Allee effect, Adv. Difference Equ., 2020, 2020, Article ID: 341. doi: 10.1186/s13662-020-02804-9 [32] M. Zhao, C. Li and J. Wang, Complex dynamic behaviors of a discrete-time predator-prey system, J. Appl. Anal. Comput., 2017, 7(2), 478–500. [33] Q. Zhou, F. Chen and S. Lin, Complex dynamics analysis of a discrete amensalism system with a cover for the first species, Axioms, 2022, 11(8), 365. doi: 10.3390/axioms11080365 -
-
Figures(8)
Export File
Citation
Qimei Zhou, Yuming Chen, Shangming Chen, Fengde Chen. DYNAMIC ANALYSIS OF A DISCRETE AMENSALISM MODEL WITH ALLEE EFFECT[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2416-2432. doi: 10.11948/20220332
Format
Content
DownLoad:
-
Figure 1.
When
$ (\alpha, m, \beta)=(2.2, 0, 0.8) $ $ E^*(1.4, 1) $ $ (x_0, y_0)=(0.5, 0.6) $ -
Figure 2.
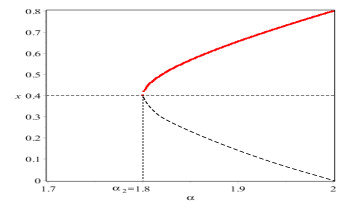
The fold bifurcation diagram of system (1.5) at the fixed point
$ E_3^*(x_3^*, 1) $ $ \alpha=\alpha_2=1.8 $ $ m=0.4, \beta=0.8 $ $ \gamma=0.5 $ -
Figure 3.
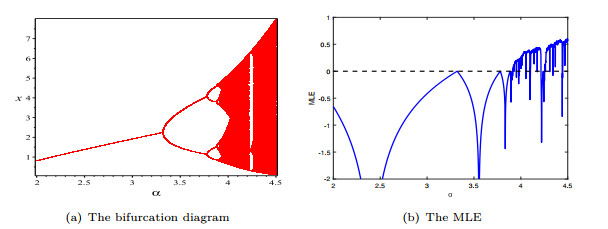
The period-doubling bifurcation diagram of (1.5) at
$ E_2^*(2.25, 1) $ $ \alpha $ $ (\beta, m, \gamma)=(0.8, 0.5, 0.4) $ $ \alpha=\alpha^{**}\approx 3.32 $ -
Figure 4.
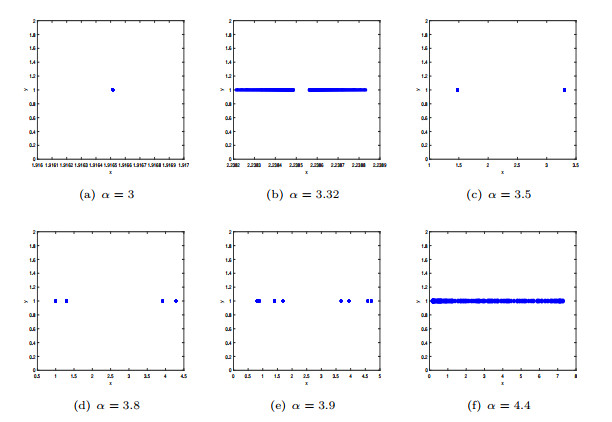
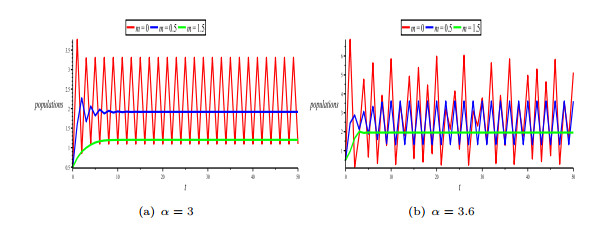
Phase portraits for various values of
$ \alpha $ -
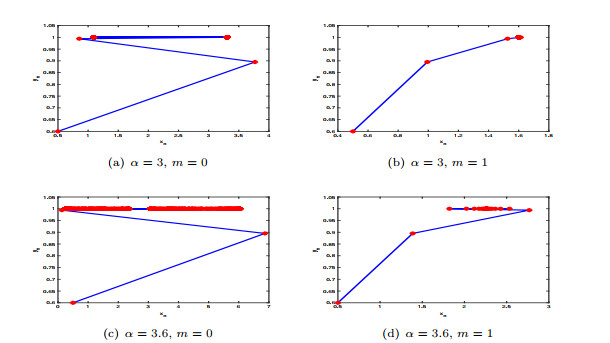
Figure 5.
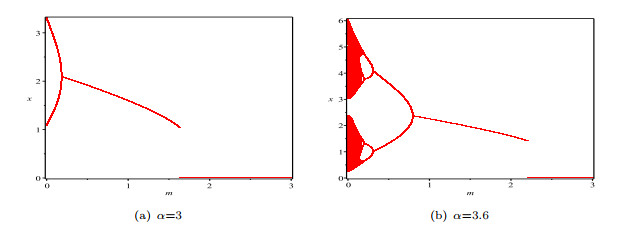
The bifurcation diagram with
$ m $ -
Figure 6.
Time series of solutions of system (1.5) with different values of
$ m $ -
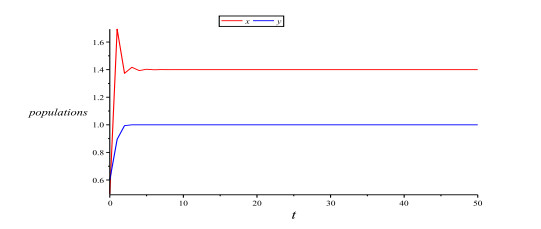
Figure 7.
Trajectories of the densities of the first and second species with
$ (x_0, y_0) = (0.5, 0.6) $ -
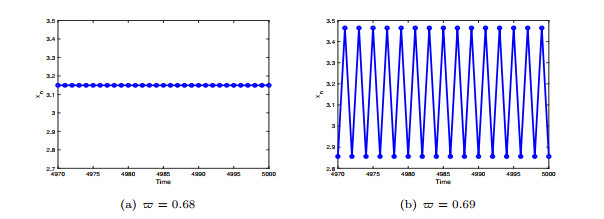
Figure 8.
Time series of the first species for the controlled system (5.1) with different
$ \varpi $ $ \alpha=4.2 $ $ \beta=0.8 $ $ m=0.5 $ $ \gamma=0.4 $ $ (x_0, y_0)=(0.5, 0.6) $