| Citation: |
Ashish, Jinde Cao, Muhammad Aslam Noor. STABILIZATION OF FIXED POINTS IN CHAOTIC MAPS USING NOOR ORBIT WITH APPLICATIONS IN CARDIAC ARRHYTHMIA[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2452-2470. doi: 10.11948/20220350
|
STABILIZATION OF FIXED POINTS IN CHAOTIC MAPS USING NOOR ORBIT WITH APPLICATIONS IN CARDIAC ARRHYTHMIA
-
Abstract
Controlling chaos through stability in fixed and periodic states is used in various engineering problems such as heat convection, reduction control, spine-wave instability, traffic control models, cardiac arrhythmia, chemical chaos, etc. Traditionally, this process is done in the coordination of chaos and stability in fixed and periodic points by using fixed point iterative procedures. Therefore, this article deals with a novel alliance between stabilization in one-dimensional discrete maps and Noor fixed point iterative procedure. The procedure contains $\alpha$, $\beta$, $\gamma$ and $r$, as its four new control parameters due to which the stability rate increases more rapidly than the other existing procedures. The stability theorems and a few time varying examples for fixed and periodic points are studied using Noor control system. Further, the Lyapunov exponent property is also described and the maximum Lyapunov value is determined to examine the stability in fixed and periodic points. Moreover, an improved control-based cardiac arrhythmia model is discussed in the Noor control system. Surprisingly, it is noted that the added new parameters $\alpha$, $\beta$, and $\gamma$ may increase the stability in chaotic arrhythmia rapidly.
-
Keywords:
- Chaos /
- stability /
- lterative procedure /
- difference maps /
- Lyapunov exponent
-
-
References
[1] Ashish, M. Rani and R. Chugh, Julia sets and Mandelbrot sets in Noor orbit, Appl. Math. Comput., 2014, 228, 615–631. [2] Ashish, J. Cao and R. Chugh, Chaotic behavior of logistic map in superior orbit and an improved chaos-based traffic control model, Nonlinear Dyn., 2018, 94(2), 959–975. doi: 10.1007/s11071-018-4403-y [3] Ashish and J. Cao, A novel fixed point feedback approach studying the dynamcial behaviour of standard logistic map, Int. J. Bifurc. Chaos, 2019, 29(1), 16. [4] Ashish, J. Cao and R. Chugh, Controlling chaos using superior feedback technique with applications in discrete traffic models, Int. J. Fuzzy Syst., 2019, 21(5), 1467–1479. doi: 10.1007/s40815-019-00636-8 [5] Ashish, J. Cao and R. Chugh, Discrete chaotification in modulated logistic system, Int. J. Bifurc. Chaos, 2021, 31(5), 14. [6] Ashish, J. Cao, F. Alsaadi and A. K. Malik, Discrete Superior Hyperbolicity in Chaotic Maps, Chaos: Theory and Applications, 2021, 3(1), 34–42. doi: 10.51537/chaos.936679 [7] Ashish, J. Cao and F. Alsaadi, Chaotic Evolution of Difference Equations in Mann Orbit, J. Appl. Anal. Comput., 2021, 11(6), 3063–3082. [8] Ashish and J. Cao, Dynamical interpretations of a generalized cubic map, J. Appl. Anal. Comput., 2022, 12(6), 2314–2329. [9] D. Baleanu, G. Wu, Y. Bai and F. Chen, Stability analysis of Caputo–like discrete fractional systems, Commun. Nonlinear Sci. Numer. Simulat., 2017, 48, 520–530. doi: 10.1016/j.cnsns.2017.01.002 [10] S. Boccaletti, C. Grebogi, Y. Lai, H. Mancini and D Maza, The control of chaos: theory and applications, Phys. Rep., 2000, 329, 103–197. doi: 10.1016/S0370-1573(99)00096-4 [11] P. Carmona and D. Franco, Control of chaotic behavior and prevention of extinction using constant proportional feedback, Nonlinear Anal. RWA, 2011, 12, 3719–3726. [12] R. Chugh, M. Rani and Ashish, Logistic map in Noor orbit, Chaos and Complexity Letters, 2012, 6(3), 167–175. [13] Q. Chen and J. Gao, Delay feedback control of the Lorenz-like system, Math. Probl. Eng., 2018, 1–13. [14] M. De Sousa Vieira and A. J. Lichtenberg, Controlling chaos using nonlinear feedback with delay, Phys. Rev. E, 1996, 54, 1200–1207. doi: 10.1103/PhysRevE.54.1200 [15] R. L. Devaney, A First Course in Chaotic Dynamical Systems: Theory and Experiment, Addison-Wesley, 1992. [16] J. E. Disbro and M. Frame, Traffic flow theory and chaotic behavior, Transp. Res. Rec., 1990, 1225, 109–115. [17] W. L. Ditto, S. N. Rauseo and M. L. Spano, Experimental control of chaos, Phys. Rev. Lett., 1991, 65(26), 3211–3214. [18] S. Elaydi, An Introduction to Difference Equations, Springer New York, NY, 2005. [19] A. Garfinkel, M. L. Spano, W. L. Ditto and J. N. Weiss, Controlling cardiac chaos, Science, 1992, 257, 1230–1235. doi: 10.1126/science.1519060 [20] D. Grether, A. Neumann and K. Nagel, Simulation of urban traffic control: A queue model approach, Procedia Comput. Sci., 2012, 10, 808–814. doi: 10.1016/j.procs.2012.06.104 [21] D. Jarrett and Y. Zhang, The dynamic behavior of road traffic flow: stability or chaos?, Applications of Fractals and Chaos: The Shape of Things, Springer Verlag, Berlin, 1993. [22] G. Jiang and W. Zheng, A simple method of chaos control for a class of chaotic discrete-time systems, Chaos Solitons Fractals, 2005, 23, 843–849. doi: 10.1016/j.chaos.2004.05.025 [23] M. Mukherjee and S. Halderb, Stabilization and control of chaos based on nonlinear dynamic Inversion, Energy Procedia, 2017, 117, 731–738. doi: 10.1016/j.egypro.2017.05.188 [24] M. A. Noor, New approximation schemes for general variational inequalities, J. Maths. Anal. Appl., 2000, 251, 217–229. doi: 10.1006/jmaa.2000.7042 [25] M. A. Noor, Some developments in general variational inequalities, Appl. Math. Comput., 2004, 251, 199–277. [26] M. A. Noor, K. I. Noor and M. T. Rassias, New trends in general variational inequalitiesm, Acta Appl. Mathemat., 2020, 170(1), 981–1064. doi: 10.1007/s10440-020-00366-2 [27] E. Ott, Chaos in dynamical systems, Cambridge University Press, 2nd ed., 2002. [28] E. Ott, C. Grebogi and J. A. Yorke, Controlling chaos, Phys. Rev. Lett., 1990, 64, 1196–1199. doi: 10.1103/PhysRevLett.64.1196 [29] H. S. Panigoro, M. Rayungsari and A. Suryanto, Bifurcation and chaos in a discrete-time fractional-order logistic modelwith Allee effect and proportional harvesting, J. Dyn. Control., 2023. https://doi.org/10.1007/s40435-022-01101-5. doi: 10.1007/s40435-022-01101-5 [30] S. Parthasarathy and S. Sinha, Controlling chaos in unidimensional maps using constant feedback, Phy. Rev. E, 1995, 51, 6239–6242. doi: 10.1103/PhysRevE.51.6239 [31] B. Peng, V. Petrov and K. Showalter, Controlling chemical chaos, J. Phys. Chem., 1991, 95, 4957–4959. doi: 10.1021/j100166a013 [32] B. T. Polyak, Chaos stabilization by predictive control, Autom. Remote Control, 2005, 66, 1791–1804. doi: 10.1007/s10513-005-0213-z [33] K. Pyragas, Continuous control of chaos by self-controlling feedback, Phys. Lett., 1992, 170A, 421–428. [34] A. G. Radwan, K. Moaddy, K. N. Salama, S. Momani and I. Hashim, Control and switching synchronization of fractional order chaotic systems using active control technique, J. Adv. Res., 2014, 05, 125–132. doi: 10.1016/j.jare.2013.01.003 [35] Renu, Ashish and R. Chugh, On the dynamics of a discrete difference map in Mann orbit, Comput. Appl. Math., 2022, 226(41), 1–19. [36] H. Sadeghian, K. Merat, H. Salarieh and A. Alasty, On the fuzzy minimum entropy control to stabilize the unstable fixed points of chaotic maps, Appl. Math. Model., 2011, 35(3), 1016–1023. doi: 10.1016/j.apm.2010.07.036 [37] H. Salarieh and A. Alasty, Chaos control in uncertain dynamical systems using nonlinear delayed feedback, Chaos Solitons Fractals, 2009, 41, 67–71. doi: 10.1016/j.chaos.2007.11.007 [38] H. Salarieh and A. Alasty, Stabilizing unstable fixed points of chaotic maps via minimum entropy control, Chaos Solitons Fractals, 2008, 37, 763–769. doi: 10.1016/j.chaos.2006.09.062 [39] H. G. Schuster and M. B. Stemmler, Control of chaos by oscillating feedback, Phy. Rev. E, 1997, 56, 6410–6417. doi: 10.1103/PhysRevE.56.6410 [40] P. Shang, X. Li and S. Kame, Chaotic analysis of traffic time series, Chaos Solitons Fractals, 2005, 25, 121–128. doi: 10.1016/j.chaos.2004.09.104 [41] S. Sinha, Controlling chaos in biology, Curr. Sci., 1997, 73(11), 977–983. [42] J. Singer and H. H. Bau, Active control of convection, Phys. Fluids, 1991, 3(12), 2859–2865. doi: 10.1063/1.857831 [43] T. Ushio and S. Yamamoto, Prediction-based control of chaos, Phys Lett. A, 1999, 13(1), 34–35. [44] J. N. Weiss, A. Garfinkel, M. L. Spano and W. L. Ditto, Chaos and chaos control in biology, J. Clin. Invest., 1994, 93, 1355–1360. doi: 10.1172/JCI117111 -
-
Figures(3) / Tables(1)
Export File
Citation
Ashish, Jinde Cao, Muhammad Aslam Noor. STABILIZATION OF FIXED POINTS IN CHAOTIC MAPS USING NOOR ORBIT WITH APPLICATIONS IN CARDIAC ARRHYTHMIA[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2452-2470. doi: 10.11948/20220350
Format
Content
DownLoad:
-
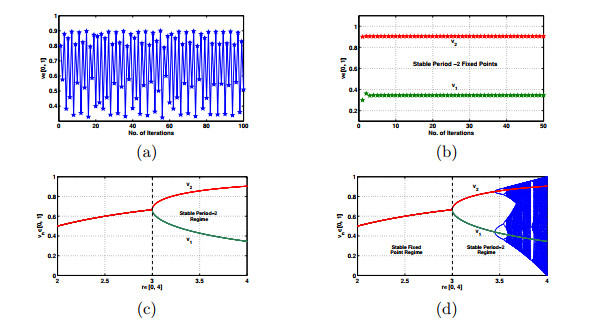
Figure 1.
(a) Unstable fixed point plot for an original map
$ \phi_4(v)=4v(1-v) $ $ \phi_4(v)=4v(1-v) $ $ N=50 $ $ \alpha = 0.4, \beta = 0.3 $ $ \gamma = 0.3 $ $ \alpha = 0.4, \beta = 0.3 $ $ \gamma = 0.3 $ -
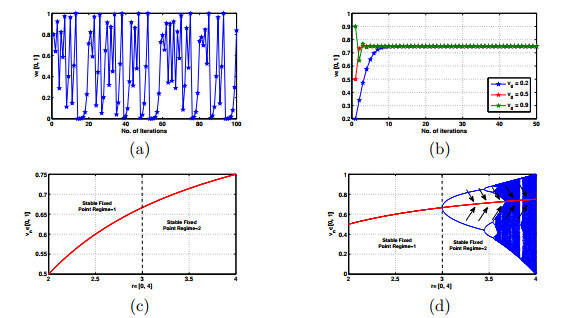
Figure 2.
(a) Unstable periodic point plot for an original map
$ \phi_4(v)=4v(1-v) $ $ \phi^2_4(v) $ $ N=50 $ $ \alpha = 0.3, \beta = 0.2 $ $ \gamma = 0.2 $ $ \alpha = 0.3, \beta = 0.2 $ $ \gamma = 0.2 $ -
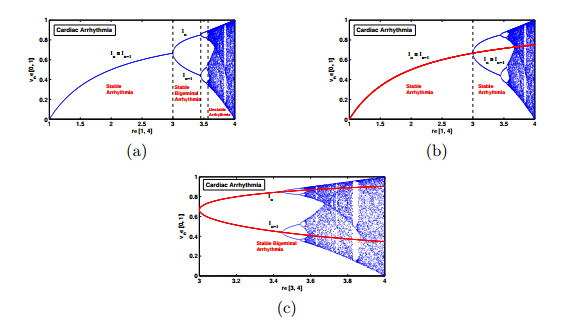
Figure 3.
(a) Bifurcation plot for the Cardiac Arrhythmia model
$ I_{n} = r I_{n-1}(1-I_{n-1}) $ $ \alpha = 0.4 $ $ \beta = 0.3 $ $ \gamma = 0.3 $ $ r\in[1, 4] $ $ \alpha = 0.3 $ $ \beta = 0.2 $ $ \gamma = 0.2 $ $ r\in[3, 4] $