| Citation: | Fuchen Zhang, Fei Xu. DYNAMICAL BEHAVIOR OF THE GENERALIZED COMPLEX LORENZ CHAOTIC SYSTEM[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 1915-1931. doi: 10.11948/20220364 |
DYNAMICAL BEHAVIOR OF THE GENERALIZED COMPLEX LORENZ CHAOTIC SYSTEM
-
Abstract
The purpose of this paper is to investigate the boundedness and global attractivity of the complex Lorenz system:
$\dot x = \alpha \left( {y - x} \right),\dot y = \gamma x - cy - dxz,\dot z = - \beta z + \frac{1}{2}\left( {\bar xy + x\bar y} \right),$
where $ \alpha,\beta,\gamma,c,d $ are real parameters, $ x $ and $ y $ are complex variables, $ z $ is a real variable, an overbar denotes complex conjugate variable and dots represent derivatives with respect to time. This system arises in many important applications in laser physics and rotating fluids dynamics. It is very interesting that we find that this system exhibits chaos phenomenon for the given parameters. Using generalized Lyapunov-like functions, we prove the existence of the ultimate bound set and the globally exponentially attractive set in this generalized complex Lorenz system. The rate of the trajectories is also obtained. Numerical simulations show the effectiveness and correctness of the conclusions. Finally, we present an application of our results that obtained in this paper.
-

-
References
[1] C. Chen, J. Cao and X. Zhang, The topological structure of the Rabinovich system having an invariant algebraic surface, Nonlinearity, 2008, 21, 211–220. doi: 10.1088/0951-7715/21/2/002 [2] G. Chen and T. Ueta, Yet another chaotic attractor, Int. J. Bifurc. Chaos Appl. Sci. Eng., 1999, 9, 1465–1466. doi: 10.1142/S0218127499001024 [3] H. K. Chen, Synchronization of two different chaotic systems: A new system and each of the dynamical systems Lorenz, Chen and Lu, Chaos, Solitons Fractals, 2005, 25, 1049–1056. doi: 10.1016/j.chaos.2004.11.032 [4] L. Chua, M. Komuro and T. Matsumoto, The double scroll family, IEEE Trans. Circuits Syst., 1986, 33(11), 1072–1118. doi: 10.1109/TCS.1986.1085869 [5] A. C. Fowler, J. D. Gibbon and M. J. McGuinness, The complex Lorenz equations, Physica D., 1982, 4, 139–163. doi: 10.1016/0167-2789(82)90057-4 [6] A. C. Fowler, J. D. Gibbon and M. J. McGuinness, The real and complex Lorenz equations and their relevance to physical systems, Physica D: Nonlinear Phenomena, 1983, 7(1–3), 126–134. doi: 10.1016/0167-2789(83)90123-9 [7] P. Frederickson, J. Kaplan, E. Yorke and J. Yorke, The Lyapunov dimension of strange attractors, J. Differ. Equ., 1983, 49(2), 185–207. doi: 10.1016/0022-0396(83)90011-6 [8] J. D. Gibbon and M. J. McGuinness, The real and complex Lorenz equations in rotating fluids and lasers, Physica D: Nonlinear Phenomena, 1982, 5(1), 108–122. doi: 10.1016/0167-2789(82)90053-7 [9] N. V. Kuznetsov, The Lyapunov dimension and its estimation via the Leonov method, Phys. Lett. A, 2016, 380(25–26), 2142–2149. doi: 10.1016/j.physleta.2016.04.036 [10] N. V. Kuznetsov, Theory of hidden oscillations and stability of control systems, J. Comput. Syst. Sci. Int., 2020, 59, 647–668. doi: 10.1134/S1064230720050093 [11] N. Kuznetsov, G. Leonov, T. Mokaev, A. Prasad and M. Shrimali, Finite-time Lyapunov dimension and hidden attractor of the Rabinovich system, Nonlinear Dyn., 2018, 92(2), 267–285. doi: 10.1007/s11071-018-4054-z [12] N. Kuznetsov, T. Mokaev, O. Kuznetsova, et al., The Lorenz system: Hidden boundary of practical stability and the Lyapunov dimension, Nonlin. Dyn., 2020, 102, 713–732. doi: 10.1007/s11071-020-05856-4 [13] N. Kuznetsov, T. Mokaev, V. Ponomarenko, E. Seleznev, N. Stankevich and L. Chua, Hidden attractors in Chua circuit: Mathematical theory meets physical experiments, Nonlinear Dyn., 2023, 111(6), 5859–5887. doi: 10.1007/s11071-022-08078-y [14] G. Leonov, Lyapunov dimension formulas for Henon and Lorenz attractors, St. Petersburg Math. J., 2001, 13, 1–12. [15] G. Leonov, Bounds for attractors and the existence of homoclinic orbits in the Lorenz system, J. Appl. Math. Mech., 2001, 65(1), 19–32. doi: 10.1016/S0021-8928(01)00004-1 [16] G. Leonov and V. Boichenko, Lyapunov's direct method in the estimation of the Hausdorff dimension of attractors, Acta Appl. Math., 1992, 26(1), 1–60. doi: 10.1007/BF00046607 [17] G. Leonov, A. Bunin and N. Koksch, Attractor localization of the Lorenz system, Z. Angew. Math. Mech., 1978, 67, 649–656. [18] G. Leonov and N. Kuznetsov, Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits, Int. J. Bifurc. Chaos Appl. Sci. Eng., 2013, 23, 1330002. doi: 10.1142/S0218127413300024 [19] G. Leonov, N. Kuznetsov and T. Mokaev, Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion, Eur. Phys. J. Spec. Top., 2015, 224(8), 1421–1458. doi: 10.1140/epjst/e2015-02470-3 [20] G. Leonov, N. Kuznetsov and V. Vagaitsev, Hidden attractor in smooth Chua systems, Physica D., 2012, 41(18), 1482–1486. [21] X. Liao, Y. Fu, S. Xie and P. Yu, Globally exponentially attractive sets of the family of Lorenz systems, Sci. China, Ser. F., 2008, 51(3), 283–292. [22] S. Liu and P. Liu, Adaptive anti-synchronization of chaotic complex nonlinear systems with unknown parameters, Nonlinear Analysis: Real World Applications, 2011, 12, 3046–3055. doi: 10.1016/j.nonrwa.2011.05.006 [23] E. Lorenz, Deterministic nonperiodic flow, J. Atmos. Sci., 1963, 20, 130–141. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [24] J. Lu and G. Chen, A new chaotic attractor coined, Int. J. Bifurc. Chaos Appl. Sci. Eng., 2002, 12(3), 659–661. doi: 10.1142/S0218127402004620 [25] E. E. Mahmoud, Dynamics and synchronization of new hyperchaotic complex Lorenz system, Mathematical and Computer Modelling, 2012, 55(7–8), 1951–1962. doi: 10.1016/j.mcm.2011.11.053 [26] G. M. Mahmoud, M. E. Ahmed and E. E. Mahmoud, Analysis of hyperchaotic complex Lorenz systems, International Journal of Modern Physics C, 2008, 19(10), 1477–1494. doi: 10.1142/S0129183108013151 [27] G. M. Mahmoud, M. A. Al-Kashif and S. A. Aly, Basic properties and chaotic synchronization of complex Lorenz system, International Journal of Modern Physics C, 2007, 18(02), 253–265. doi: 10.1142/S0129183107010425 [28] G. M. Mahmoud, M. A. Al-Kashif and A. A. Farghaly, Chaotic and hyperchaotic attractors of a complex nonlinear system, J. Phys. A: Math. Theor., 2008, 41(5), 055104. doi: 10.1088/1751-8113/41/5/055104 [29] W. Qin and G. Chen, On the boundedness of solutions of the Chen system, J. Math. Anal. Appl., 2007, 329(11), 445–451. [30] A. Rauh, L. Hannibal and N. B. Abraham, Global stability properties of the complex Lorenz model, Physica D: Nonlinear Phenomena, 1996, 99(1), 45–58. doi: 10.1016/S0167-2789(96)00129-7 [31] H. Richter, Controlling the Lorenz system: Combining global and local schemes, Chaos, Solitons Fractals, 2001, 12(13), 2375–2380. doi: 10.1016/S0960-0779(00)00216-2 [32] O. Rossler, An equation for hyperchaos, Phys. Lett. A., 1979, 2–3, 155–157. [33] L. Stenflo, Generalized Lorenz equations for acoustic-gravity waves in the atmosphere, Phys. Scr., 1996, 3, 83–84. [34] F. Zhang, R. Chen, X. Wang, X. Chen, C. Mu and X. Liao, Dynamics of a new 5D hyperchaotic system of Lorenz type, Int. J. Bifurc. Chaos Appl. Sci. Eng., 2018, 28(3), 1850036. doi: 10.1142/S0218127418500360 [35] F. Zhang, Y. Li and C. Mu, Bounds of solutions of a kind of hyper-chaotic systems and application, J. Math. Res. Appl., 2013, 33(3), 345–352. [36] F. Zhang, X. Liao, C. Mu, G. Zhang and Y. Chen, On global boundedness of the Chen system, Discrete Contin. Dyn. Syst., Ser. B., 2017, 22(4), 1673–1681. [37] F. Zhang, X. Liao and G. Zhang, On the global boundedness of the Lu system, Appl. Math. Comput., 2016, 284, 332–339. [38] F. Zhang, X. Liao and G. Zhang, Some new results for the generalized Lorenz system, Qual. Theory Dyn. Syst., 2017, 16(3), 749–759. doi: 10.1007/s12346-016-0206-z [39] F. Zhang, X. Liao, G. Zhang and C. Mu, Dynamical analysis of the generalized Lorenz systems, J. Dyn. Control Syst., 2017, 23(2), 349–362. doi: 10.1007/s10883-016-9325-8 [40] F. Zhang, X. Liao, G. Zhang, C. Mu, P. Zhou and M. Xiao, Dynamical behaviors of a generalized Lorenz family, Discrete Contin. Dyn. Syst., Ser. B., 2017, 22(10), 3707–3720. [41] F. Zhang, S. Liu and W. Yu, Characteristics of time-delay complex Lorenz chaotic system and its self-synchronization of time delay, Acta Phys. Sin., 2013, 62(22), 220505. doi: 10.7498/aps.62.220505 [42] F. Zhang, C. Mu and X. Li, On the boundness of some solutions of the Lu system, Int. J. Bifurc. Chaos Appl. Sci. Eng., 2012, 22, 1250015. doi: 10.1142/S0218127412500150 -
-
-
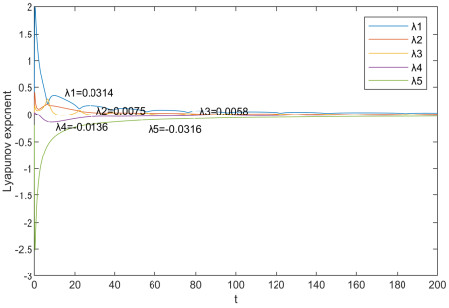
Figure 1.
Lyapunov exponents of system (2.2).
-
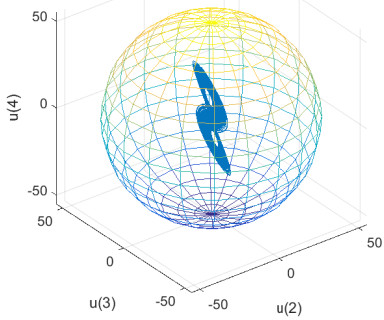
Figure 2.
Projection of
$ {\Omega _{1,1}} $ $ \left( {{u_2},{u_3},{u_4}} \right) $ -
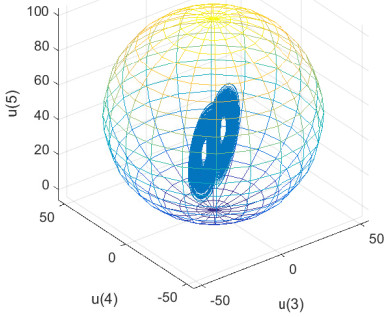
Figure 3.
Projection of
$ {\Omega _{1,1}} $ $ \left( {{u_3},{u_4},{u_5}} \right) $ -
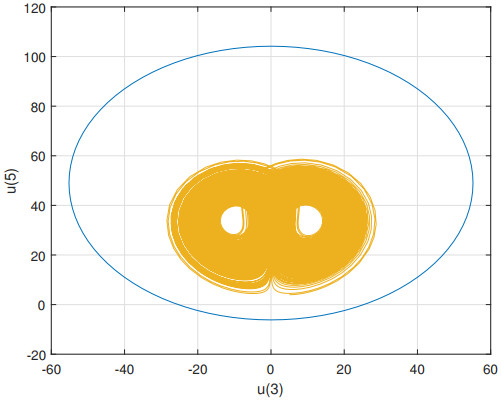
Figure 4.
Projection of
$ {\Omega _{1,1}} $ $ ( {{u_3},{u_5}}) $ -
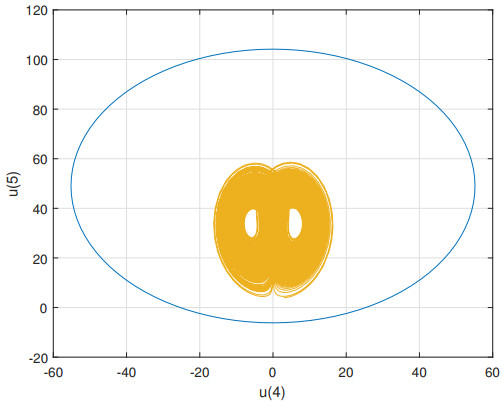
Figure 5.
Projection of
$ {\Omega _{1,1}} $ $ ( {{u_4},{u_5}}) $




 DownLoad:
DownLoad: