| Citation: |
Yahong Peng, Yujing Li. STABILITY AND HOPF BIFURCATION OF A DELAYED PREDATOR-PREY SYSTEM WITH NONLOCAL COMPETITION AND HERD BEHAVIOUR[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 1932-1958. doi: 10.11948/20220422
|
STABILITY AND HOPF BIFURCATION OF A DELAYED PREDATOR-PREY SYSTEM WITH NONLOCAL COMPETITION AND HERD BEHAVIOUR
-
Abstract
In this paper, we investigate the stability and Hopf bifurcation of a diffusive predator-prey system with herd behaviour. The model is described by introducing both time delay and nonlocal prey intraspecific competition. Compared to the model without time delay, or without nonlocal competition, thanks to the together action of time delay and nonlocal competition, we prove that the first critical value of Hopf bifurcation may be homogenous or non-homogeneous. We also show that a double-Hopf bifurcation occurs at the intersection point of the homogenous and non-homogeneous Hopf bifurcation curves. Furthermore, by the computation of normal forms for the system near equilibria, we investigate the stability and direction of Hopf bifurcation. Numerical simulations also show that the spatially homogeneous and non-homogeneous periodic patters.
-
Keywords:
- Predator-prey model /
- time delay /
- nonlocal prey competition /
- Hopf bifurcation
-
-
References
[1] V. Ajraldi, M. Pittavino and E. Venturino, Modeling herd behavior in population systems, Nonlinear Anal. -Real World Appl., 2011, 12(4), 2319–2338. doi: 10.1016/j.nonrwa.2011.02.002 [2] M. Banerjee and V. Volpert, Prey-predator model with a nonlocal consumption of prey, Chaos, 2016, 26(8), 083120. doi: 10.1063/1.4961248 [3] A. Bayliss and V. A. Volpert, Complex predator invasion waves in a holling-tanner model with nonlocal prey interaction, Physica D, 2017, 346, 37–58. doi: 10.1016/j.physd.2017.02.003 [4] P. A. Braza, Predator-prey dynamics with square root functional responses, Nonlinear Anal. -Real World Appl., 2012, 13(4), 1837–1843. doi: 10.1016/j.nonrwa.2011.12.014 [5] N. F. Britton, Spatial structures and periodic travelling waves in an integro-differential reaction-diffusion population model, SIAM J. Appl. Math., 1990, 50(6), 1663–1688. doi: 10.1137/0150099 [6] T. Faria, Normal forms and Hopf bifurcation for partial differential equations with delays, Trans. Am. Math. Soc., 2000, 352(5), 2217–2238. doi: 10.1090/S0002-9947-00-02280-7 [7] M. A. Fuentes, M. N. Kuperman and V. M. Kenkre, Nonlocal interaction effects on pattern formation in population dynamics, Phys. Rev. Lett., 2003, 91(15), 158104. doi: 10.1103/PhysRevLett.91.158104 [8] J. Furter and M. Grinfeld, Local vs. non-local interactions in population dynamics, J. Math. Biol., 1989, 27(1), 65–80. doi: 10.1007/BF00276081 [9] Z. Ge and Y. He, Diffusion effect and stability analysis of a predator-prey system described by a delayed reaction-diffusion equations, J. Math. Anal. Appl., 2008, 339(2), 1432–1450. doi: 10.1016/j.jmaa.2007.07.060 [10] W. Ni, J. Shi and M. Wang, Global stability and pattern formation in a nonlocal diffusive Lotka-Volterra competition model, J. Differ. Equ., 2018, 264(11), 6891–6932. doi: 10.1016/j.jde.2018.02.002 [11] S. Pal, S. Ghorai and M. Banerjee, Analysis of a prey-predator model with non-local interaction in the prey population, Bull. Math. Biol., 2018, 80(4), 906–925. doi: 10.1007/s11538-018-0410-x [12] Y. Peng and K. Yu, Turing pattern of a diffusive predator-prey model with nonlocal delay and herd behavior, J. Math. Anal. Appl., 2023, 527(1), 127346. doi: 10.1016/j.jmaa.2023.127346 [13] Y. Peng and G. Zhang, Dynamics analysis of a predator-prey model with herd behavior and nonlocal prey competition, Math. Comput. Simulat., 2020, 170, 366–378. doi: 10.1016/j.matcom.2019.11.012 [14] Y. Song, Y. Peng and T. Zhang, The spatially inhomogeneous Hopf bifurcation induced by memory delay in a memory-based diffusion system, J. Differ. Equ., 2021, 300, 597–624. doi: 10.1016/j.jde.2021.08.010 [15] Y. Song, Y. Peng and X. Zou, Persistence, stability and Hopf bifurcation in a diffusive ratio-dependent predator-prey model with delay, Int. J. Bifurcation Chaos, 2014, 24(7), 1450093. doi: 10.1142/S021812741450093X [16] Y. Song and Q. Shi, Stability and bifurcation analysis in a diffusive predator-prey model with delayed and spatial average, Math. Meth. Appl. Sci., 2023, 46(5), 5561–5584. doi: 10.1002/mma.8853 [17] Y. Song, H. Wang and J. Wang, Cognitive consumer-resource spatiotemporal dynamics with nonlocal perception, J. Nonlinear Sci., 2024, 34(1), 19. doi: 10.1007/s00332-023-09996-w [18] Y. Su, J. Wei and J. Shi, Hopf bifurcations in a reaction-diffusion population model with delay effect, J. Differ. Equ., 2009, 247(4), 1156–1184. doi: 10.1016/j.jde.2009.04.017 [19] X. Tang and Y. Song, Stability, Hopf bifurcations and spatial patterns in a delayed diffusive predator-prey model with herd behavior, Appl. Math. Comput., 2015, 254, 375–391. [20] M. Wang, Stability and Hopf bifurcation for a prey-predator model with prey-stage structure and diffusion, Math. Biosci., 2008, 212(2), 149–160. doi: 10.1016/j.mbs.2007.08.008 [21] R. Wang and W. Zhao, Extinction and stationary distribution of a stochastic predator-prey model with Holling Ⅱ functional response and stage structure of prey, J. Appl. Anal. Comput., 2022, 12(1), 50–68. [22] W. Wang, L. Zhang, H. Wang and Z. Li, Pattern formation of a predator-prey system with Ivlev-type functional response, Ecol. Model., 2010, 221(2), 131–140. doi: 10.1016/j.ecolmodel.2009.09.011 [23] S. Wu and Y. Song, Stability and spatiotemporal dynamics in a diffusive predator-prey model with nonlocal prey competition, Nonlinear Anal. -Real World Appl., 2019, 48, 12–39. doi: 10.1016/j.nonrwa.2019.01.004 [24] X. Yan, Stability and Hopf bifurcation for a delayed prey-predator system with diffusion effects, Appl. Math. Comput., 2007, 192(2007), 552–566. [25] F. Yi, J. Wei and J. Shi, Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system, J. Differ. Equ., 2009, 246(5), 1944–1977. doi: 10.1016/j.jde.2008.10.024 [26] S. Yuan, C. Xu and T. Zhang, Spatial dynamics in a predator-prey model with herd behavior, Chaos, 2013, 23(3), 033102. doi: 10.1063/1.4812724 [27] X. Zhao, Global attractivity in a class of nonmonotone reaction-diffusin equations with time delay, Can. Appl. Math. Q., 2009, 17(1), 271–281. [28] C. Zhu and Y. Peng, Stability and bifurcation analysis in a nonlocal diffusive predator-prey model with hunting cooperation, J. Nonl. Model. Anal., 2023, 5(1), 95–107. [29] W. Zuo and J. Wei, Stability and Hopf bifurcation in a diffusive predator-prey system with delay effect, Nonlinear Anal. -Real World Appl., 2011, 12(4), 1998–2011. doi: 10.1016/j.nonrwa.2010.12.016 -
-
Figures(5)
Export File
Citation
Yahong Peng, Yujing Li. STABILITY AND HOPF BIFURCATION OF A DELAYED PREDATOR-PREY SYSTEM WITH NONLOCAL COMPETITION AND HERD BEHAVIOUR[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 1932-1958. doi: 10.11948/20220422
Format
Content
DownLoad:
-
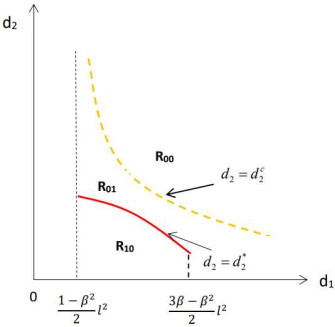
Figure 1.
The distribution of the first Hopf bifurcation value
$ \tau_{*} $ $ d_{1}-d_{2} $ $ d_2=d_{2}^{*} $ $ d_2=d_{2}^{c} $ $ \tau_{*}=\tau_{10} $ $ R_{10} $ $ \tau_{*}=\tau_{00} $ $ R_{0} $ -
Figure 2.
Bifurcation curves diagram for the system (1.5). Parameter values are
$ d_1=1,\; \beta=0.8,\; r=3,\; l=1.5 $ -
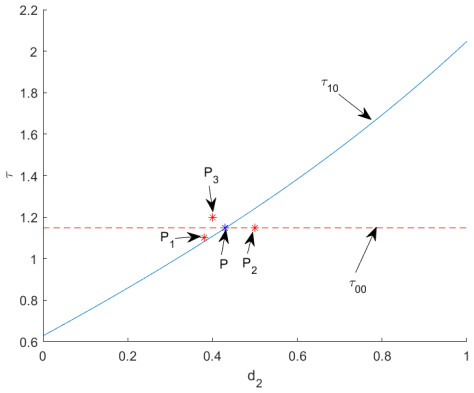
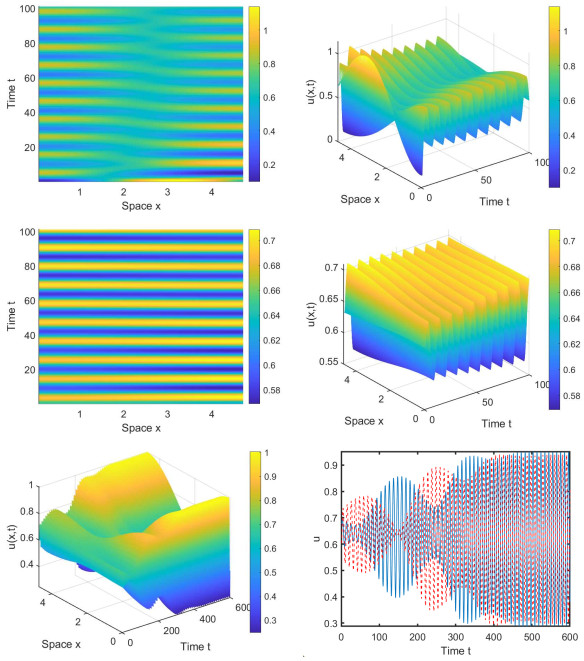
Figure 3.
The simulations for species
$ u $ $ d_1=1, \beta=0.8, r=3, l=1.5 $ $ d_2=0.38, \tau=1.1 $ $ P_{1} $ $ u(x,t)=0.64-0.5cos(0.5x), v(x,t)=0.2304-0.1cos(0.5x) $ $ t\in[-\tau,0] $ $ d_2=0.5, \tau=1.15 $ $ P_{2} $ $ u(x,t)=0.64+0.01cos(0.5x), v(x,t)=0.2304+0.01cos(0.5x) $ $ t\in[-\tau,0] $ $ d_2=0.4, \tau=1.2 $ $ P_{3} $ $ u(x,t)=0.64+0.05cos(0.5x), v(x,t)=0.2304+0,01cos(0.5x) $ $ t\in[-\tau,0]. $ $ x=0.785, $ $ x=3.925, $ -
Figure 4.
Bifurcation curves diagram for the system (1.5). Parameter values are
$ d_1=3,\; \beta=0.8,\; r=3,\; l=1.5 $ -
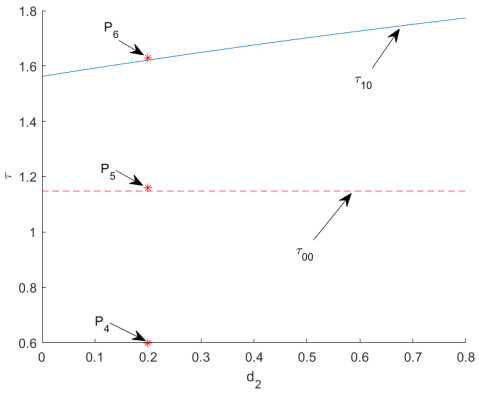
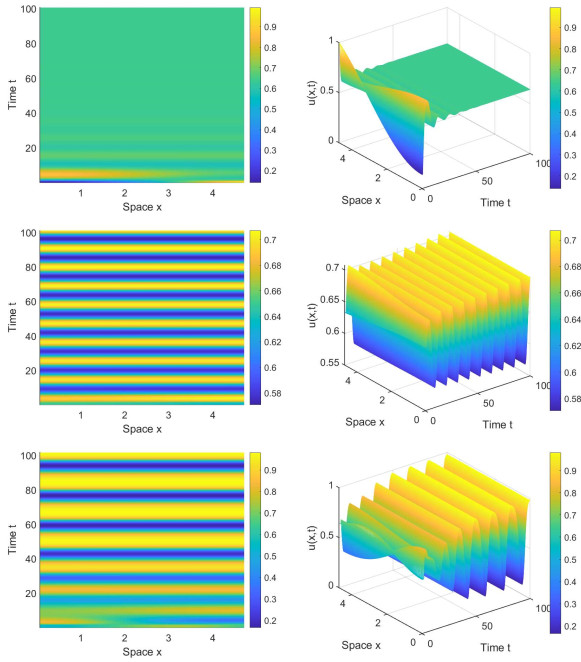
Figure 5.
The simulations for species
$ u $ $ d_1=3, \beta=0.8, r=3, l=1.5 $ $ d_2=0.2,\; \tau=0.6 $ $ P_{4} $ $ u(x,t)=0.64-0.5cos(0.5x), v(x,t)=0.2304-0.1cos(0.5x) $ $ t\in[-\tau,0] $ $ d_2=0.2, \tau=1.16 $ $ P_{5} $ $ u(x,t)=0.64+0.01cos(0.5x), v(x,t)=0.2304+0.01cos(0.5x) $ $ t\in[-\tau,0]; $ $ d_2=0.2, \tau=1.63 $ $ P_{6} $ $ u(x,t)=0.64-0.1cos(x), v(x,t)=0.2304-0.5cos(x) $ $ t\in[-\tau,0] $