| Citation: |
Mohammad Prawesh Alam, Geetan Manchanda, Arshad Khan. AN ε-UNIFORMLY CONVERGENT METHOD FOR SINGULARLY PERTURBED PARABOLIC PROBLEMS EXHIBITING BOUNDARY LAYERS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2089-2120. doi: 10.11948/20220382
|
AN ε-UNIFORMLY CONVERGENT METHOD FOR SINGULARLY PERTURBED PARABOLIC PROBLEMS EXHIBITING BOUNDARY LAYERS
-
Abstract
A numerical method is proposed for singularly perturbed parabolic convection-diffusion equation whose solution exhibits boundary layers near the right endpoints of the domain of consideration. The method encompasses the Crank-Nicolson scheme on a uniform mesh in temporal direction and quartic B-spline collocation method on piecewise-uniform (i.e., Shishkin mesh) mesh in space directions, respectively. Through rigorous convergence analysis, the method has shown theoretically fourth-order convergent in space direction and second-order convergent in the time direction. We have solved two numerical examples to prove the efficiency and robustness of the method and to validate the theoretical results. Since the exact/analytical solution to the problem is not known, hence we applied the double mesh principle to compute the maximum absolute errors. Additionally, some numerical simulations are displayed to produce the conclusiveness of determining layer behaviour and their locations.
-
-
References
[1] M. P. Alam, T. Begum and A. Khan, A new spline algorithm for solving non-isothermal reaction diffusion model equations in a spherical catalyst and spherical biocatalyst, Chemical Physics Letters, 2020, 754, 137651. doi: 10.1016/j.cplett.2020.137651 [2] M. P. Alam, T. Begum and A. Khan, A high-order numerical algorithm for solving lane-emden equations with various types of boundary conditions, Computational and Applied Mathematics, 2021, 40, 1-28. doi: 10.1007/s40314-020-01383-5 [3] M. P. Alam and A. Khan, A new numerical algorithm for time-dependent singularly perturbed differential-difference convection-diffusion equation arising in computational neuroscience, Computational and Applied Mathematics, 2022, 41(8), 402. doi: 10.1007/s40314-022-02102-y [4] M. P. Alam, A. Khan and D. Baleanu, A high-order unconditionally stable numerical method for a class of multi-term time-fractional diffusion equation arising in the solute transport models, International Journal of Computer Mathematics, 2023, 100(1), 105-132. doi: 10.1080/00207160.2022.2082248 [5] M. P. Alam, D. Kumar and A. Khan, Trigonometric quintic $B$-spline collocation method for singularly perturbed turning point boundary value problems, International Journal of Computer Mathematics, 2021, 98(5), 1029-1048. doi: 10.1080/00207160.2020.1802016 [6] C. Clavero, J. Jorge and F. Lisbona, A uniformly convergent scheme on a nonuniform mesh for convection-diffusion parabolic problems, Journal of Computational and Applied Mathematics, 2003, 154(2), 415-429. doi: 10.1016/S0377-0427(02)00861-0 [7] C. de Boor, On the convergence of odd-degree spline interpolation, Journal of approximation theory, 1968, 1(4), 452-463. doi: 10.1016/0021-9045(68)90033-6 [8] P. Farrell, A. Hegarty, J. M. M. Miller, et al., Robust computational techniques for boundary layers, CRC Press, 2000. [9] D. Fyfe, Linear dependence relations connecting equal interval n th degree splines and their derivatives, IMA Journal of Applied Mathematics, 1971, 7(3), 398-406. doi: 10.1093/imamat/7.3.398 [10] V. Gupta and M. K. Kadalbajoo, A layer adaptive B-spline collocation method for singularly perturbed one-dimensional parabolic problem with a boundary turning point, Numerical Methods for Partial Differential Equations, 2011, 27(5), 1143-1164. doi: 10.1002/num.20574 [11] C. Hall, On error bounds for spline interpolation, Journal of approximation theory, 1968, 1(2), 209-218. doi: 10.1016/0021-9045(68)90025-7 [12] C. Hirsch, Numerical computation of internal & external flows: fundamentals of numerical discretization, John Wiley & Sons, Inc., 1988. [13] M. Jacob, Heat Transfer, Wiley, New York, 1959. [14] M. K. Kadalbajoo, V. Gupta and A. Awasthi, A uniformly convergent B-spline collocation method on a nonuniform mesh for singularly perturbed one-dimensional time-dependent linear convection-diffusion problem, Journal of Computational and Applied Mathematics, 2008, 220(1-2), 271-289. doi: 10.1016/j.cam.2007.08.016 [15] A. Khan and Shahna, Non-polynomial quadratic spline method for solving fourth order singularly perturbed boundary value problems, Journal of King Saud University-Science, 2019, 31(4), 479-484. doi: 10.1016/j.jksus.2017.08.006 [16] D. Kumar, A parameter-uniform scheme for the parabolic singularly perturbed problem with a delay in time, Numerical Methods for Partial Differential Equations, 2021, 37(1), 626-642. doi: 10.1002/num.22544 [17] D. Kumar and M. K. Kadalbajoo, A parameter-uniform numerical method for time-dependent singularly perturbed differential-difference equations, Applied Mathematical Modelling, 2011, 35(6), 2805-2819. doi: 10.1016/j.apm.2010.11.074 [18] D. Kumar and P. Kumari, Parameter-uniform numerical treatment of singularly perturbed initial-boundary value problems with large delay, Applied Numerical Mathematics, 2020, 153, 412-429. doi: 10.1016/j.apnum.2020.02.021 [19] S. Kumar, M. Kumar, Kuldeep, and M. Kumar., A robust numerical method for a two-parameter singularly perturbed time delay parabolic problem, Computational and Applied Mathematics, 2020, 39(3), 1-25. [20] O. A. Ladyzhenskaia, V. A. Solonnikov and N. N. Uraltseva, Linear and quasi-linear equations of parabolic type, American Mathematical Society, 1968. [21] A. Majumdar and S. Natesan, An uniform hybrid numerical scheme for a singularly perturbed degenerate parabolic convection-diffusion problem, International Journal of Computer Mathematics, 2019, 96(7), 1313-1334. doi: 10.1080/00207160.2018.1485896 [22] J. J. Miller, E. O'riordan and G. I. Shishkin, Fitted numerical methods for singular perturbation problems: error estimates in the maximum norm for linear problems in one and two dimensions, World scientific, 1996. [23] R. Mohanty, R. Kumar and V. Dahiya, Spline in tension methods for singularly perturbed one space dimensional parabolic equations with singular coefficients, Neural Parallel and Scientific Computations, 2012, 20(1), 81. [24] K. Mukherjee and S. Natesan, Parameter-uniform fractional step hybrid numerical scheme for 2D singularly perturbed parabolic convection-diffusion problems, Journal of Applied Mathematics and Computing, 2019, 60(1), 51-86. [25] S. Polak, C. Den Heijer, W. Schilders and P. Markowich, Semiconductor device modelling from the numerical point of view, International Journal for Numerical Methods in Engineering, 1987, 24(4), 763-838. doi: 10.1002/nme.1620240408 [26] M. H. Prd and H. F. O. Weinberger, Maximum principles in differential equations, Springer Science & Business Media, 2012. [27] J. I. Ramos, An exponentially-fitted method for singularly perturbed, one-dimensional, parabolic problems, Applied mathematics and computation, 2005, 161(2), 513-523. doi: 10.1016/j.amc.2003.12.046 [28] A. Raza and A. Khan, Non-uniform haar wavelet method for solving singularly perturbed differential difference equations of neuronal variability, Applications and Applied Mathematics: An International Journal (AAM), 2020, 15(3), 5. [29] A. Raza, A. Khan, P. Sharma and K. Ahmad, Solution of singularly perturbed differential difference equations and convection delayed dominated diffusion equations using haar wavelet, Mathematical Sciences, 2021, 15(2), 123-136. doi: 10.1007/s40096-020-00355-4 [30] P. Roul, A fast and accurate computational technique for efficient numerical solution of nonlinear singular boundary value problems, International Journal of Computer Mathematics, 2019, 96(1), 51-72. doi: 10.1080/00207160.2017.1417588 [31] S. K. Sahoo and V. Gupta, Second-order parameter-uniform finite difference scheme for singularly perturbed parabolic problem with a boundary turning point, Journal of Difference Equations and Applications, 2021, 27(2), 223-240. doi: 10.1080/10236198.2021.1887157 [32] M. Sakai and R. A. Usmani, On exponential splines, Journal of approximation theory, 1986, 47(2), 122-131. doi: 10.1016/0021-9045(86)90037-7 [33] S. Singh, D. Kumar and K. Deswal, Trigonometric B-spline based $\varepsilon$-uniform scheme for singularly perturbed problems with robin boundary conditions, Journal of Difference Equations and Applications, 2022, 28(7), 924-945. doi: 10.1080/10236198.2022.2099273 [34] M. Stynes and E. O'Riordan, Uniformly convergent difference schemes for singularly perturbed parabolic diffusion-convection problems without turning points, Numerische Mathematik, 1989, 55(5), 521-544. doi: 10.1007/BF01398914 [35] K. Surla and V. Jerkovic, Some possibilities of applying spline collocations to singular perturbation problems, Numerical Methods and Approximation Theory, 1985, 2, 19-25. [36] S. Yadav and P. Rai, An almost second order hybrid scheme for the numerical solution of singularly perturbed parabolic turning point problem with interior layer, Mathematics and Computers in Simulation, 2021, 185, 733-753. doi: 10.1016/j.matcom.2021.01.017 -
-
Figures(12) / Tables(5)
Export File
Citation
Mohammad Prawesh Alam, Geetan Manchanda, Arshad Khan. AN ε-UNIFORMLY CONVERGENT METHOD FOR SINGULARLY PERTURBED PARABOLIC PROBLEMS EXHIBITING BOUNDARY LAYERS[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 2089-2120. doi: 10.11948/20220382
Format
Content
DownLoad:
-
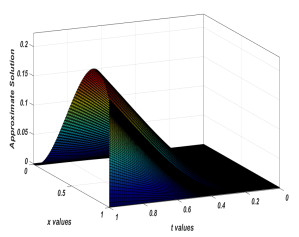
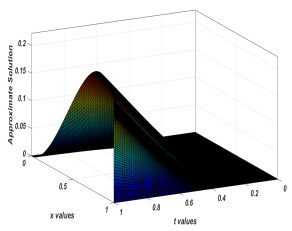
Figure 1.
Approximate solutions of the Problem 6.1 for
$ n = 128 $ $ \varepsilon= 2^{-10} $ -
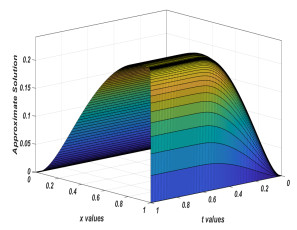
Figure 2.
Approximate solutions of the Problem 6.1 for
$ n = 128 $ $ \varepsilon= 2^{-20} $ -
Figure 3.
Loglog plot of errors the Problem 6.1 for
$ n = 128 $ $ \varepsilon= 2^{-10} $ -
Figure 4.
Loglog plot of errors of the Problem 6.1 for
$ n = 128 $ $ \varepsilon= 2^{-20} $ -
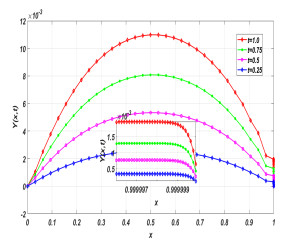
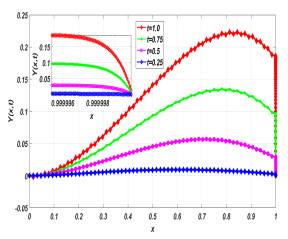
Figure 5.
Approximate solutions of the Problem 6.1 at various time level with
$ n = 64 $ $ \varepsilon= 2^{-20} $ -
Figure 6.
Approximate solutions of the Problem 6.1 at various time level with
$ n =128 $ $ \varepsilon= 2^{-20} $ -
Figure 7.
Approximate solutions of the Problem 6.2 for
$ n = 128 $ $ \varepsilon= 2^{-10} $ -
Figure 8.
Approximate solutions of the Problem 6.2 for
$ n = 128 $ $ \varepsilon= 2^{-20} $ -
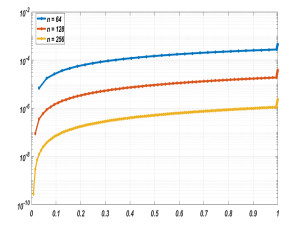
Figure 9.
Loglog plot of errors of the Problem 6.2 for
$ n = 64, 128, 256 $ $ \varepsilon= 2^{-10} $ -
Figure 10.
Loglog plot of errors of the Problem 6.2 for
$ n = 64, 128, 256 $ $ \varepsilon=2^{-20} $ -
Figure 11.
Approximate solutions of the Problem 6.2 at various time level with
$ n = 64 $ $ \varepsilon= 2^{-20} $ -
Figure 12.
Approximate solutions of the Problem 6.2 at various time level with
$ n =128 $ $ \varepsilon= 2^{-20} $