| Citation: | Ximing Fang, Ze Gu, Zhijun Qiao. CONVERGENCE OF THE TWO-POINT MODULUS-BASED MATRIX SPLITTING ITERATION METHOD[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2504-2521. doi: 10.11948/20220400 |
CONVERGENCE OF THE TWO-POINT MODULUS-BASED MATRIX SPLITTING ITERATION METHOD
-
Abstract
In this paper, we discuss the convergence of the two-point modulus-based matrix splitting iteration method for solving the linear complementarity problem. Some convergence conditions are presented from the spectral radius and the matrix norm when the system matrix is a $ P $-matrix. Besides, the quasi-optimal cases of the method are studied. Numerical experiments are provided to show the presented results.
-
Keywords:
- Linear complementarity problem /
- matrix splitting /
- convergence
-

-
References
[1] B. H. Ahn, Solution of nonsymmetric linear complementarity problems by iterative methods, J. Optim. Theory Appl., 1981, 33(2), 175–185. doi: 10.1007/BF00935545 [2] W. M. G. Bokhoven van, Piecewise-linear modelling and analysis, Technische Hogeschool Eindhoven, Eindhoven, 1981. [3] Z. Bai, Modulus-based matrix splitting iteration methods for linear complementarity problems, Numer. Linear Algebra Appl., 2010, 17(6), 917–933. doi: 10.1002/nla.680 [4] L. Cvetkovic, A. Hadjidimos and V. Kostic, On the choice of parameters in MAOR type splitting methods for the linear complementarity problem, Numer. Algorithms, 2014, 4(67), 793–806. [5] R. W. Cottle, J. Pang and R. E. Stone, The Linear Complementarity Problem, Academic Press, Inc., Bostion, MA, 1992. [6] C. W. Cryer, The solution of a quadratic programming problem using systematic over-relaxation, SIAM J. Control Optim., 1971, 9(3), 385–392. doi: 10.1137/0309028 [7] J. Dong and M. Jiang, A modified modulus method for symmetric positive-definite linear complementarity problems, Numer. Linear Algebra Appl., 2009, 16(2), 129–143. doi: 10.1002/nla.609 [8] P. Dai, J. Li, J. Bai and J. Qiu, A preconditioned two-step modulus-based matrix splitting iteration method for linear complementarity problem, Appl. Math. Comput., 2019, 348, 542–551. [9] A. Frommer and G. Mayer, Convergence of relaxed parallel multisplitting methods, Linear Algebra Appl., 1989, 119, 141–152. doi: 10.1016/0024-3795(89)90074-8 [10] A. Frommer and D. B. Szyld, H-splittings and two-stage iterative methods, Numer. Math., 1992, 63(1), 345–356. doi: 10.1007/BF01385865 [11] M. C. Ferris and J. Pang, Complementarity and Variational Problems, State of the Art, SIAM, Philadephia, Pennsylvania, 1997. [12] A. Hadjidimos and M. Tzoumas, Nonstationary extrapolated modulus algorithms for the solution of the linear complementarity problem, Linear Algebra Appl., 2009, 431(1–2), 197–210. doi: 10.1016/j.laa.2009.02.024 [13] A. Hadjidimos, M. Lapidakis and M. Tzoumas, On iterative solution for linear complementarity problem with an H+-matrix, SIAM J. Matrix Anal. Appl., 2012, 33(1), 97–110. doi: 10.1137/100811222 [14] M. Kojima, N. Megiddo and Y. Ye, An interior point potential reduction algorithm for the linear complementarity problem, Math. Program., 1992, 54(1–3), 267–279. doi: 10.1007/BF01586054 [15] S. Liu, H. Zheng and W. Li, A general accelerated modulus-based matrix splitting iteration method for solving linear complementarity problems, Calcolo, 2016, 53(2), 189–199. doi: 10.1007/s10092-015-0143-2 [16] W. Li, A general modulus-based matrix splitting method for linear complementarity problems of H-matrices, Appl. Math. Lett., 2013, 26(12), 1159–1164. doi: 10.1016/j.aml.2013.06.015 [17] I. Marek and D. B. Szyld, Comparison theorems for weak splittings of bounded operators, Numer. Math., 1990, 58(1), 387–397. doi: 10.1007/BF01385632 [18] K. G. Murty, Linear Complementarity, Linear and Nonlinear Programming, Heldermann Verlag, Berlin, 1988. [19] H. Ren, X. Wang, X. Tang and T. Wang, The general two-sweep modulus-based matrix splitting iteration method for solving linear complementarity problems, Comput. Math. Appl., 2019, 77, 1071–1081. doi: 10.1016/j.camwa.2018.10.040 [20] X. Shi, L. Yang and Z. Huang, A fixed point method for the linear complementarity problem arising from American option pricing, Acta Math. Appl. Sin., 2016, 32(4), 921–932. doi: 10.1007/s10255-016-0613-6 [21] S. Wu and C. Li, Two-sweep modulus-based matrix splitting iteration methods for linear complementarity problems, J. Comput. Appl. Math., 2016, 302, 327–339. doi: 10.1016/j.cam.2016.02.011 [22] S. Wu and C. Li, A generalized Newton method for non-Hermitian positive definite linear complementarity problem, Calcolo, 2017, 54(1), 43–56. doi: 10.1007/s10092-016-0175-2 [23] X. Wu, X. Peng and W. Li, A preconditioned general modulus-based matrix splitting iteration method for linear complementarity problems of H-matrices, Numer. Algorithms, 2018, 79(4), 1131–1146. doi: 10.1007/s11075-018-0477-3 [24] H. Zheng and W. Li, The modulus-based nonsmooth Newton¡¯s method for solving linear complementarity problems, J. Comput. Appl. Math., 2015, 288, 116–126. doi: 10.1016/j.cam.2015.04.006 [25] H. Zheng, W. Li and S. Vong, A relaxation modulus-based matrix splitting iteration method for solving linear complementarity problems, Numer. Algorithms, 2017, 74, 137–152. doi: 10.1007/s11075-016-0142-7 [26] L. Zhang, Two-step modulus-based matrix splitting iteration method for linear complementarity problems, Numer. Algorithms, 2011, 57(1), 83–99. doi: 10.1007/s11075-010-9416-7 [27] L. Zhang, Two-stage multisplitting iteration methods using modulus-based matrix splitting as inner iteration for linear complementarity problems, J. Optim. Theory Appl., 2014, 160(1), 189–203. doi: 10.1007/s10957-013-0362-0 [28] N. Zheng and J. Yin, Accelerated modulus-based matrix splitting iteration methods for linear complementarity problem, Numer. Algorithms, 2013, 64(2), 245–262. doi: 10.1007/s11075-012-9664-9 -
-
-
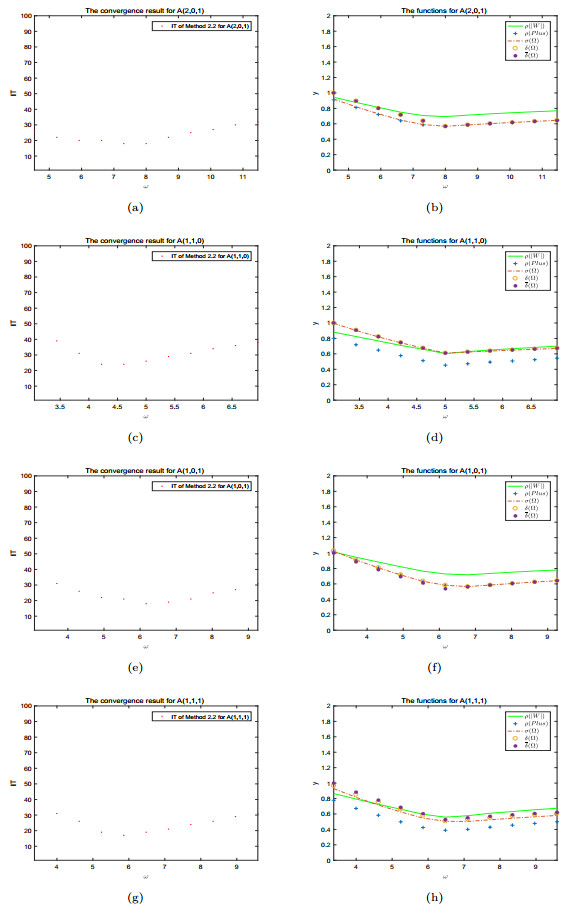
Figure 1.
The numerical results about IT and the convergence conditions
-
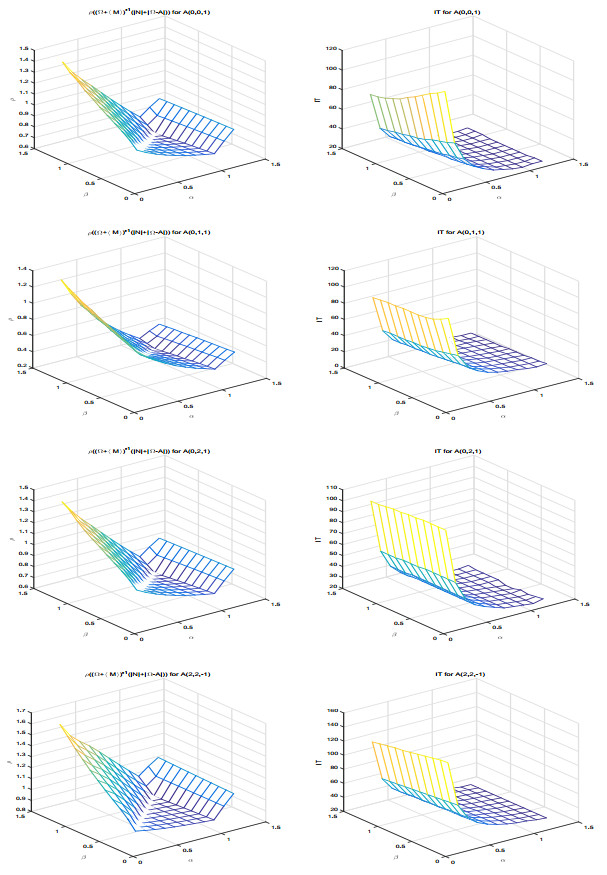
Figure 2.
The comparison between
$ \rho((\Omega+\langle M\rangle)^{-1}(|N|+|\Omega-A|)) $ -
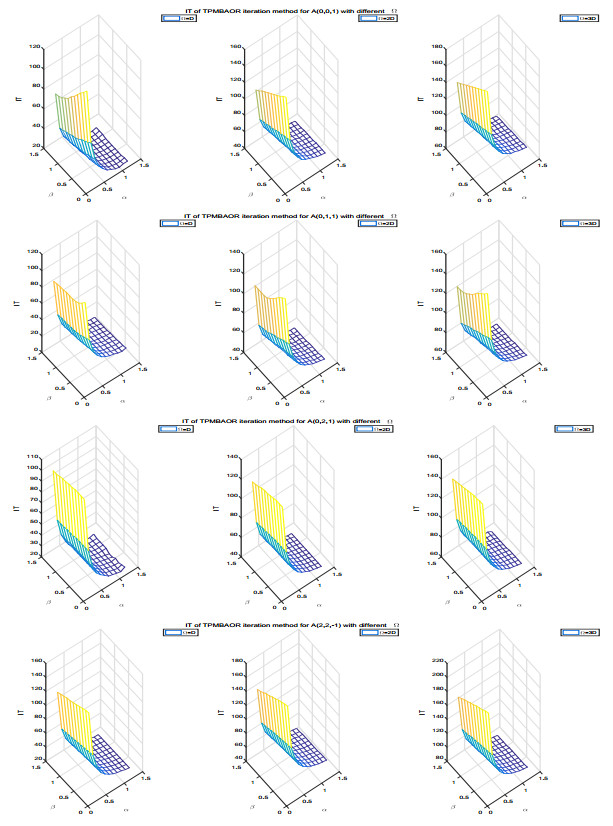
Figure 3.
The comparison of IT for the TPMBAOR iteration method with different
$ \Omega $




 DownLoad:
DownLoad: