| Citation: | Hai-Long Shen, Zhi-Min Xu, Xin-Hui Shao. THE MULTI-STEP RANDOMIZED KACZMARZ ALGORITHMS FOR SOLVING LARGE CONSISTENT LINEAR EQUATIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2522-2541. doi: 10.11948/20220414 |
THE MULTI-STEP RANDOMIZED KACZMARZ ALGORITHMS FOR SOLVING LARGE CONSISTENT LINEAR EQUATIONS
-
Abstract
In order to solve large scale consistent linear systems, based on the Kaczmarz algorithm, we propose two Multi-step Randomized Kaczmarz algorithms, denoted as MRK1 and MRK2, and give the corresponding convergence analysis. We consider using parameters to control the number of working rows. MRK1 algorithm uses a fixed parameter $ m $, and the best result is that the parameter $ m $ is the number of rows of the coefficient matrix, while MRK2 algorithm uses a randomly generated parameter $ m $, which is more general. Finally, we carry out the corresponding numerical simulation experiments, the experimental results show that, compared with the RK, GRK algorithm, the new algorithm is faster and more efficient on CPU in most cases, and the maximum CPU acceleration is 12.54. And the difference between MRK1(s), MRK2 and MGRK on CPU is not very significant according to experimental results.
-

-
References
[1] Z. Bai and W. Wu, On greedy randomized Kaczmarz method for solving large sparse linear systems, SIAM Journal on Scientific Computing, 2018, 40(1), A592–A606. doi: 10.1137/17M1137747 [2] J. Cai and Y. Tang, A new randomized Kaczmarz based kernel canonical correlation analysis algorithm with applications to information retrieval, Neural Networks, 2018, 98, 178–191. doi: 10.1016/j.neunet.2017.11.013 [3] T. A. Davis and Y. Hu, The university of Florida sparse matrix collection, ACM Transactions on Mathematical Software (TOMS), 2011, 38(1), 1–25. [4] C. Gu, M. Sun and P. F, On randomized sampling Kaczmarz method with application in compressed sensing, Mathematical Problems in Engineering, 2020, 1–11. [5] X. Jiang, Subspace algorithm and random Kaczmarz algorithm for web page sorting and their applications, PhD thesis, Shanghai University (Doctoral Dissertation), 2019. [6] S. Karczmarz, Angenaherte auflosung von systemen linearer Glei-Chungen, Bull. Int. Acad. Pol. Sic. Let., Cl. Sci. Math. Nat., 1937, 355–357. [7] C. Pechstein, M. Eslitzbichler and R. Ramlau, An H1-Kaczmarz reconstructor for atmospheric tomography, Journal of Inverse and Ill-Posed Problems, 2013, 21(3), 431–450. doi: 10.1515/jip-2013-0007 [8] C. Popa and R. Zdunek, Kaczmarz extended algorithm for tomographic image reconstruction from limited-data, Mathematics and Computers in Simulation, 2004, 65(6), 579–598. doi: 10.1016/j.matcom.2004.01.021 [9] P. Ramanan, G. Kamath and W. Song, Distributed randomized Kaczmarz and applications to seismic imaging in sensor network, In 2015 International Conference on Distributed Computing in Sensor Systems, IEEE, 2015, 169–178. [10] D. Schmidt, J. Leliaert and O. Posth, Interpreting the magnetorelaxometry signal of suspended magnetic nanoparticles with Kaczmarz'algorithm, Journal of Physics D: Applied Physics, 2017, 50(19), 195002. doi: 10.1088/1361-6463/aa695d [11] T. Strohmer and R. Vershynin, A randomized Kaczmarz algorithm with exponential convergence, Journal of Fourier Analysis and Applications, 2009, 15(2), 262. doi: 10.1007/s00041-008-9030-4 [12] J. Yin, Y. Du and K. Zhang, Greedy distance stochastic Kaczmarz method for solving large sparse linear equations, Journal of Tongji University (NATURAL SCIENCE EDITION), 2020, 48(8), 1224–1231. -
-
-
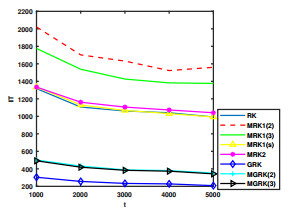
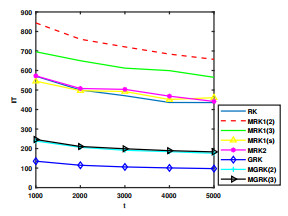
Figure 1.
IT for
$ s=50 $ $ t $ -
Figure 2.
IT for
$ s=100 $ $ t $ -
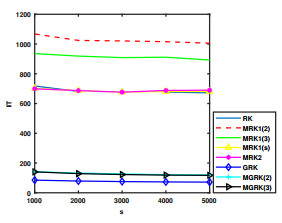
Figure 3.
IT for
$ t=50 $ $ s $ -
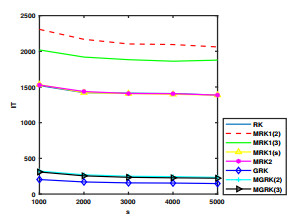
Figure 4.
IT for
$ t=100 $ $ s $ -
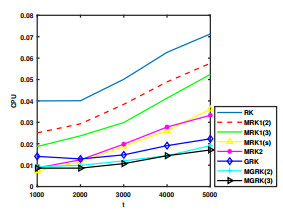
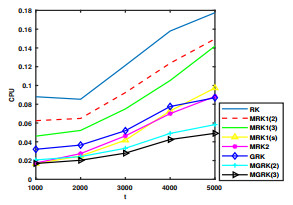
Figure 5.
CPU for
$ s=50 $ $ t $ -
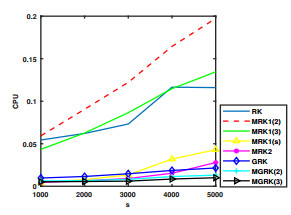
Figure 6.
CPU for
$ s=100 $ $ t $ -
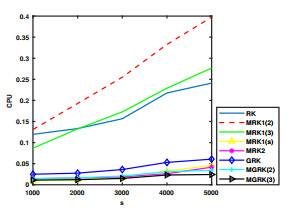
Figure 7.
CPU for
$ t=50 $ $ s $ -
Figure 8.
CPU for
$ t=100 $ $ s $




 DownLoad:
DownLoad: