| Citation: | Xiaojie He, Zhijun Liu, Qinglong Wang. PARTIAL PERMANENCE AND STATIONARY DISTRIBUTION OF A DELAYED STOCHASTIC FACULTATIVE MUTUALISM MODEL WITH FEEDBACK CONTROLS[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 657-681. doi: 10.11948/20220405 |
PARTIAL PERMANENCE AND STATIONARY DISTRIBUTION OF A DELAYED STOCHASTIC FACULTATIVE MUTUALISM MODEL WITH FEEDBACK CONTROLS
-
Abstract
This paper characterizes a facultative mutualism model with feedback controls by using delayed stochastic differential equations, in which each interspecific mutualism term contains saturation effects and distributed delays with strong kernels. Firstly, we transform the stochastic facultative mutualism model with strong kernels into an equivalent eight-dimensional stochastic model by a linear chain technique. After that, sufficient criteria for partial permanence of both species and the existence of a unique stationary distribution are established, respectively. Finally, illustrative examples and corresponding numerical simulations are carried out to support our theoretical results.
-

-
References
[1] M. A. Aizerman and F. R. Gantmacher, Absolute Stability of Regulator Systems (translated from Russian), Holden Day, San Francisco, 1964. [2] D. O. Alvarenga and K. Rousk, Unraveling host-microbe interactions and ecosystem functions in moss-bacteria symbioses, J. Exp. Bot., 2022, 73(13), 4473–4486. doi: 10.1093/jxb/erac091 [3] A. Bahar and R. X. Mao, Stochastic delay Lotka-Volterra model, J. Math. Anal. Appl., 2004, 292(2), 364–380. doi: 10.1016/j.jmaa.2003.12.004 [4] I. Barhalat, Systems d'equations differential d'oscillations nonlinearies, Rev. Roum. Math. Pures Appl., 1959, 4, 267–270. [5] A. A. Carrell, D. Veličković, T. J. Lawrence, et al., Novel metabolic interactions and environmental conditions mediate the boreal peatmoss-cyanobacteria mutualism, ISME J., 2022, 16(4), 1074–1085. doi: 10.1038/s41396-021-01136-0 [6] F. D. Chen, X. Y. Liao and Z. K. Huang, The dynamic behavior of N-species cooperation system with continuous time delays and feedback controls, Appl. Math. Comput., 2006, 181(2), 803–815. [7] F. D. Chen, J. H. Yang, L. J. Chen and X. D. Xie, On a mutualism model with feedback controls, Appl. Math. Comput., 2009, 214(2), 581–587. [8] L. J. Chen and X. D. Xie, Permanence of an N-species cooperation system with continuous time delays and feedback controls, Nonlinear Anal. Real World Appl., 2011, 12(1), 34–38. doi: 10.1016/j.nonrwa.2010.05.033 [9] Z. L. Feng, Y. D. Yang, D. S. Xu, et al., Timely identification of optimal control strategies for emerging infectious diseases, J. Theor. Biol., 2009, 259(1), 165–171. doi: 10.1016/j.jtbi.2009.03.006 [10] M. M. Gao and D. Q. Jiang, Stationary distribution of a chemostat model with distributed delay and stochastic perturbations, Appl. Math. Lett., 2022, 123, 107585. doi: 10.1016/j.aml.2021.107585 [11] K. Gopalsamy, Stability and Oscillations in Delay Differential Equations of Population Dynamics, Kluwer Academic, Dordrecht, 1992. [12] K. Gopalsamy and P. X. Weng, Feedback regulation of logistic growth, Internat. J. Math. Math. Sci., 1993, 16(1), 177–192. doi: 10.1155/S0161171293000213 [13] K. Gopalsamy and P. X. Weng, Global attractivity in a competition system with feedback controls, Comput. Math. Appl., 2003, 45(4–5), 665–676. doi: 10.1016/S0898-1221(03)00026-9 [14] R. Y. Han and F. D. Chen, Global stability of a commensal symbiosis model with feedback controls, Commun. Math. Biol. Neurosci., 2015, 2015, Article ID 15. [15] J. Hu and Z. J. Liu, Incorportating two coupling noises into a nonlinear competitive system with saturation effect, Int. J. Biomath., 2020, 13(2), 2050012. doi: 10.1142/S1793524520500126 [16] D. H. Janzen, Euglossine bees as long-distance pollinators of tropical plants, Science, 1971, 171(3967), 203–205. doi: 10.1126/science.171.3967.203 [17] C. Y. Ji and D. Q. Jiang, Persistence and non-persistence of a mutualism system with stochastic perturbation, Discrete Contin. Dyn. Syst., 2012, 32(3), 867–889. doi: 10.3934/dcds.2012.32.867 [18] C. Y. Ji, X. Yang and Y. Li, Permanence, extinction and periodicity to a stochastic competitive model with infinite distributed delays, J. Dynam. Differential Equations, 2021, 33(1), 135–176. doi: 10.1007/s10884-020-09850-7 [19] R. Z. Khas'minskii, Stochastic Stability of Differential Equations, Alphen aan den Rijn, Netherlands, 1980. [20] Y. Kuang and H. L. Smith, Global stability for in infinite delay Lotka-Volterra type system, J. Differ. Equations, 1993, 103(2), 221–246. doi: 10.1006/jdeq.1993.1048 [21] S. Lefschetz, Stability of Nonlinear Control Systems, Academic Press, New York, 1965. [22] Q. Li, Z. J. Liu and S. L. Yuan, Cross-diffusion induced turing instability for a competition model with saturation effect, Appl. Math. Comput., 2019, 347, 64–77. [23] M. Liu and K. Wang, Analysis of a stochastic autonomous mutualism model, J. Math. Anal. Appl., 2013, 402(1), 392–403. doi: 10.1016/j.jmaa.2012.11.043 [24] M. Liu, K. Wang and Q. Wu, Survival analysis of stochastic competitive models in a polluted environment and stochastic competitive exclusion principle, Bull. Math. Biol., 2011, 73(9), 1969–2012. doi: 10.1007/s11538-010-9569-5 [25] Q. Liu, D. Q. Jiang and T. Hayat, Dynamics of stochastic predator-prey models with distributed delay and stage structure for prey, Int. J. Biomath., 2021, 14(4), 2150020. doi: 10.1142/S1793524521500200 [26] Z. J. Liu, J. H. Wu, R. H. Tan and Y. P. Chen, Modeling and analysis of a periodic delayed two-species model of facultative mutualism, Appl. Math. Comput., 2010, 217(2), 893–903. [27] A. J. Lotka, Elements of Mathematical Biology, Dover, New York, 1924. [28] N. Macdonald, Time Lags in Biological Models, Lecture Notes in Biomathematics, Springer-Verlag, Berlin, 1978. [29] R. X. Mao, Stochastic Differential Equations and Applications, Horwood, Chichester, 2007. [30] R. N. Mariscal, The nature of the symbiosis between Indo-Pacific anemone fishes and sea anemones, Mar. Biol., 1970, 6(1), 58–65. doi: 10.1007/BF00352608 [31] D. Maxin, P. Georgescu, L. Sega and L. Berec, Global stability of the coexistence equilibrium for a general class of models of facultative mutualism, J. Biol. Dynam., 2017, 11(1), 339–364. doi: 10.1080/17513758.2017.1343871 [32] R. M. May, Stability and Complexity in Model Ecosystems, Princeton University Press, NJ, 2001. [33] D. Mckey, The ecology of coevolved seed dispersal systems, coevolution of animals and plants (eds. L. E. Gilbert and P. H. Raven), University of Texas Press, Austin, 1975, 159–191. [34] C. M. Moore and J. W. Dittel, On mutualism, models, and masting: The effects of seed-dispersing animals on the plants they disperse, J. Ecol., 2020, 108(5), 1775–1783. doi: 10.1111/1365-2745.13414 [35] E. P. Odum, Fundamental of Ecology, Vol. 3, Saunders, Philadelphia, 1971. [36] K. G. Poter, Enhancement of algal growth and productivity by grazing zooplankton, Science, 1967, 192(4246), 1332–1334. [37] S. H. Pryor, R. Hill, D. L. Dixson, et al., Anemonefish facilitate bleaching recovery in a host sea anemone, Sci. Rep., 2020, 10(1), 1–9. doi: 10.1038/s41598-019-56847-4 [38] K. Qi, Z. J. Liu, L. W. Wang and Q. L. Wang, Survival and stationary distribution of a stochastic facultative mutualism model with distributed delays and strong kernels, Math. Biosci. Eng., 2021, 18, 3160–3179. [39] S. G. Ruan, Delay Differential Equations in Single Species Dynamics, in Delay Differential Equations and Applications (eds. O. Arino, et al.), Springer, New York, 2006. [40] H. L. Smith, On the asymptotic behavior of a class of deterministic models of cooperating species, SIAM J. Appl. Math., 1986, 46(3), 368–375. [41] S. Y. Tang and L. S. Chen, Global qualitative analysis for a ratio-dependent predator-prey model with delay, J. Math. Anal. Appl., 2002, 266(2), 401–419. [42] C. J. Van Der Kooi, M. Vallejo-Marín and S. D. Leonhardt, Mutualisms and (a) symmetry in plant-pollinator interactions, Curr. Biol., 2021, 31(2), R91–R99. [43] V. Volterra, Lecons sur la Theorie Mathematique de la Lutte pour la Vie, Gauthier-Villars, Paris, 1931. [44] Y. N. Xiao, S. Y. Tang and J. F. Chen, Permanence and periodic solution in competitive system with feedback controls, Math. Comput. Model., 1998, 27(6), 33–37. [45] D. Y. Xu, Y. M. Huang and Z. G. Yang, Existence theorems for periodic Markov process and stochastic functional differential equations, Discrete Contin. Dyn. Syst., 2009, 24(3), 1005–1023. [46] K. Yang, H. N. Wang and F. D. Chen, On the stability property of a Lotka-Volterra cooperation system with feedback controls, Mathematica Applicata, 2014, 27(2), 243–247. (in Chinese) [47] W. J. Zuo, D. Q. Jiang, X. G. Sun, T. Hayat and A. Alsaedi, Long-time behaviors of a stochastic cooperative Lotka-Volterra system with distributed delay, Phys. A, 2018, 506, 542–559. -
-
-
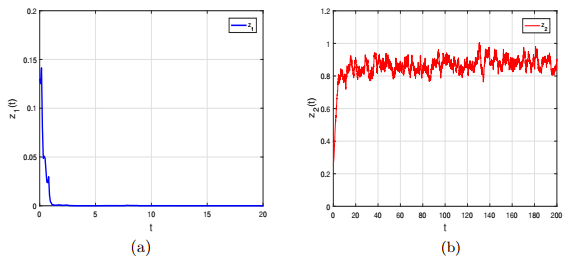
Figure 1.
(a) Permanence in time average of species
$ z_1 $ $ z_2 $ -
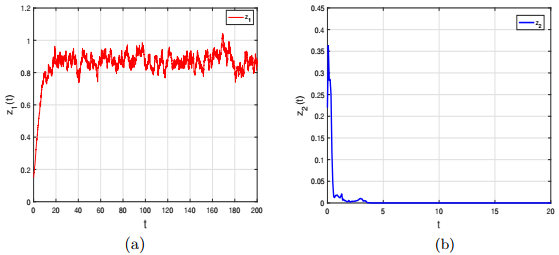
Figure 2.
(a) Exponential extinction of species
$ z_1 $ $ z_2 $ -
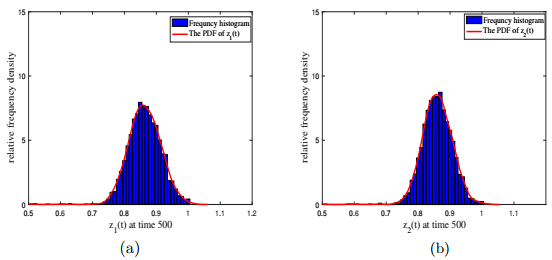
Figure 3.
(a)-(b) Frequency histograms of species
$ z_1 $ $ z_2 $ $ z_1 $ $ z_2 $ $ k_1=0.08, k_2=0.09 $ -
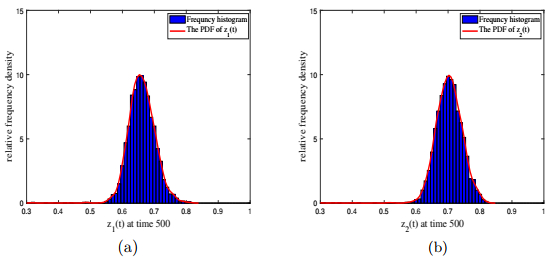
Figure 4.
(a)-(b) Frequency histograms of species
$ z_1 $ $ z_2 $ $ z_1 $ $ z_2 $ $ k_1=0.31, k_2=0.29 $




 DownLoad:
DownLoad: