| Citation: | Muhammad Nasir, Shuobing Yang, Mohammad Alqudah, Ali M. Mahnashi, Rasool Shah. APPROXIMATE SOLUTION OF FRACTIONAL-ORDER FITZHUGH-NAGUMO EQUATION WITH IN NATURAL TRANSFORM[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 624-639. doi: 10.11948/20220410 |
APPROXIMATE SOLUTION OF FRACTIONAL-ORDER FITZHUGH-NAGUMO EQUATION WITH IN NATURAL TRANSFORM
-
Abstract
In this paper, we use, for the first time, the Natural residual power series method (NRPSM) as a new iteration method to study the Caputo version of the Fitzhugh-Nagumo equation. The Fitzhugh-Nagumo equation is an essential mathematical model that is widely used to characterize the behavior of excitable systems, and is valuable for understanding significant physiological and biological processes. To start, we translate the Fitzhugh-Nagumo equation system into its Natural domain representation, and then we employ the NRPSM to obtain a series form result. After that, we present a new iteration methodology for improving the convergence characteristics of the series solution as well as the accuracy of the computations. In this paper, a comprehensive approach for investigating the Fitzhugh-Nagumo equation with Natural transform is developed and validated, thus can help researchers to explore the various dynamics and behaviors of the excitable systems more effectively. Based on the results obtained, we conclude that the suggested approach to the solution of DEs with the Caputo operator has a great potential for different applications in several fields of science and engineering.
-

-
References
[1] M. Alfaro, D. Hilhorst and H. Matano, The singular limit of the Allen-Cahn equation and the FitzHugh-Nagumo system, Journal of Differential Equations, 2008, 245(2), 505–565. doi: 10.1016/j.jde.2008.01.014 [2] A. S. Alshehry, H. Yasmin, A. Ali and I. Khan, Fractional-order view analysis of Fishers and foam drainage equations within Aboodh transform, Engineering Computations, 2024, 41(3), 489–515. doi: 10.1108/EC-08-2023-0475 [3] A. S. Alshehry, H. Yasmin, R. Ullah and A. Khan, Fractional-order modeling: Analysis of foam drainage and Fisher's equations, Open Physics, 2023, 21(1), p. 20230115. doi: 10.1515/phys-2023-0115 [4] G. A. Anastassiou, On right fractional calculus, Chaos Solit. Frac., 2009, 42(1), 365–376. doi: 10.1016/j.chaos.2008.12.013 [5] D. Baleanu, K. Diethelm, E. Scalas and J. J. Trujillo, Fractional Calculus: Models and Numerical Methods (Vol. 3), World Scientific, 2012. [6] F. B. M. Belgacem and R. Silambarasan, Theory of natural transform, aerospace (MESA), Math. Eng. Sci., 2012, 3(1), 99–124. [7] P. L. Butzer and U. Westphal, An introduction to fractional calculus, in Applications of Fractional Calculus in Physics, 2000, 1–85. [8] S. A. El-Tantawy, R. T. Matoog, R. Shah, A. W. Alrowaily and S. M. Ismaeel, On the shock wave approximation to fractional generalized Burger-Fisher equations using the residual power series transform method, Physics of Fluids, 2024, 36(2). [9] A. H. Ganie, H. Yasmin, A. A. Alderremy, R. Shah and S. Aly, An efficient semi-analytical techniques for the fractional-order system of Drinfeld-Sokolov-Wilson equation, Physica Scripta, 2024, 99(1), p. 015253. [10] M. A. Garcia-Aspeitia, G. Fernandez-Anaya, A. Hernandez-Almada, G. Leon and J. Magana, Cosmology under the fractional calculus approach, Monthly Notices of the Royal Astronomical Society, 2022, 517(4), 4813–4826. doi: 10.1093/mnras/stac3006 [11] M. M. A. Hammad, A. W. Alrowaily, S. M. Ismaeel and S. A. El-Tantawy, Analytical analysis of fractional nonlinear Jaulent-Miodek system with energy-dependent Schrodinger potential, Frontiers in Physics, 2023, 11, p. 1148306. doi: 10.3389/fphy.2023.1148306 [12] R. Hilfer (ed), Application of Fractional Calculus in Physics, World Scientific Publishing Co., Singapore, 2000. [13] B. Inan, K. K. Ali, A. Saha and T. Ak, Analytical and numerical solutions of the Fitzhugh-Nagumo equation and their multistability behavior, Numerical Methods for Partial Differential Equations, 2021, 37(1), 7–23. doi: 10.1002/num.22516 [14] Z. H. Khan and W. A. Khan, N-transform properties and applications, NUST J. Eng. Sci., 2008, 1(1), 127–133. [15] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, 24, North-Holland Mathematics Studies, Amsterdame, 2006. [16] M. Krupa, B. Sandstede and P. Szmolyan, Fast and slow waves in the FitzHugh-Nagumo equation, Journal of Differential Equations, 1997, 133(1), 49–97. doi: 10.1006/jdeq.1996.3198 [17] D. Kumar, J. Singh and D. Baleanu, A new numerical algorithm for fractional Fitzhugh-Nagumo equation arising in transmission of nerve impulses, Nonlinear Dynamics, 2018, 91, 307–317. doi: 10.1007/s11071-017-3870-x [18] S. Kumar, A. Yildirim, Y. Khan and L. Wei, A fractional model of the diffusion equation and its analytical solution using Laplace transform, Sci. Iran. B, 2012, 19(4), 1117–1123. doi: 10.1016/j.scient.2012.06.016 [19] J. E. Macias-Diaz, A. S. Hendy and N. S. Markov, A bounded numerical solver for a fractional FitzHugh-Nagumo equation and its high-performance implementation, Engineering with Computers, 2021, 37, 1593–1609. doi: 10.1007/s00366-019-00902-1 [20] I. Y. Miranda-Valdez, J. G. Puente-Cordova, F. Y. Renteria-Baltierrez, L. Fliri, M. Hummel, A. Puisto, J. Koivisto and M. J. Alava, Viscoelastic phenomena in methylcellulose aqueous systems: Application of fractional calculus, Food Hydrocolloids, 2024, 147, p. 109334. doi: 10.1016/j.foodhyd.2023.109334 [21] S. Noor, W. Albalawi, R. Shah, M. M. Al-Sawalha and S. M. Ismaeel, Mathematical frameworks for investigating fractional nonlinear coupled Korteweg-de Vries and Burgers equations, Frontiers in Physics, 2024, 12, p. 1374452. doi: 10.3389/fphy.2024.1374452 [22] S. Noor, A. S. Alshehry and A. Shafee, Families of propagating soliton solutions for (3+ 1)-fractional Wazwaz-Benjamin Bona-Mahony equation through a novel modification of modified extended direct algebraic method, Physica Scripta, 2024, 99(4), p. 045230. [23] H. S. Patel and T. Patel, Applications of fractional reduced differential transform method for solving the generalized fractional-order Fitzhugh-Nagumo equation, International Journal of Applied and Computational Mathematics, 2021, 7(5), p. 188. doi: 10.1007/s40819-021-01130-2 [24] P. Ramani, A. M. Khan, D. L. Suthar and D. Kumar, Approximate analytical solution for non-linear Fitzhugh-Nagumo equation of time fractional order through fractional reduced differential transform method, International Journal of Applied and Computational Mathematics, 2022, 8(2), p. 61. doi: 10.1007/s40819-022-01254-z [25] K. Shah, H. Khalil and R. A. Khan, Analytical solutions of fractional order diffusion equations by natural transform method, Iranian Journal of Science and Technology, Transactions A: Science, 2018, 42(3), 1479–1490. doi: 10.1007/s40995-016-0136-2 [26] R. Silambarasn and F. B. M. Belgacem, Applications of the natural trans-form to Maxwell's equations, progress, in: Electromagnet ics research symposium proceedings, Suzhou, China, Sept., 2011, 12(16), 11 pp. [27] E. Yanagida, Stability of fast travelling pulse solutions of the FitzHugh-Nagumo equations, Journal of Mathematical Biology, 1985, 22, 81–104. [28] Q. Yang, D. Chen, T. Zhao and Y. Chen, Fractional calculus in image processing: A review, Fractional Calculus and Applied Analysis, 2016, 19(5), 1222–1249. doi: 10.1515/fca-2016-0063 [29] A. Yokus, On the exact and numerical solutions to the FitzHugh-Nagumo equation, International Journal of Modern Physics B, 2020, 34(17), p. 2050149. doi: 10.1142/S0217979220501490 -
-
-
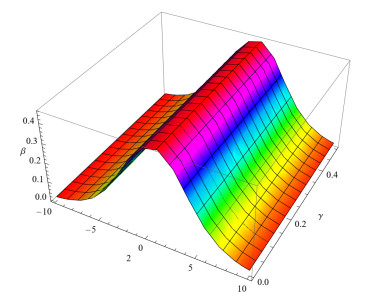
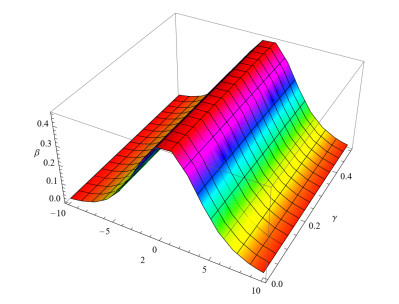
Figure 1.
The fractional order
$ p=1.0 $ -
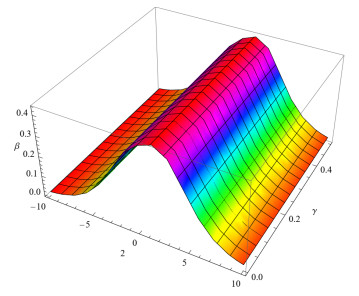
Figure 2.
The fractional order
$ p=0.8 $ -
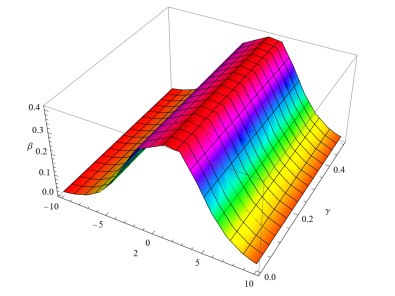
Figure 3.
The fractional order
$ p=0.6 $ -
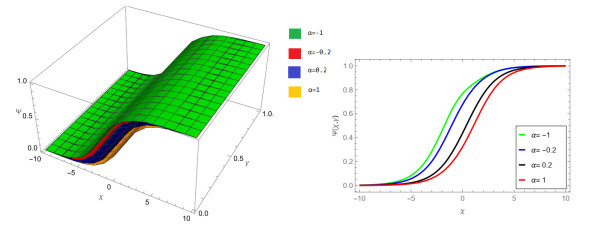
Figure 4.
The fractional order
$ p=0.4 $ -
Figure 5.
NITM result of Example 1 for fractional-order
$ p=1 $




 DownLoad:
DownLoad: