| Citation: | Qianhong Zhang, Fei Jin, Zhongni Zhang, Bairong Pan. ASYMPTOTIC FEATURE OF DISCRETE SECOND-ORDER FUZZY DIFFERENCE EQUATION WITH QUADRATIC TERM[J]. Journal of Applied Analysis & Computation, 2025, 15(2): 640-656. doi: 10.11948/20230342 |
ASYMPTOTIC FEATURE OF DISCRETE SECOND-ORDER FUZZY DIFFERENCE EQUATION WITH QUADRATIC TERM
-
Abstract
This article explores the asymptotic feature of a discrete second-order fractal FDE (fuzzy difference equation) with quadratic term. Specifically, applying a generalization of division (g-division) of two fuzzy numbers, we obtain dynamical features including the boundedness, persistence, and global behavior of a positive fuzzy solution of the following model
$ x_{n+1}=A+\frac{Bx_{n}^2}{x_{n-1}^2}, \ \ n\in N^+, $
where the parameters $A, B\in \Re_f^+$(positive fuzzy number) and the initial values $x_0, x_{-1}\in \Re_f^+$. Finally, two numerical examples are provided to reveal the validity of our findings.
-
Keywords:
- g-division /
- fractal FDE /
- persistence /
- boundedness /
- global asymptotic feature
-

-
References
[1] R. M. Abu-Saris and R. DeVault, Global stability of $y_{n+1}=A+\frac {y_n}{y_{n-k}}$, Appl. Math. Lett., 2003, 16, 173–178. doi: 10.1016/S0893-9659(03)80028-9 CrossRef $y_{n+1}=A+\frac {y_n}{y_{n-k}}$" target="_blank">Google Scholar
[2] R. P. Agarwal, W. T. Li and P. Y. H. Pang, Asymptotic behavior of a class of nolinear delay difference equations, J. Differ. Equat. Appl., 2002, 8, 719–728. doi: 10.1080/1023619021000000735 [3] L. Berg and S. Stevic, On some systems of difference equations, Appllied Mathematics and Computation, 2011, 218, 1713–1718. doi: 10.1016/j.amc.2011.06.050 [4] E. Beso, S. Kalabusic, N. Mujic and E. Pilav, Boundedness of solutions and stability of certain second-order difference equation with quadratic term, Advances in Difference Equations, 2020, 19, 1–22. [5] M. Bohner and S. Streipert, Optimal harvesting policy for the Beverton-Holt model, Mathematical Biosciences and Engineering, 2016, 13, 673–695. doi: 10.3934/mbe.2016014 [6] K. A. Chrysafis, B. K. Papadopoulos and G. Papaschinopoulos, On the fuzzy difference equations of finance, Fuzzy Sets and Systems, 2008, 159(24), 3259–3270. doi: 10.1016/j.fss.2008.06.007 [7] E. Y. Deeba and A. De Korvin, Analysis by fuzzy difference equations of a model of $CO_2$ level in the blood, Appl. Math. Lett., 1999, 12, 33–40. doi: 10.1016/S0893-9659(98)00168-2 CrossRef $CO_2$ level in the blood" target="_blank">Google Scholar
[8] E. Y. Deeba, A. De Korvin and E. L. Koh, A fuzzy difference equation with an application, J. Difference Equation Appl., 1996, 2, 365–374. doi: 10.1080/10236199608808071 [9] L. Gutnik and S. Stevic, On the behaviour of the solutions of a second order difference equation, Discrete Dyn. Nat. Soc., 2007, article ID 27562. [10] M. Hua, P. Cheng, J. Fei, J. Zhang and J. Chen, Robust H1-Ltering for uncertain discrete-time fuzzy stochastic systems with sensor nonlinearities and time-varying delay, Journal of Applied Mathematics, 2012, article ID 402480, 25 pp. [11] T. F. Ibrahim and Q. Zhang, Stability of an anti-competitive system of rational difference equations, Archives Des Sciences, 2013, 66(5), 44–58. [12] K. Ivaz, A. Khastan and J. J. Nieto, A numerical method of fuzzy differential equations and hybrid fuzzy differential equations, Abstract and Applied Analysis, 2013, article ID 735128, 10 pp. [13] A. Khastan, Fuzzy logistic difference equation, Iran. J. Fuzzy Syst., 2018, 15, 55–66. [14] T. Khyat, M. R. S. Kulenovic and E. Pilav, The Naimarck-Sacker bifurcation of a certain difference equation, Journal of Computational Analysis and Applications, 2017, 23(8), 1335–1346. [15] C. Kocak, First-order ARMA type fuzzy time series method based on fuzzy logic relation tables, Mathematical Problems in Engineering, 2013, article ID 769125, 12 pp. [16] V. L. Kocic and G. Ladas, Global Behavior of Nonlinear Difference Equations of Higher Order with Application, Kluwer Academic Publishers, Dordrecht, 1993. [17] M. R. S. Kulenonvic and G. Ladas, Dynamics of Second Order Rational Difference Equations with Open Problems and Conjectures, Chapaman & Hall/CRC, Boca Raton, 2002. [18] V. Lakshmikantham and A. S. Vatsala, Basic theory of fuzzy difference equations, J. Differ. Equ. Appl., 2002, 8(11), 957–968. doi: 10.1080/1023619021000048850 [19] W. Liu, D. Cai and J. Shi, Dynamic behaviors of a discrete-time predator-prey bioeconomic system, Adv. Differ. Equ., 2018, 2018, 133. doi: 10.1186/s13662-018-1592-0 [20] M. T. Malinowski, On a new set-valued stochastic integral with respect to semi-martingales and its applications, Journal of Mathematical Analysis and Applications, 2013, 408, 669–680. doi: 10.1016/j.jmaa.2013.06.054 [21] M. T. Malinowski, Some properties of strong solutions to stochastic fuzzy differential equations, Information Sciences, 2013, 252, 62–80. doi: 10.1016/j.ins.2013.02.053 [22] M. T. Malinowski, Approximation schemes for fuzzy stochastic integral equations, Applied Mathematics and Computation, 2013, 219, 11278–11290. doi: 10.1016/j.amc.2013.05.040 [23] S. P. Mondal, D. K. Vishwakarma and A. K. Saha, Solution of second order linear fuzzy difference equation by Lagrange's multiplier method, J. Soft Comput. Appl., 2016, 1, 11–27. [24] C. Mylona, G. Papaschinopoulos and C. J. Schinas, Stability and flip bifurcation of a three-dimensional exponential system of difference equations, Math. Methods Appl. Sci., 2021, 44(6), 4316–4329. doi: 10.1002/mma.7031 [25] M. Ouyang, Q. Zhang, M. Cai and Z. Zeng, Dynamic analysis of a fuzzy Bobwhite quail population model under g-division law, Scientific Report, 2024, 14, 9682. doi: 10.1038/s41598-024-60178-4 [26] M. Ouyang, Q. Zhang and Z. Chen, Balanced harvesting of dynamical discrete Ricker and Beverton-Holt system, Chaos, Solitons and Fractals, 2023, 170, 113384. doi: 10.1016/j.chaos.2023.113384 [27] G. Papaschinopoulos and B. K. Papadopoulos, On the fuzzy difference equation $x_{n+1}=A+B/x_n$, Soft Comput., 2002, 6, 456–461. doi: 10.1007/s00500-001-0161-7 [28] G. Papaschinopoulos and B. K. Papadopoulos, On the fuzzy difference equation $x_{n+1}=A+x_n/x_{n-m}$, Fuzzy Sets and Systems, 2002, 129, 73–81. doi: 10.1016/S0165-0114(01)00198-1 CrossRef $x_{n+1}=A+x_n/x_{n-m}$" target="_blank">Google Scholar
[29] G. Papaschinopoulos and C. J. Schinas, On the fuzzy difference equation $x_{n+1}=\sum_{i=0}.{k-1}A_i/x_{n-i}.p_i+1/x_{n-k}.p_k$, J. Difference Equation Appl., 2002, 6, 75–89. $x_{n+1}=\sum_{i=0}.{k-1}A_i/x_{n-i}.p_i+1/x_{n-k}.p_k$" target="_blank">Google Scholar
[30] G. Papaschinopoulos and C. J. Schinas, On a system of two nonlinear difference equations, J. Math. Anal. Appl., 1998, 219, 415–426. [31] G. Papaschinopoulos and G. Stefanidou, Boundedness and asymptotic behavior of the solutions of a fuzzy difference equation, Fuzzy Sets and Systems, 2003, 140, 523–539. [32] M. Parsamanesh and S. Mehrshad, Stability of the equilibria in a discrete-time SIVS epidemic model with standard incidence, Filomat, 2019, 33(8), 2393–2408. [33] G. Stefanidou and G. Papaschinopoulos, A fuzzy difference equation of a rational form, J. Nonlin. Math. Phys., 2005, 12(2), 300–315. [34] G. Stefanidou, G. Papaschinopoulos and C. J. Schinas, On an exponential-type fuzzy difference equation, Advances in Difference Equations, 2010. DOI: 10.1155/2010/196920. [35] L. Stefanini, A generalization of Hukuhara difference and division for interval and fuzzy arithmetic, Fuzzy Sets and Systems, 2010, 161, 1564–1584. [36] T. Sun, G. Su and B. Qin, On the fuzzy difference equation $x_n=F(x_{n-1}, x_{n-k})$, Fuzzy Sets and Systems, 2020, 387, 81–88. [37] C. Wang and J. Li, Periodic solution for a max-type fuzzy difference equation, Journal of Mathematics, 2020, 3, 1–12. [38] C. Wang, X. Su, P. Liu, X. Hu and R. Li, On the dynamics of a five-order fuzzy difference equation, Journal of Nonlinear Science and Applications, 2017, 10, 3303–3319. [39] L. Xiang, Y. Zhang and J. Huang, Stability analysis of a discrete SIRS epidemic model with vaccination, J. Difer. Equ. Appl., 2020, 26(3), 309–327. [40] I. Yalcnkaya, H. El-Metwally, D. T. Tollu and H. Ahmad, Behavior of solutions to the fuzzy difference equation, Mathematical Notes, 2023, 113(1–2), 292–302. [41] X. Yang, On the system of rational difference equations $x_n=A+y_{n-1}/x_{n-p}y_{n-q}, y_n=A+x_{n-1}/x_{n-r}y_{n-s}$, J. Math. Anal. Appl., 2005, 307, 305–311. $x_n=A+y_{n-1}/x_{n-p}y_{n-q}, y_n=A+x_{n-1}/x_{n-r}y_{n-s}$" target="_blank">Google Scholar
[42] Q. Zhang, J. Liu and Z. Luo, Dynamical behavior of a third-order rational fuzzy difference equation, Advances in Difference Equations, 2015, 108. DOI: 10.1186/s13662-015-0438-2. [43] Q. Zhang, M. Ouyang, B. Pan and F. Lin, Qualitative analysis of second-order fuzzy difference equation with quadratic term, Journal of Applied Mathematics and Computing, 2023, 69, 1355–1376. [44] Q. Zhang, B. Pan, M. Ouyang and F. Lin, Large time behavior of solution to second-order fractal difference equation with positive fuzzy parameters, Journal of Intelligent and Fuzzy Systems, 2023, 45, 5709–5721. [45] Q. Zhang, L. Yang and D. Liao, Behavior of solutions to a fuzzy nonlinear difference equation, Iranian Journal of Fuzzy Systems, 2012, 9, 1–12. [46] Q. Zhang, L. Yang and D. Liao, On first order fuzzy Ricatti difference equation, Inform. Sci., 2014, 270, 226–236. [47] Q. Zhang, L. Yang and J. Liu, Dynamics of a system of rational third-order difference equation, Advances in Difference Equations, 2012, 2012(136), 1–8. [48] Q. Zhang, W. Zhang, F. Lin and D. Li, On dynamic behavior of second-order exponential-type fuzzy difference equation, Fuzzy Sets and Systems, 2021, 419, 169–187. -
-
-
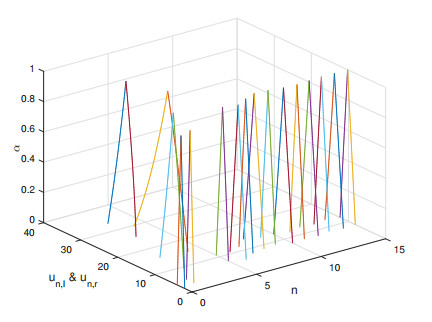
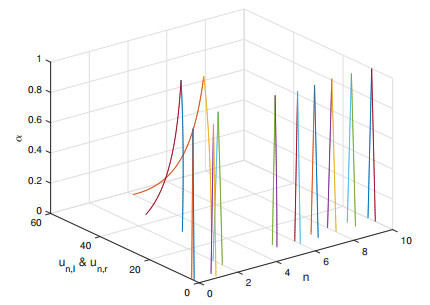
Figure 1.
The Dynamics of system (4.7).
-
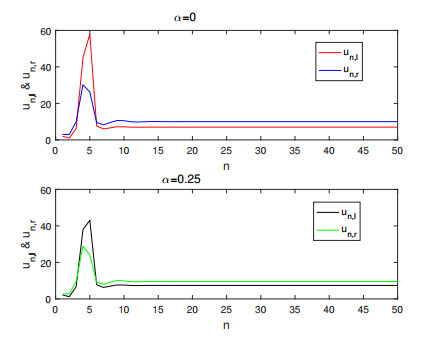
Figure 2.
The solution of system (4.7) at
$ \alpha=0 $ $ \alpha=0.25 $ -
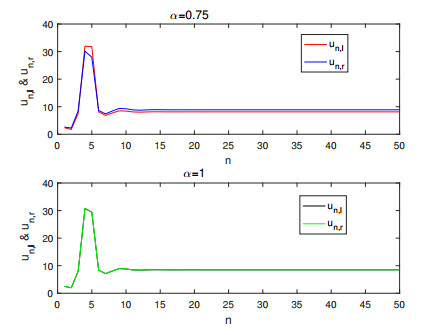
Figure 3.
The solution of system (4.7) at
$ \alpha=0.75 $ $ \alpha=1 $ -
Figure 4.
The Dynamics of system (4.13).
-
Figure 5.
The solution of system (4.13) at
$ \alpha=0 $ $ \alpha=0.25 $ -
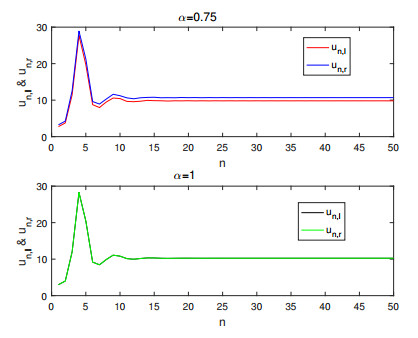
Figure 6.
The solution of system (4.13) at
$ \alpha=0.75 $ $ \alpha=1 $




 DownLoad:
DownLoad: