| Citation: |
Ji Li, Ping Li. THE EFFECT OF AN ADDITIVE NOISE ON SOME SLOW-FAST EQUATION NEAR A TRANSCRITICAL POINT[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1632-1649. doi: 10.11948/20220433
|
THE EFFECT OF AN ADDITIVE NOISE ON SOME SLOW-FAST EQUATION NEAR A TRANSCRITICAL POINT
-
Abstract
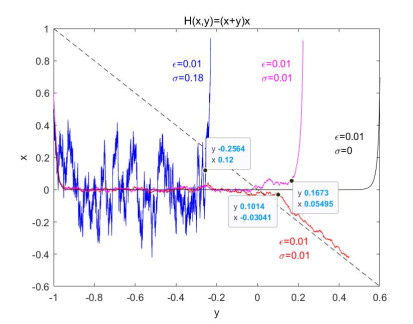
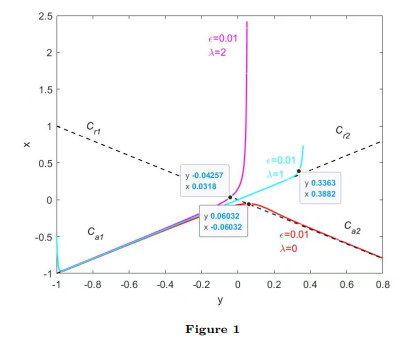
We consider the effect of small additive noise with intensity $ \sigma $ on trajectories of a slow-fast system with small parameter $ \varepsilon $ which admits bifurcation delay at a transcritical point. We estimate the probability that the perturbed stochastic paths stay in some tubular neighborhood of the deterministic path to show that small but not exponentially small noise destroys the bifurcation delay caused by transcritical point and obtain a noise intensity threshold value $ N(\varepsilon) $ of order $ \varepsilon^{\frac{3}{4}} $. When $ e^{-\frac{1}{\varepsilon}}\ll\sigma<N(\varepsilon) $, the paths are likely to leave the neighborhood of the corresponding determinate path before some time of order $ \sqrt{\varepsilon|log\sigma|} $. When $ \sigma>N(\varepsilon) $, the paths are likely to leave before some time of order $ \sigma^{\frac{2}{3}} $.
-
-
References
[1] E. Benoît, Equations différentielles:rélation entree-sortie, Comptes Rendus des Séances de l'Académie des Sciences. Série I. Mathématique, 1981,293(5), 293–296. [2] E. Benoît, Dynamic Bifurcations(Luminy, 1990), Springer, Berlin, 1991. [3] N. Berglund and B. Gentz, Pathwise description of dynamic pitchfork bifurcations with additive noise, Probability Theory and Related Fields, 2002,122(3), 341–388. doi: 10.1007/s004400100174 [4] N. Berglund and B. Gentz, Noise-induced phenomena in slow-fast dynamical systems, Springer-Verlag London, London, 2006. [5] H. Boudjellaba and T. Sari, Dynamic transcritical bifurcations in a class of slow-fast predator-prey models, Journal of Differential Equations, 2009,246(6), 2205–2225. doi: 10.1016/j.jde.2009.01.001 [6] H. Crauel and F. Flandoli, Attractors for random dynamical systems, Probability Theory and Related Fields, 1994,100(3), 365–393. doi: 10.1007/BF01193705 [7] A. Dembo and O. Zeitouni, Large Deviation Techniques and Applications. Second edition, Springer-Verlag, Berlin, 2010. [8] M. Diener, The canard unchained or how fast/slow dynamical systems bifurcate, The Mathematical Intelligencer, 1984, 6(3), 38–49. doi: 10.1007/BF03024127 [9] J. Eilertsen, M. A. Tyczynska and S. Schnell, Hunting $\varepsilon$:The origin and validity of quasi-steady-state reductions in enzyme kinetics, SIAM Journal on Applied Dynamical Systems, 2021, 20(4), 2450–2481. doi: 10.1137/20M135073X [10] M. Engel and H. Jardón-Kojakhmetov, Extended and symmetric loss of stability for canards in planar fast-slow maps, SIAM Journal on Applied Dynamical Systems, 2020, 19(4), 2530–2566. doi: 10.1137/20M1313611 [11] M. Engel and C. Kuehn, Discretized fast-slow systems near transcritical singularities, Nonlinearity, 2019, 32(7), 2365–2391. doi: 10.1088/1361-6544/ab15c1 [12] N. Fenichel, Persistence and smoothness of invariant manifolds for flows, Indiana University Mathematics Journal, 1971, 21(3), 193–226. doi: 10.1512/iumj.1972.21.21017 [13] N. Fenichel, Geometric singular perturbation theory for ordinary differential equations, Journal of Differential Equations, 1979, 31(1), 53–98. doi: 10.1016/0022-0396(79)90152-9 [14] M. I. Freidlin and A. D. Wentzell, Random Perturbations of Dynamical Systems. Third edition, Springer, Heidelberg, 2012. [15] X. Han and H. N. Najm, Dynamical structures in stochastic chemical reaction systems, SIAM Journal on Applied Dynamical Systems, 2014, 13(3), 1328–1351. doi: 10.1137/140957482 [16] T. H. Hsu, On bifurcation delay:An alternative approach using geometric singular perturbation theory, Journal of Differential Equations, 2017,262(3), 1617–1630. doi: 10.1016/j.jde.2016.10.022 [17] T. Hurth and C. Kuehn, Random switching near bifurcations, Stochastics and Dynamics, 2020, 20(02), 2050008, 28 pp. [18] H. Jardón-Kojakhmetov, C. Kuehn, A. Pugliese and M. Sensi, A geometric analysis of the SIR, SIRS and SIRWS epidemiological models, Nonlinear Analysis:Real World Applications, 2021, 58, 103220, 27 pp. doi: 10.1016/j.nonrwa.2020.103220 [19] M. Krupa and P. Szmolyan, Extending slow manifolds near transcritical and pitchfork singularities, Nonlinearity, 2001, 14(6), 1473–1491. doi: 10.1088/0951-7715/14/6/304 [20] C. Kuehn, A mathematical framework for critical transitions: bifurcations, fast-slow systems and stochastic dynamics, Physica D: Nonlinear Phenomena, 2011,240(12), 1020–1035. doi: 10.1016/j.physd.2011.02.012 [21] C. Kuehn, A mathematical framework for critical transitions:normal forms, variance and applications, Journal of Nonlinear Science, 2013, 23(3), 457–510. doi: 10.1007/s00332-012-9158-x [22] C. Kuehn, Normal hyperbolicity and unbounded critical manifolds, Nonlinearity, 2014, 27(6), 1351–1366. doi: 10.1088/0951-7715/27/6/1351 [23] C. Kuehn, Multiple Time Scale Dynamics, Springer, Cham., 2015. [24] C. Kuehn, N. Berglund, C. Bick, et~al., A general view on double limits in differential equations, Physica D:Nonlinear Phenomena, 2022,431, 133105, 26 pp. [25] R. Kuske, Probability densities for noisy delay bifurcations, Journal of Statistical Physics, 1999, 96(3–4), 797–816. [26] J. Li, K. Lu and P. W. Bates, Invariant foliations for random dynamical systems, Discrete and Continuous Dynamical Systems, 2014, 34(9), 3639–3666. doi: 10.3934/dcds.2014.34.3639 [27] J. Li, K. Lu and P. W. Bates, Geometric singular perturbation theory with real noise, Journal of Differential Equations, 2015,259(10), 5137–5167. doi: 10.1016/j.jde.2015.06.023 [28] W. Liu, Exchange lemmas for singular perturbation problems with certain turning points, Journal of Differential Equations, 2000,167(1), 134–180. doi: 10.1006/jdeq.2000.3778 [29] H. Lu, M. Ni and L. Wu, Extending slow manifold near generic transcritical canard point, Acta Mathematicae Applicatae Sinica, English Series, 2017, 33(4), 989–1000. doi: 10.1007/s10255-017-0713-y [30] P. D. Maesschalck and S. Schecter, The entry-exit function and geometric singular perturbation theory, Journal of Differential Equations, 2016,260(8), 6697–6715. doi: 10.1016/j.jde.2016.01.008 [31] E. F. Mishchenko, Y. S. Kolesov, A. Y. Kolesov and N. K. Rozov, Asymptotic methods in singularly perturbed systems, Consultants Bureau, New York, 1994. [32] S. M. O'Regan and J. M. Drake, Theory of early warning signals of disease emergenceand leading indicators of elimination, Theoretical Ecology, 2013, 6(3), 333–357. doi: 10.1007/s12080-013-0185-5 [33] S. Schecter, Exchange lemmas. 1. deng's lemma, Journal of Differential Equations, 2008,245(2), 392–410. doi: 10.1016/j.jde.2007.08.011 [34] M. Scheffer, J. Bascompte, W. Brock, et~al., Early-warning signals for critical transitions, Nature, 2009,461(7260), 53–59. doi: 10.1038/nature08227 [35] A. Vidal and J. P. Françoise, Canard cycles in global dynamics, International Journal of Bifurcation and Chaos, 2012, 22(2), 1250026, 13. [36] C. Wang and X. Zhang, Stability loss delay and smoothness of the return map in slow-fast systems, SIAM Journalon Applied Dynamical Systems, 2018, 17(1), 788–822. doi: 10.1137/17M1130010 [37] A. Widder and C. Kuehn, Heterogeneous population dynamics and scaling laws near epidemic outbreaks, Mathematical Biosciences and Engineering, 2016, 13(5), 1093–1118. doi: 10.3934/mbe.2016032 [38] L. Zhong and J. Shen, Degenerate transcritical bifurcation point can be an attractor:A case study in a slow-fast modified Leslie-Gower model, Qualitative Theory of Dynamical Systems, 2022, 21(3), 76, 11 pp. -
-
Figures(2)
Export File
Citation
Ji Li, Ping Li. THE EFFECT OF AN ADDITIVE NOISE ON SOME SLOW-FAST EQUATION NEAR A TRANSCRITICAL POINT[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1632-1649. doi: 10.11948/20220433
Format
Content
DownLoad:
-
Figure 1.
-
Figure 2.