| Citation: |
Lili Jia, Zongxin Lei, Changyou Wang, Yuqian Zhou, Tao Jiang, Yuanhua Du, Qiuyan Zhang. PROJECTION SYNCHRONIZATION OF FUNCTIONAL FRACTIONAL-ORDER NEURAL NETWORKS WITH VARIABLE COEFFICIENTS[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 1070-1087. doi: 10.11948/20220491
|
PROJECTION SYNCHRONIZATION OF FUNCTIONAL FRACTIONAL-ORDER NEURAL NETWORKS WITH VARIABLE COEFFICIENTS
-
Abstract
In this paper, the projection synchronization problem of functional fractional-order neural networks with variable coefficients and Caputo derivatives is studied. Firstly, a simple global projection synchronization scheme is designed according to the open-loop and adaptive feedback control. Secondly, by constructing a suitable Lyapunov function and utilizing the properties of delayed fractional-order differential inequalities, some criteria for the global projective synchronization of the variable coefficient functional neural networks with Caputo derivatives are obtained. Finally, a numerical example with many numerical simulations is employed to demonstrate the correctness and validity of the proposed method in this paper.
-
-
References
[1] H. Bao and J. Cao, Projective synchronization of fractional-order memristor-based neural networks, Neural Networks, 2015, 63, 1–9. doi: 10.1016/j.neunet.2014.10.007 [2] S. Baluni, V. K. Yadav and S. Das, Quasi projective synchronization of time varying delayed complex valued Cohen-Grossberg neural networks, Information Sciences, 2022, 612, 231–240. doi: 10.1016/j.ins.2022.08.106 [3] B. Chen and J. Chen, Razumikhin-type stability theorems for functional fractional-order differential systems and applications, Applied Mathematics and Computation, 2015, 254, 63–69. doi: 10.1016/j.amc.2014.12.010 [4] C. Chen and Z. Ding, Projective synchronization of nonidentical fractional-Order memristive neural networks, Discrete Dynamics in Nature and Society, 2019, 2019. Article ID: 8743482. [5] J. Chen, C. Lin, et al., Mixed ${{H}_{\infty}}$ and passive control for singular systems with time delay via static output feedback, Applied Mathematics and Computation, 2017, 293, 244–253. doi: 10.1016/j.amc.2016.08.029 CrossRef ${{H}_{\infty}}$ and passive control for singular systems with time delay via static output feedback" target="_blank">Google Scholar
[6] J. Chen, L. Jiao, et al., Projective synchronization with different scale factors in a driven-response complex network and its application in image encryption, Nonlinear Analysis-Real World Applications, 2010, 11, 3045–3058. doi: 10.1016/j.nonrwa.2009.11.003 [7] X. Du, H. Zhao and X. Chang, Unknown input observer design for fuzzy systems with uncertainties, Applied Mathematics and Computation, 2015, 266, 108–118. doi: 10.1016/j.amc.2015.05.046 [8] W. Guo, Lag synchronization of complex networks via pinning control, Nonlinear Analysis-Real World Applications, 2011, 12, 2579–2585. doi: 10.1016/j.nonrwa.2011.03.007 [9] Y. Gu, Y. Yu and H. Wang, Projective synchronization for fractional-order memristor-based neural networks with time delays, Neural Computing and Applications, 2019, 31, 6039–6054. doi: 10.1007/s00521-018-3391-7 [10] R. Guo, W. Lv and Z. Zhang, Quasi-projective synchronization of stochastic complex-valued neural networks with time-varying delay and mismatched parameters, Neurocomputing, 2020, 415, 184–192. doi: 10.1016/j.neucom.2020.07.033 [11] M. Hu, Y. Yang and Z. Xu, Impulsive control of projective synchronization in chaotic systems, Physics Letters A, 2008, 372, 3228–3233. doi: 10.1016/j.physleta.2008.01.054 [12] M. Hu, Z. Xu and Y. Yang, Projective cluster synchronization in drive-response dynamical networks, Physica A: Statistical Mechanics and its Applications, 2008, 387, 3759–3768. doi: 10.1016/j.physa.2008.02.066 [13] A. Hu, J. Cao, et al., Cluster synchronization in directed networks of non-identical systems with noises via random pinning control, Physica A: Statistical Mechanics and Its Applications, 2014, 395, 537–548. doi: 10.1016/j.physa.2013.10.040 [14] Y. Huang, S. Chen, et al., Coexistence and local Mittag-Leffler stability of fractional-order recurrent neural networks with discontinuous activation functions, Chinese Physics B, 2019, 28. Article ID: 040701. [15] J. He, F. Chen, et al., Global adaptive matrix-projective synchronization of delayed fractional-order competitive neural network with different time scales, Neural Computing and Applications, 2020, 32, 12813–2826. doi: 10.1007/s00521-020-04728-7 [16] W. Huang, Q. Song and Z. Zhao, Robust stability for a class of fractional-order complexvalued projective neural networks with neutral-type delays and uncertain parameters, Neurocomputing, 2021, 450, 399–410. doi: 10.1016/j.neucom.2021.04.046 [17] T. Jiang, Q. Zhang, et al., Multi-type object tracking based on residual neural network model, Symmetry, 2022, 14. Article ID: 1689. [18] J. Luo, W. Tian, et al., Non-fragile asynchronous ${{H}_{\infty}}$ control for uncertain stochastic memory systems with Bernoulli distribution, Applied Mathematics and Computation, 2017, 312, 109–128. doi: 10.1016/j.amc.2017.05.003 CrossRef ${{H}_{\infty}}$ control for uncertain stochastic memory systems with Bernoulli distribution" target="_blank">Google Scholar
[19] M. Li, X. Yang, et al., Robust asymptotic stability and projective synchronization of time-varying delayed fractional neural networks under parametric uncertainty, Neural Processing Letters, 2022. https://doi.org/10.1007/s11063-022-10825-6. doi: 10.1007/s11063-022-10825-6 [20] P. Liu, M. Kong and Z. Zeng, Projective synchronization analysis of fractional-order neural networks with mixed time delays, IEEE Transactions on Cybernetics, 2022, 52, 6798–6808. doi: 10.1109/TCYB.2020.3027755 [21] B. B. Mandelbrot, How long is the coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science, 1967, 156(3775), 636–638. doi: 10.1126/science.156.3775.636 [22] B. B. Mandelbrot, The Fractal Geometry of Nature, New York: W. H. Freeman and Company, 1982. [23] L. Pan, W. Zhou, et al., Synchronization and anti-synchronization of new uncertain fractional-order modified unified chaotic systems, Communications in Nonlinear Science and Numerical Simulation, 2010, 15, 3754–3762 doi: 10.1016/j.cnsns.2010.01.025 [24] I. Podlubny, Fractional differential equations, San Diego: Academic Press, 1999. [25] S. Qureshi and S. Aziz, Fractional modeling for a chemical kinetic reaction in a batch reactor via nonlocal operator with power law kernel, Physica A: Statistical Mechanics and its Applications, 2019, 542. Article ID: 123494. [26] A. Svecic, D. Roberge and S. Kadoury, Prediction of inter-fractional radiotherapy dose plans with domain translation in spatiotemporal embeddings, Cancer Research Journal, 2020, 64. Article ID: 101728. [27] S. Samarasinghe, Neural networks for applied sciences and engineering: from fundamentals to complex pattern recognition, New York: Auerbach Publications, Taylor & Francis Group, 2016. [28] A. Singh and J. N. Rai, Stability analysis of fractional order fuzzy cellular neural networks with leakage delay and time varying delays, Chinese Journal of Physics, 2021, 73, 589–599. doi: 10.1016/j.cjph.2021.07.029 [29] R. Tang, H. Su, et al., Finite-time synchronization of Markovian coupled neural networks with delays via intermittent quantized control: linear programming approach, IEEE Transactions on Neural Networks and Learning Systems, 2022, 33, 5268–5278. doi: 10.1109/TNNLS.2021.3069926 [30] S. Wen, S. Chen and W. Guo, Adaptive global synchronization of a general complex dynamical network with non-delayed and delayed coupling, Physics Letters A, 2008, 372, 6340–6346. doi: 10.1016/j.physleta.2008.08.059 [31] C. Wang, Q. Yang, et al., Synchronization analysis of a class of neural networks with multiple time delays, Journal of Mathematics, 2021, 2021. Article ID: 5573619. [32] X. Wang and Z. Hu, Projective synchronization of fractional order chaotic system based on state observer, International Journal of Modern Physics B, 2012, 26, 304–968. [33] X. Wu and H. Lu, Generalized function projective (lag, anticipated and complete) synchronization between two different complex networks with nonidentical nodes, Communications in Nonlinear Science and Numerical Simulation, 2012, 17, 3005–3021. doi: 10.1016/j.cnsns.2011.10.035 [34] S. Wang, H. Zhang, et al., Finite-time projective synchronization of Caputo type fractional complex-valued delayed neural networks, Mathematics, 2021, 9. Article ID: 1406. [35] C. Wang, Q. Yang, et al., Synchronization analysis of a fractional-order non-autonomous neural network with time delay, Physica A: Statistical Mechanics and Its Applications, 2020, 549. Article ID: 124176. [36] H. Wu, L. Wang, et al., Global Mittag-Leffler projective synchronization for fractional-order neural networks: an LMI-based approach, Advances in Differences Equations, 2016, 2016. Article ID: 132. [37] J. Xiao, Z. Wang, et al., Adaptive pinning control for the projective synchronization of drive-response dynamical networks, Applied Mathematics and Computation, 2012, 219, 2780–2788. doi: 10.1016/j.amc.2012.09.005 [38] X. Yang, C. Li, et al., Quasi-uniform synchronization of fractional-order memristor-based neural networks with delay, Neurocomputing, 2017, 234, 205–215. doi: 10.1016/j.neucom.2017.01.014 [39] J. Yu, C. Hu, et al., Projective synchronization for fractional neural networks, Neural Networks, 2014, 49, 87–95. doi: 10.1016/j.neunet.2013.10.002 [40] X. Yang, C. Li, et al., Synchronization of fractional-order memristor-based complex-valued neural networks with uncertain parameters and time delays, Chaos, Solitons and Fractals, 2018, 110, 105–123. doi: 10.1016/j.chaos.2018.03.016 [41] H. You, Y. Shen, et al., Optimal control and parameters design for the fractional-order vehicle suspension system, Journal of Low Frequency Noise, Vibration and Active Control, 2018, 37, 456–467. doi: 10.1177/0263092317717166 [42] X. Yang, Y. Liu, et al., Synchronization of coupled time-delay neural networks with mode-dependent average dwell time switching, IEEE Transactions on Neural Networks and Learning Systems, 2020, 31, 5483–5496. doi: 10.1109/TNNLS.2020.2968342 [43] Q. Zhu, W. Zhou, et al., Mode-dependent projective synchronization for neutral-type neural networks with distributed time delays, Neurocomputing, 2014, 140, 97–103. doi: 10.1016/j.neucom.2014.03.032 [44] H. Zhang, R. Ye, et al., Lyapunov functional approach to stability analysis of Riemann-Liouville fractional neural networks with time-varying delays, Asian Journal of Control, 2018, 20, 1938–1951. doi: 10.1002/asjc.1675 [45] Z. Zhang, Y. Zhang, et al., Global asymptotical stability analysis for fractional neural networks with time-varying delays, Mathematics, 2019, 7. Article ID: 138. [46] S. Zheng, Pinning and impulsive synchronization control of complex dynamical networks with non-derivative and derivative coupling, Journal of the Franklin Institute-Engineering and Applied Mathematics, 2017, 354, 6341–6363. doi: 10.1016/j.jfranklin.2017.07.041 [47] W. Zhang, J. Cao, et al., Projective synchronization of fractional-order delayed neural networks based on the comparison principle, Advances in Difference Equations, 2018, 2018. Article ID: 73. -
-
Figures(16)
Export File
Citation
Lili Jia, Zongxin Lei, Changyou Wang, Yuqian Zhou, Tao Jiang, Yuanhua Du, Qiuyan Zhang. PROJECTION SYNCHRONIZATION OF FUNCTIONAL FRACTIONAL-ORDER NEURAL NETWORKS WITH VARIABLE COEFFICIENTS[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 1070-1087. doi: 10.11948/20220491
Format
Content
DownLoad:
-
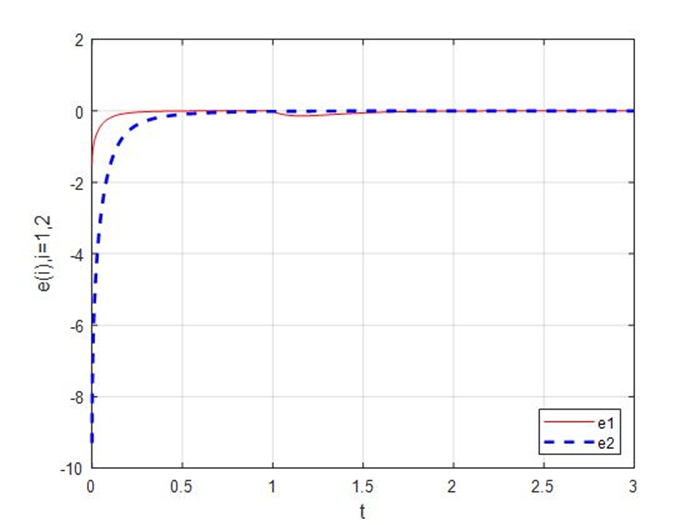
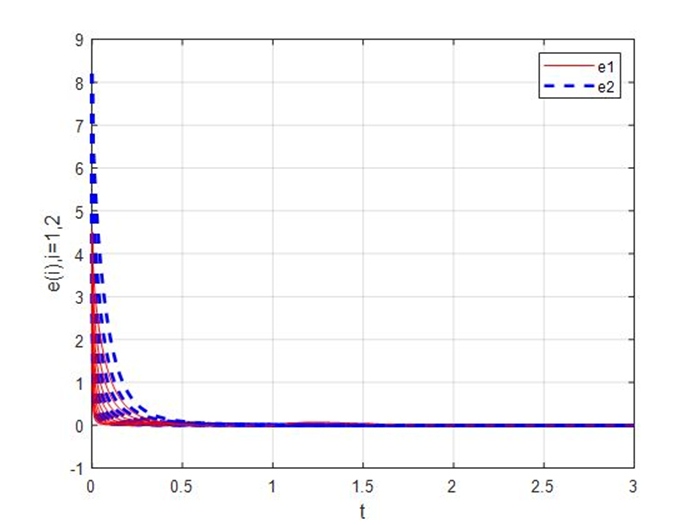
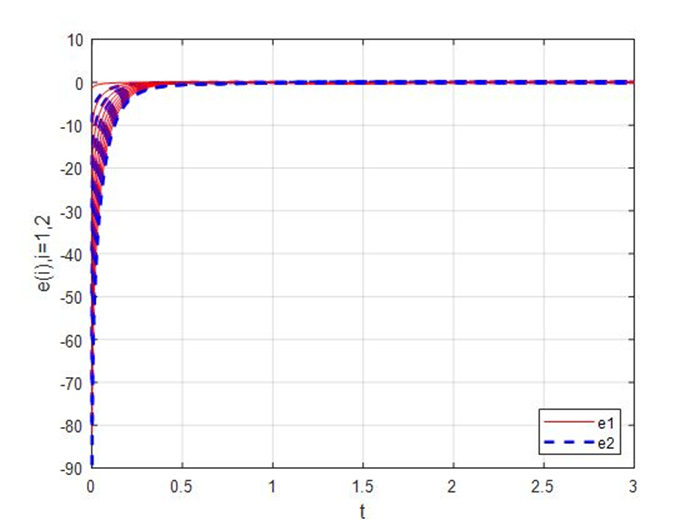
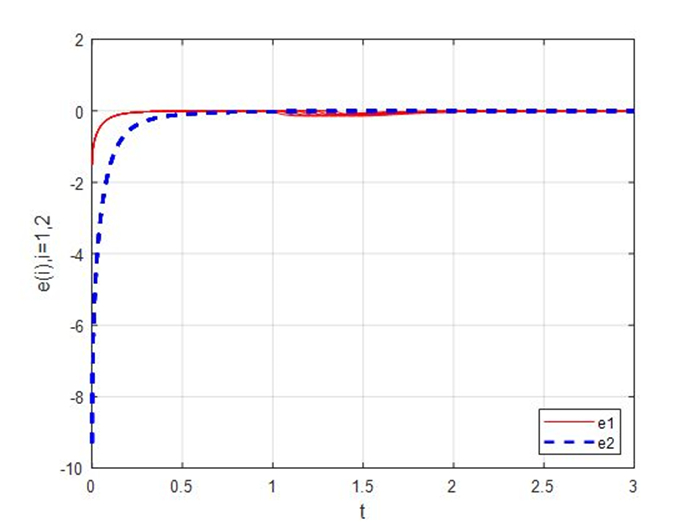
Figure 1.
Synchronization errors of the master-slave systems (4.1) and (4.2) with
$ \beta = -2 $ -
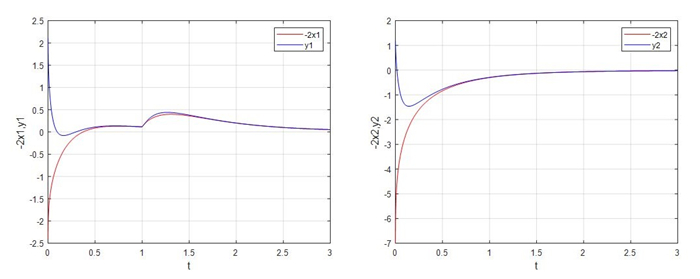
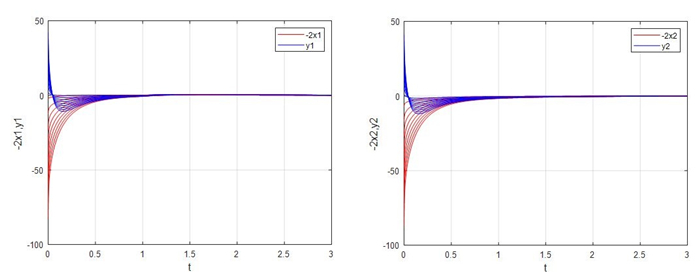
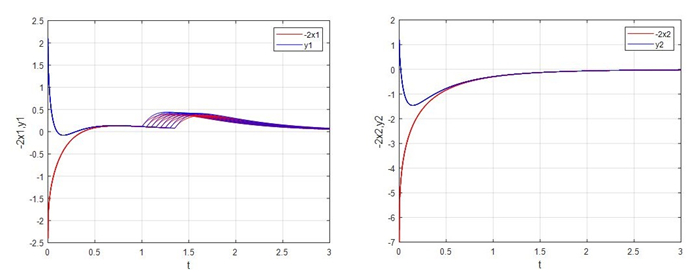
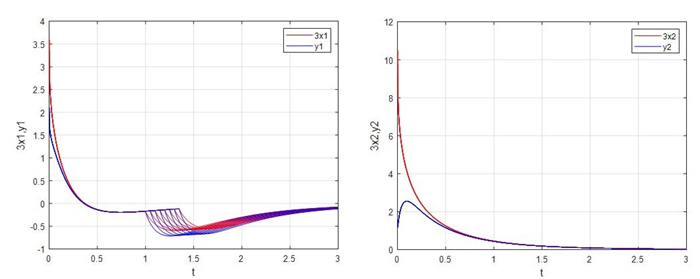
Figure 2.
Evolutions of the master-slave systems (4.1) and (4.2) with
$ \beta = -2 $ -
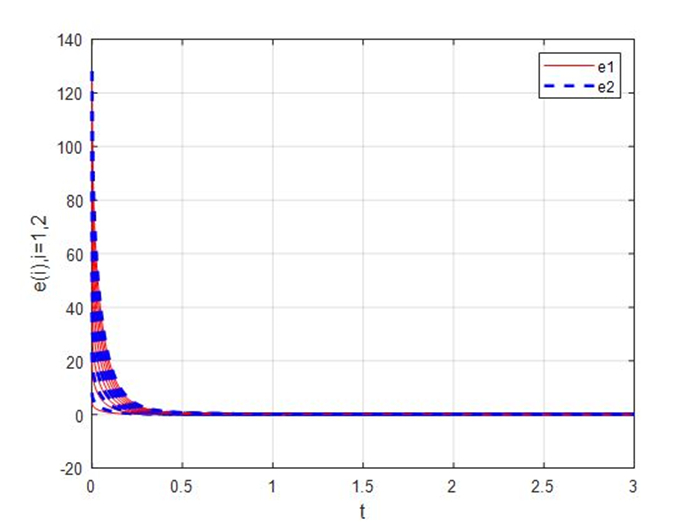
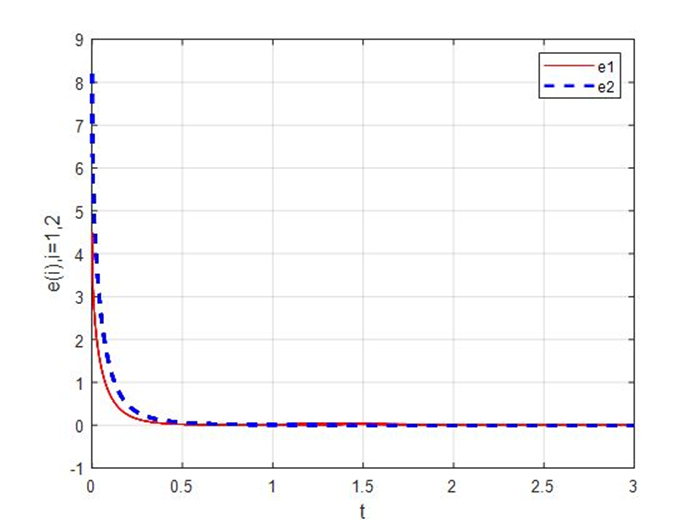
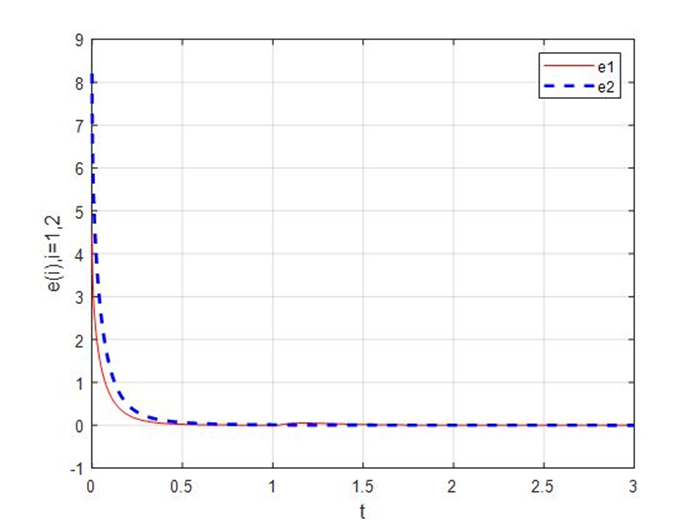
Figure 3.
Synchronization errors of the master-slave systems (4.1) and (4.2) with
$ \beta = 3 $ -
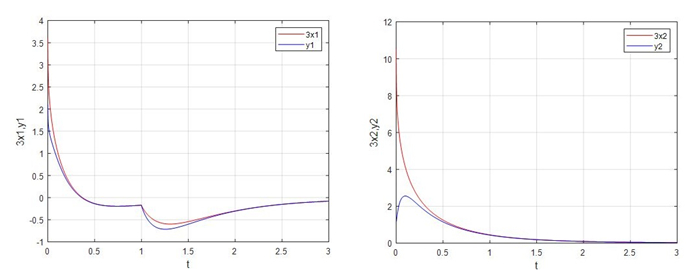
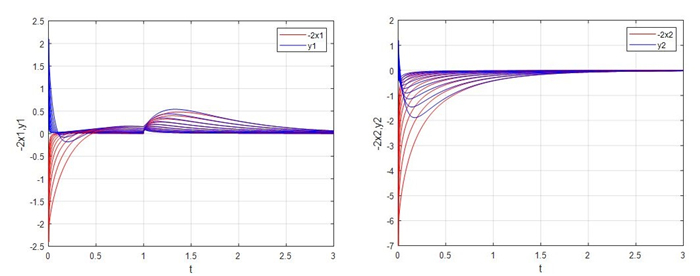
Figure 4.
Evolutions of the master-slave systems (4.1) and (4.2) with
$ \beta = 3 $ -
Figure 5.
Synchronization errors of the systems (4.1) and (4.2) with different initial values and
$ \beta = -2 $ -
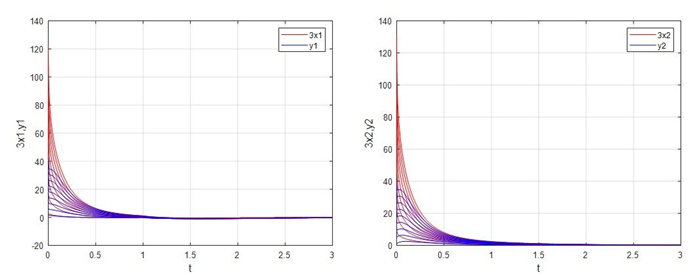
Figure 6.
Evolutions of the master-slave systems (4.1) and (4.2) with different initial values and
$ \beta = -2 $ -
Figure 7.
Synchronization errors of the systems (4.1) and (4.2) with different fractional orders and
$ \beta = -2 $ -
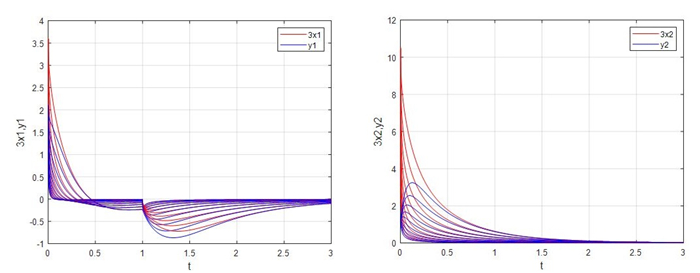
Figure 8.
Evolutions of the master-slave systems (4.1) and (4.2) with different fractional orders and
$ \beta = -2 $ -
Figure 9.
Synchronization errors of the systems (4.1) and (4.2) with different delays and
$ \beta = -2 $ -
Figure 10.
Evolutions of the master-slave systems (4.1) and (4.2) with different delays and
$ \beta = -2 $ -
Figure 11.
Synchronization errors of the systems (4.1) and (4.2) with different initial values and
$ \beta = 3 $ -
Figure 12.
Evolutions of the master-slave systems (4.1) and (4.2) with different initial values and
$ \beta = 3 $ -
Figure 13.
Synchronization errors of the systems (4.1) and (4.2) with different fractional orders and
$ \beta = 3 $ -
Figure 14.
Evolutions of the master-slave systems (4.1) and (4.2) with different fractional orders and
$ \beta = 3 $ -
Figure 15.
Synchronization errors of the systems (4.1) and (4.2) with different delays and
$ \beta = 3 $ -
Figure 16.
Evolutions of the master-slave systems (4.1) and (4.2) with different delays and
$ \beta = 3 $