| Citation: |
Shazia Sadiq, Mujeeb ur Rehman. NUMERICAL TECHNIQUE BASED ON GENERALIZED LAGUERRE AND SHIFTED CHEBYSHEV POLYNOMIALS[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 1977-2001. doi: 10.11948/20220504
|
NUMERICAL TECHNIQUE BASED ON GENERALIZED LAGUERRE AND SHIFTED CHEBYSHEV POLYNOMIALS
-
Abstract
In this study, we present a numerical scheme for solving a class of fractional-order partial differential equations. First, we introduce $ \psi $-Laguerre polynomials, then, we employ $ \psi $-shifted Chebyshev and $ \psi $-Laguerre polynomials for the solution of space-time fractional-order differential equations. In our approach, we project $ \psi $-shifted Chebyshev and $ \psi $-Laguerre polynomials to develop operational matrices of fractional-order integration. The use of these orthogonal polynomials converts the problem under consideration into a system of algebraic equations. The solution of this system provides the unknown matrix which is then used to obtain the approximated numerical solution. Finally, some illustrative examples are included to observe the validity and applicability of the proposed method.
-
-
References
[1] A. E. Abouelregal and H. Ahmad, A modified thermoelastic fractional heat conduction model with a single-lag and two different fractional-orders, J. Appl. Comput. Mech., 2021, 7(3), 1676–1686. DOI: 10.22055/JACM.2020.33790.2287. [2] O. P. Agrawal, Some generalized fractional calculus operators and their applications in integral equations, Fract. Calc. Appl. Anal., 2012, 15(4), 700–711. DOI: 10.2478/s13540-012-0047-7. [3] M. N. Alam, I. Talib and C. Tunç, The new soliton configurations of the 3D fractional model in arising shallow water waves, Int. J. Appl. Comput. Math., 2023, 9(5), 75. doi: 10.1007/s40819-023-01552-0 [4] R. Almeida, A Caputo fractional derivative of a function with respect to another function, Commun. Nonlinear Sci. Numer. Simul., 2017, 44, 460–481. doi: 10.1016/j.cnsns.2016.09.006 [5] R. Almeida, M. Jleli and B. Samet, A numerical study of fractional relaxation-oscillation equations involving $ \psi $-Caputo fractional derivative, Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas, 2019, 113(3), 1873–1891. [6] M. Aslefallah and D. Rostamy, A numerical scheme for solving Space-Fractional equation by finite differences theta-method, Int. J. Adv. Appl. Math. Mech., 2014, 1(4), 1–9. [7] A. Azizi, S. Abdi and J. Saeidian, Applying Legendre wavelet method with Tikhonov regularization for one-dimensional time-fractional diffusion equations, Comput. Appl. Math., 2018, 37(4), 4793–4804. DOI: 10.1007/s40314-018-0593-7. [8] D. Baleanu and A. Fernandez, On fractional operators and their classifications, Mathematics, 2019, 7(9), 830. DOI: 10.3390/math7090830. [9] A. Baseri, S. Abbasbandy and E. Babolian, A collocation method for fractional diffusion equation in a long time with Chebyshev functions, Appl. Math. Comput., 2018, 322, 55–65. DOI: 10.1016/j.amc.2017.11.048. [10] W. W. Bell, Special Functions for Scientists and Engineers, Courier Corporation, 2004. [11] S. A. Bhanotar and M. K. Kaabar, Analytical solutions for the nonlinear partial differential equations using the conformable triple Laplace transform decomposition method, Int. J. Differ. Equ., 2021, 2021. DOI: 10.1155/2021/9988160. [12] J. Biazar and K. Sadri, Two-variable Jacobi polynomials for solving some fractional partial differential equations, J. Comput. Math., 2020, 38, 849–873. DOI: 10.4208/jcm.1906-m2018-0131. [13] S. Bouriah, D. Foukrach, M. Benchohra and J. Graef, Existence and uniqueness of periodic solutions for some nonlinear fractional pantograph differential equations with $ \psi $-Caputo derivative, Arab. J. Math., 2021, 10(3), 575–587. DOI: 10.1007/s40065-021-00343-z. CrossRef $ \psi $-Caputo derivative" target="_blank">Google Scholar
[14] M. Bucelli, M. Salvador and A. Quarteroni, Multipatch isogeometric analysis for electrophysiology: Simulation in a human heart, Comput. Methods. Appl. Mech. Eng., 2021, 376, 113666. DOI: 10.1016/j.cma.2021.113666. [15] H. Dehestani, Y. Ordokhani and M. Razzaghi, Fractional-order Legendre-Laguerre functions and their applications in fractional partial differential equations, Appl. Math. Comput., 2018, 336, 433–453. DOI: 10.1016/j.amc.2018.05.017. [16] K. Diethelm, V. Kiryakova, Y. Luchko, J. T. Machado and V. E. Tarasov, Trends, directions for further research and some open problems of fractional calculus, Nonlinear Dyn., 2022, 107(4), 3245–3270. doi: 10.1007/s11071-021-07158-9 [17] A. Fernandez and D. Baleanu, Classes of operators in fractional calculus: A case study, Math. Methods Appl. Sci., 2021, 44(11), 9143–9162. DOI: 10.1002/mma.7341. [18] R. A. Khan and H. Khalil, A new method based on legendre polynomials for solution of system of fractional order partial differential equations, Int. J. Comput. Math., 2014, 91(12), 2554–2567. DOI: 10.1080/00207160.2014.880781. [19] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier, 204, 2006. [20] E. Kreyszig, Introductory Functional Analysis with Applications, John Wiley and Sons, New York, 1978. [21] S. Kumar, J. F. Gomez Aguilar and P. Pandey, Numerical solutions for the reaction–diffusion, diffusion‐wave, and Cattaneo equations using a new operational matrix for the Caputo–Fabrizio derivative, Math. Methods. Appl. Sci., 2020, 43(15), 8595–8607. DOI: 10.1002/mma.6517. [22] S. Kumbinarasaiah and W. Adel, Hermite wavelet method for solving nonlinear Rosenau-Hyman equation, Partial Differ. Equ. Appl. Math., 2021, 4, 100062. DOI: 10.1016/j.padiff.2021.100062. [23] X. Liang, F. Gao, C. B. Zhou, Z. Wang and X. J. Yang, An anomalous diffusion model based on a new general fractional operator with the Mittag-Leffler function of Wiman type, Adv. Differ. Equ., 2018, 2018(1), 1–11. DOI: 10.1186/s13662-018-1478-1. [24] T. C. Mahor, R. Mishra and R. Jain, Analytical solutions of linear fractional partial differential equations using fractional Fourier transform, J. Comput. Appl. Math., 2021, 385(2021), 113202. DOI: 10.1016/j.cam.2020.113202. [25] S. Mockary, E. Babolian and A. R. Vahidi, A fast numerical method for fractional partial differential equations, Adv. Differ. Equa., 2019, 452(2019). DOI: 10.1186/s13662-019-2390-z. [26] K. M. Owolabi, Computational techniques for highly oscillatory and chaotic wave problems with fractional-order operator, Eur. Phys. J. Plus., 2020, 135(10), 1–23. DOI: 10.1140/epjp/s13360-020-00873-z. [27] O. Postavaru and A. Toma, Numerical solution of two-dimensional fractional-order partial differential equations using hybrid functions, Partial Differ. Equ. Appl. Math., 2021, 4, 100099. DOI: 10.1016/j.padiff.2021.100099. [28] V. M. Rozenbaum, I. V. Shapochkina and L. I. Trakhtenberg, Green's function method in the theory of Brownian motors, Physics-Uspekhi, 2019, 62(5), 496. DOI: 10.3367/UFNe.2018.04.038347. [29] S. Sabermahani, Y. Ordokhani and S. A. Yousefi, Two-dimensional Muntz-Legendre hybrid functions: Theory and applications for solving fractional-order partial differential equations, Comput. Appl. Math., 2020, 39(2), 1–22. DOI: 10.1007/s40314-020-1137-5. [30] S. Sadiq and M. Rehman, Solution of fractional boundary value problems by $ \psi $-shifted operational matrices, AIMS Math., 2022, 7(4), 6669–6693. doi: 10.3934/math.2022372 CrossRef $ \psi $-shifted operational matrices" target="_blank">Google Scholar
[31] S. Sadiq and M. Rehman, $ \psi $-shifted operational matrix scheme for fractional partial differential equations, J. Appl. Anal. Comput., 2022, 12(2), 497–516. DOI: 10.11948/20210101. CrossRef $ \psi $-shifted operational matrix scheme for fractional partial differential equations" target="_blank">Google Scholar
[32] H. Singh and C. S. Singh, Stable numerical solutions of fractional partial differential equations using Legendre scaling functions operational matrix, Ain. Shams Eng. J., 2018, 9(4), 717–725. DOI: 10.1016/j.asej.2016.03.013. [33] J. V. D. C. Sousa and E. C. de Oliveira, On the $ \psi $-Hilfer fractional derivative, Commun. Nonlinear Sci. Numer. Simul., 2018, 60(2018), 72–91. DOI: 10.1016/j.cnsns.2018.01.005. CrossRef $ \psi $-Hilfer fractional derivative" target="_blank">Google Scholar
[34] I. Talib and M. Bohner, Numerical study of generalized modified Caputo fractional differential equations, Int. J. Comput. Math., 2023, 100(1), 153–176. doi: 10.1080/00207160.2022.2090836 [35] I. Talib and F. Ozger, Orthogonal Polynomials based Operational Matrices with Applications to Bagley-Torvik Fractional Derivative Differential Equations, 2023. [36] D. Vivek, E. M. Elsayed and K. Kanagarajan, Theory and analysis of partial differential equations with a $\psi $-Caputo fractional derivative, Rocky Mt. J. Maths., 2019, 49(4), 1355–1370. DOI: 10.1216/RMJ-2019-49-4-1355. [37] B. Zhang, Y. Tang and X. Zhang, Numerical solution of fractional differential equations using hybrid Bernoulli polynomials and block pulse functions, Math. Sci., 2021, 15(3), 293–304. DOI: 10.1007/s40096-021-00379-4. -
-
Figures(16) / Tables(8)
Export File
Citation
Shazia Sadiq, Mujeeb ur Rehman. NUMERICAL TECHNIQUE BASED ON GENERALIZED LAGUERRE AND SHIFTED CHEBYSHEV POLYNOMIALS[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 1977-2001. doi: 10.11948/20220504
Format
Content
DownLoad:
-
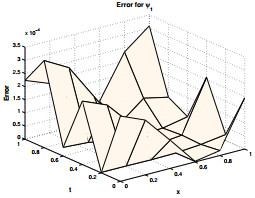
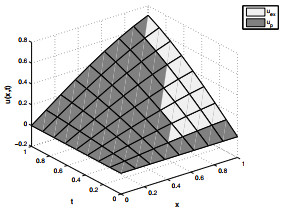
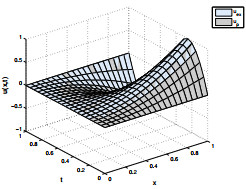
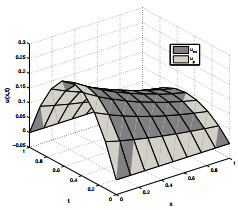
Figure 1.
Exact and proposed solution for
$ \psi_1 $ $ \gamma=1.8, \zeta=1.3 $ $ N=5 $ -
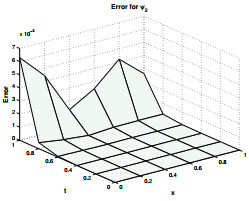
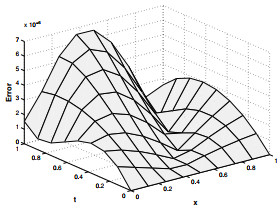
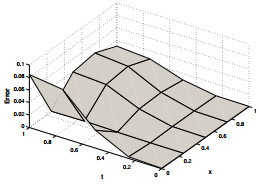
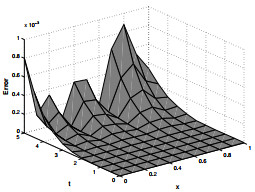
Figure 2.
Absolute error for
$ \psi_2 $ $ \gamma=1.8, \zeta=1.3 $ $ N=5 $ -
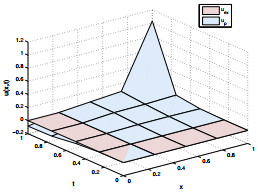
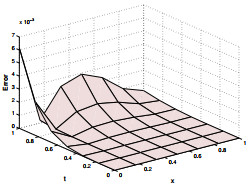
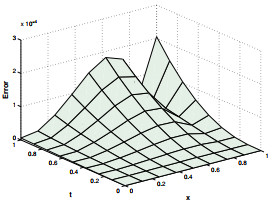
Figure 3.
Absolute error for
$\psi_2$ $\gamma=$ $\zeta=1.3$ $N=5$ -
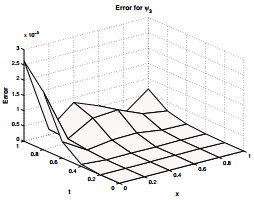
Figure 4.
Absolute error for
$\psi_3$ $\gamma=$ $1.8, \zeta=1.3$ $N=5$ -
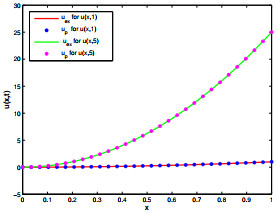
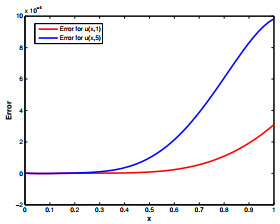
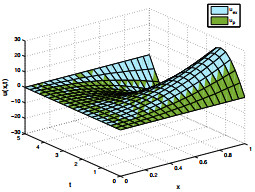
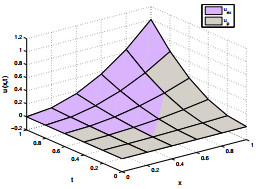
Figure 5.
Exact and proposed solution for
$ u(x, 1) $ $ u(x, 5) $ $ \gamma=2, \zeta=1.5 $ -
Figure 6.
Absolute error for
$u(x, 1)$ $u(x, 5)$ $\gamma=2, \zeta=1.5$ -
Figure 7.
Exact and proposed solution for
$ \gamma=\zeta=1 $ $ N=8 $ -
Figure 8.
Absolute error at
$\gamma=\zeta=1$ $N=8$ -
Figure 9.
Exact and proposed solution for
$ \gamma=0.5, \zeta=2/3 $ $ N=4 $ -
Figure 10.
Absolute error at
$\gamma=$ $0.5, \zeta=2 / 3$ $N=4$ -
Figure 11.
Exact and proposed solution at
$ \gamma=2, \zeta=0.5 $ $ N=6 $ -
Figure 12.
Absolute error at
$\gamma=2, \zeta=0.5$ $N=6$ -
Figure 13.
Exact and proposed solution at
$ \gamma=2, \zeta=0.5 $ $ N=10 $ -
Figure 14.
Absolute error at
$\gamma=2, \zeta=0.5$ $N=10$ -
Figure 15.
Exact and proposed solution at
$ \gamma=1.8, \zeta=1 $ $ N=8 $ -
Figure 16.
Absolute error at
$\gamma=1.8, \zeta=1$ $N=8$