| Citation: | Wenling Wang, Caiqin Song, Wenli Wang. A NEW BCR METHOD FOR COUPLED OPERATOR EQUATIONS WITH SUBMATRIX CONSTRAINT[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2002-2036. doi: 10.11948/20230106 |
A NEW BCR METHOD FOR COUPLED OPERATOR EQUATIONS WITH SUBMATRIX CONSTRAINT
-
Abstract
In the present work, a new biconjugate residual (BCR) algorithm is proposed in order to compute the constraint solution of the coupled operator equations, in which the constraint solution include symmetric solution, reflective solution, centrosymmetric solution and anti-centrosymmetric solution as special cases. When the studied coupled operator equations are consistent, it is proved that constraint solutions can be convergent to the exact solutions if giving any initial complex matrices or real matrices. In addition, when the studied coupled operator equations are not consistent, the least norm constraint solutions above can also be computed by selecting any initial matrices. Finally, some numerical examples are provided for illustrating the effectiveness and superiority of new proposed method.
-

-
References
[1] B. D. O. Anderson and J. B. Moore, Optimal Control: Linear Quadratic Methods, Courier Corporation, 2007. [2] S. Barnett and C. Storey, Some applications of the Lyapunov matrix equation, IMA Journal of Applied Mathematics, 1968, 4(1), 33-42. doi: 10.1093/imamat/4.1.33 [3] A. Bouhamidi and K. Jbilou, A note on the numerical approximate solutions for generalized Sylvester matrix equations with applications, Applied Mathematics and Computation, 2008, 206(2), 687-694. doi: 10.1016/j.amc.2008.09.022 [4] D. C. Chen, Y. N. Zhang and S. Li, Tracking control of robot manipulators with unknown models: A jacobian-matrix-adaption method, IEEE Transactions on Industrial Informatics, 2017, 14(7), 3044-3053. [5] Y. C. Chen, K. Q. Sun, B. Beker and R. Mittra, Unified matrix presentation of Maxwell's and wave equations using generalized differential matrix operators[EM engineering education], IEEE Transactions on Education, 1998, 41(1), 61-69. doi: 10.1109/13.660791 [6] M. Dehghan and M. Hajarian, Finite iterative algorithms for the reflexive and anti-reflexive solutions of the matrix equation A1X1B1+ A2X2B2= C, Mathematical and Computer Modelling, 2009, 49(9-10), 1937-1959. doi: 10.1016/j.mcm.2008.12.014 [7] M. Dehghan and M. Hajarian, On the reflexive solutions of the matrix equation AXB+ CYD= E, Bulletin of the Korean Mathematical society, 2009, 46(3), 511-519. doi: 10.4134/BKMS.2009.46.3.511 [8] M. Dehghan and M. Hajarian. The general coupled matrix equations over generalized bisymmetric matrices, Linear Algebra and its Applications, 2010, 432(6), 1531-1552. doi: 10.1016/j.laa.2009.11.014 [9] M. Delphi and S. Shihab, Operational matrix basic spline wavelets of derivative for linear optimal control problem, Electronics Science Technology and Application, 2019, 6(2), 18-24. [10] Ç. Demir and Ö. Civalek, A new nonlocal FEM via Hermitian cubic shape functions for thermal vibration of nano beams surrounded by an elastic matrix, Composite Structures, 2017, 168, 872-884. doi: 10.1016/j.compstruct.2017.02.091 [11] A. M. Diwekar and R. K. Yedavalli, Smart structure control in matrix second-order form, Smart materials and Structures, 1995, 2442, 24-34. [12] Z. Hailin, An iterative method for symmetric solutions of the matrix equation AXB+ CXD= F, Mathematica Numerica Sinica, 2010. DOI: 10.3788/HPLPB20102206.1351. [13] M. Hajarian, Symmetric solutions of the coupled generalized Sylvester matrix equations via BCR algorithm, Journal of The Franklin Institute, 2016, 353(13), 3233-3248. doi: 10.1016/j.jfranklin.2016.06.008 [14] M. Hajarian, Convergence of HS version of BCR algorithm to solve the generalized Sylvester matrix equation over generalized reflexive matrices, Journal of the Franklin Institute, 2017, 354(5), 2340-2357. doi: 10.1016/j.jfranklin.2017.01.008 [15] E. J. Haug and K. K. Choi, Structural design sensitivity analysis with generalized global stiffness and mass matrices, AIAA journal, 1984, 22(9), 1299-1303. doi: 10.2514/3.8776 [16] Z. H. He, W. L. Qin and X. X. Wang, Some applications of a decomposition for five quaternion matrices in control system and color image processing, Computational and Applied Mathematics, 2021. DOI: 10.1007/S40314-021-01579-3. [17] Z. H. He, X. X. Wang and Y. F. Zhao, Eigenvalues of quaternion tensors with applications to color video processing, Journal of Scientific Computing, 2022. DOI: 10.1007/S10915-022-02058-5. [18] L. Jin, S. Li, B. Hu and J. G. Yu, A noise-suppressing neural algorithm for solving the time-varying system of linear equations: A control-based approach, IEEE Transactions on Industrial Informatics, 2018, 15(1), 236-246. [19] C. Johnson, Numerical Solution of Partial Differential Equations by the Finite Element Method, Courier Corporation, 2012. [20] V. N. Katsikis, S. D. Mourtas, P. S. Stanimirovic and Y. N. Zhang, Solving complex-valued time-varying linear matrix equations via QR decomposition with applications to robotic motion tracking and on angle-of-arrival localization, IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(8), 3415-3424. doi: 10.1109/TNNLS.2021.3052896 [21] L. Lapidus and G. F. Pinder, Numerical solution of partial differential equations in science and engineering, John Wiley & Sons, 1999. [22] W. B. Li, A recurrent neural network with explicitly definable convergence time for solving time-variant linear matrix equations, IEEE Transactions on Industrial Informatics, 2018, 14(12), 5289-5298. doi: 10.1109/TII.2018.2817203 [23] Z. Li and Y. N. Zhang, Improved Zhang neural network model and its solution of time-varying generalized linear matrix equations, Expert Systems with Applications, 2010, 37(10), 7213-7218. doi: 10.1016/j.eswa.2010.04.007 [24] C. Q. Lv and C. F. Ma, BCR method for solving generalized coupled Sylvester equations over centrosymmetric or anti-centrosymmetric matrix, Computers & Mathematics with Applications, 2018, 75(1), 70-88. [25] V. Mehrmann, Matrix analysis for scientists and engineers[Book Review], IEEE Control Systems Magazine, 2006, 26(2), 94-95. doi: 10.1109/MCS.2006.1615276 [26] N. Mikaeilvand, On solvability of fuzzy system of linear matrix equations, J. Appl. Sci. Res., 2011, 7(2), 141-153. [27] Y. X. Peng, X. Y. Hu and L. Zhang, An iteration method for the symmetric solutions and the optimal approximation solution of the matrix equation AXB= C, Applied Mathematics and Computation, 2005, 160(3), 763-777. doi: 10.1016/j.amc.2003.11.030 [28] Z. H. Peng, The reflexive least squares solutions of the matrix equation A1X1B1+ A2X2B2+…+ AlXlBl= C with a submatrix constraint, Numerical Algorithms, 2013, 64(3), 455-480. doi: 10.1007/s11075-012-9674-7 [29] Z. Y. Peng, An iterative method for the least squares symmetric solution of the linear matrix equation AXB= C, Applied Mathematics and Computation, 2005, 170(1), 711-723. doi: 10.1016/j.amc.2004.12.032 [30] S. Sana and V. S. Rao, Application of linear matrix inequalities in the control of smart structural systems, Journal of intelligent material systems and structures, 2000, 11(4), 311-323. doi: 10.1106/E2AY-BY64-H0E4-WRHQ [31] C. Q. Song, Iterative method to the coupled operator matrix equations with sub-matrix constraint and its application in control, Transactions of the Institute of Measurement and Control, 2021, 43(3), 597-611. doi: 10.1177/0142331220947560 [32] M. T. Vespucci and C. G. Broyden, Implementation of different computational variations of biconjugate residual methods, Computers & Mathematics with Applications, 2001, 42(8-9), 1239-1253. [33] L. Xiao, B. L. Liao, S. Li and K. Chen, Nonlinear recurrent neural networks for finite-time solution of general time-varying linear matrix equations, Neural Networks, 2018, 98, 102-113. doi: 10.1016/j.neunet.2017.11.011 [34] Y. J. Xie, N. Huang and C. F. Ma, Iterative method to solve the generalized coupled Sylvester-transpose linear matrix equations over reflexive or anti-reflexive matrix, Computers and Mathematics with Applications, 2014, 67(11), 2071-2084. doi: 10.1016/j.camwa.2014.04.012 [35] Y. J. Xie and C. F. Ma, Iterative methods to solve the generalized coupled Sylvester-conjugate matrix equations for obtaining the centrally symmetric (centrally antisymmetric) matrix solutions, Journal of Applied Mathematics, 2014, 2014(1), 1-17. [36] C. F. Yi, Y. H. Chen and Z. L. Lu, Improved gradient-based neural networks for online solution of Lyapunov matrix equation, Information processing letters, 2011, 111(16), 780-786. doi: 10.1016/j.ipl.2011.05.010 [37] S. W. Yu, Z. H. He, T. C. Qi and X. X. Wang, The equivalence canonical form of five quaternion matrices with applications to imaging and Sylvester-type equations, Journal of Computational and Applied Mathematics, 2021. DOI: 10.1016/J.CAM.2021.113494. [38] H. M. Zhang, A finite iterative algorithm for solving the complex generalized coupled Sylvester matrix equations by using the linear operators, Journal of the Franklin Institute, 2017, 354(4), 1856-1874. doi: 10.1016/j.jfranklin.2016.12.011 [39] J. F. Zhang, Optimal control for mechanical vibration systems based on second-order matrix equations, Mechanical Systems and Signal Processing, 2002, 16(1), 61-67. doi: 10.1006/mssp.2001.1441 -
-
-
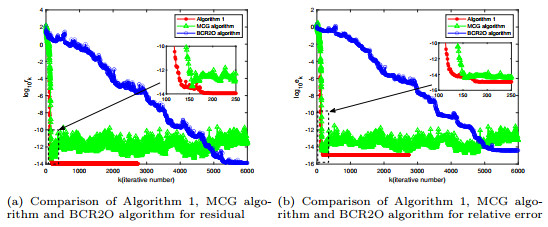
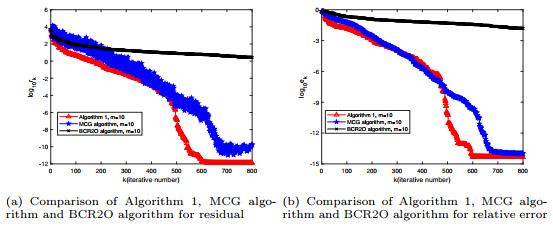
Figure 1.
Comparison of convergence curves for Example 4.1
-
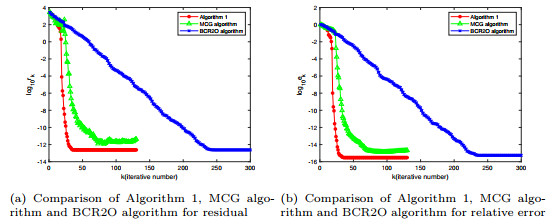
Figure 2.
Comparison of convergence curves for Example 4.2
-
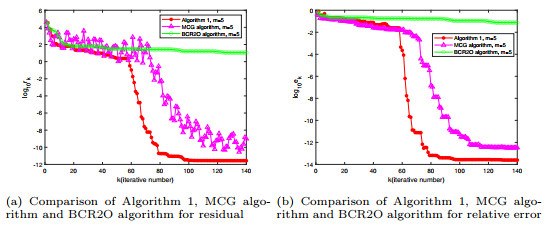
Figure 3.
Comparison of convergence curves for Example 4.3
-
Figure 4.
Comparison of convergence curves for Example 4.4
-
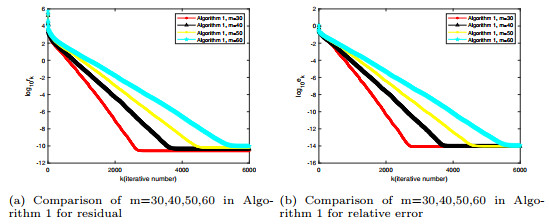
Figure 5.
Comparison of convergence curves for different values of
$ m $




 DownLoad:
DownLoad: