| Citation: |
A.N. Nirmala, S. Kumbinarasaiah. NUMERICAL APPROACH FOR THE HUNTER SAXTON EQUATION ARISING IN LIQUID CRYSTAL MODEL THROUGH COCKTAIL PARTY GRAPHS CLIQUE POLYNOMIAL[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2037-2062. doi: 10.11948/20230114
|
NUMERICAL APPROACH FOR THE HUNTER SAXTON EQUATION ARISING IN LIQUID CRYSTAL MODEL THROUGH COCKTAIL PARTY GRAPHS CLIQUE POLYNOMIAL
-
Abstract
In this paper, a well-known nematic liquid crystal model, the Hunter Saxton equation, is solved by the new graph theoretic polynomial approach. At first, we extracted the clique polynomials from the cocktail party graph (CPG) and generated the generalized operational matrix of integration through the clique polynomials of CPG. Then, an effective computational technique called the cocktail party graphs clique polynomial collocation method (CCCM) is developed to obtain an approximate numerical solution for the nonlinear Hunter-Saxton equation (HSE). The operational matrix of CPG reduces the HSE into an algebraic system of nonlinear equations that makes the solution relatively superficial. The Newton-Raphson method solves these nonlinear algebraic equations to obtain the clique polynomial solution for HSE. The efficiency of the CCCM is illustrated by examining two numerical examples. The solution of the HSE is presented through figures and tables for different values of x,t, and N. The convergence analysis, tabulated results of numerical comparison of absolute errors of CCCM with the recent numerical methods, and error norms projected that, CCCM is considerably efficacious on the computational ground for higher accuracy and convergence of numerical solutions.
-
-
References
[1] W. Adel and S. Kumbinarasaiah, A new clique polynomial approach for fractional partial differential equations, International Journal of Nonlinear Sciences and Numerical Simulation, 2022, 11(0). [2] I. Ahmad, H. Ilyas, K. Kutlu, V. Anam, S. I. Hussain and J. L. Guirao, Numerical computing approach for solving hunter-saxton equation arising in liquid crystal model through sinc collocation method, Heliyon, 2021, 7(7). [3] S. Arbabi, A. Nazari and M. T. Darvishi, A Semi-Analytical Solution of Hunter–Saxton Equation, Optik, 2016, 127(13), 5255-5258. doi: 10.1016/j.ijleo.2016.02.065 [4] S. S. Behzadi, Numerical solution of hunter-saxton equation using iterative methods, J. Inform. Math. Sci., 2011, 3, 127-143. [5] A. Bressan, H. Holden and X. Raynaud, Lipschitz metric for the hunter–saxton equation, Journal de mathématiques pures et appliquées, 2010, 94(1), 68-92. doi: 10.1016/j.matpur.2010.02.005 [6] C. J. Cotter, J. Deasy and T. Pryer, The r-Hunter–Saxton equation, smooth and singular solutions and their approximation, Nonlinearity, 2020, 33(12), 7016. doi: 10.1088/1361-6544/abab4d [7] R. M. Ganji, H. Jafari, M. Kgarose and A. Mohammadi, Numerical solutions of time-fractional Klein-Gordon equations by clique polynomials, Alexandria Engineering Journal, 2021, 60(5), 4563-4571. doi: 10.1016/j.aej.2021.03.026 [8] H. Hajiabolhassan and M. L. Mehrabadi, On clique polynomials, Australasian Journal of Combinatorics, 1998, 18, 313-316. [9] M. S. Hashmi, M. Awais, A. Waheed and Q. Ali, Numerical treatment of hunter saxton equation using cubic trigonometric b-spline collocation method, AIP Advances, 2017, 7(9). [10] M. H. Heydari and M. Razzaghi, Highly accurate solutions for space–time fractional schrödinger equations with a non-smooth continuous solution using the hybrid clique functions, Mathematical Sciences, 2023, 17(1), 31-42. doi: 10.1007/s40096-021-00437-x [11] K. J. Hunter and R. Saxton, Dynamics of director fields, SIAM Journal on Applied Mathematics, 1991, 51, 1498-1521. doi: 10.1137/0151075 [12] H. Jafari, R. M. Ganji, S. M. Narsale, M. Kgarose and V. T. Nguyen, Application of hosoya polynomial to splve a class of time-fractional diffusion equations, Fractals, 2023, 2340059. [13] B. Karaagac and A. Esen, The hunter‐saxton equation: A numerical approach using collocation method, Numerical Methods for Partial Differential Equations, 2018, 34(5), 1637-1644. doi: 10.1002/num.22199 [14] A. Kaur, V. Kanwar and H. Ramos, An efficient algorithm combining an optimized hybrid block method and the differential quadrature method for solving hunter–saxton equation, Journal of Mathematical Chemistry, 2023, 61(4), 761-776. doi: 10.1007/s10910-022-01437-5 [15] S. Kumbinarasaiah and K. R. Raghunatha, Study of special types of boundary layer natural convection flow problems through the clique polynomial method, Heat Transfer, 2022, 51(1), 434-450. doi: 10.1002/htj.22314 [16] S. Kumbinarasaiah, H. S. Ramane, K. S. Pise and G. Hariharan, Numerical-solution-for-nonlinear-klein–gordon equation via operational-matrix by clique polynomial of complete graphs, International Journal of Applied and Computational Mathematics, 2021, 7, 1-9. [17] S. Kumbinarasaiah, H. Rezazadeh and W. Adel, Numerical investigation based on laguerre wavelet for solving the hunter Saxton equation, International Journal of Applied and Computational Mathematics, 2020, 1-14. [18] Ö. K. Kürkçü, E. Aslan and M. Sezer, An advanced method with convergence analysis for solving space-time fractional partial differential equations with multi delays, The European Physical Journal Plus, 2019, 134, 1-15. doi: 10.1140/epjp/i2019-12286-x [19] K. Parand and M. Delkhosh, An efficient numerical solution of nonlinear hunter–saxton equation, Communications in Theoretical Physics, 2017, 67(5), 483. doi: 10.1088/0253-6102/67/5/483 [20] A. Prathik, K. Uma and J. Anuradha, An Overview of the application of graph theory, International Journal of ChemTech Research, 2016, 9(2), 242-248. [21] S. Salati, M. Matinfar and H. Jafari, A numerical approach for solving bagely-torvik and fractional oscillation equations, Advanced Mathematical Models and Applications, 2023, 8(2). [22] M. C. Shanmukha, S. Lee, A. Usha, K. C. Shilpa and M. Azeem, Structural descriptors of anthracene using topological indices through CoM-polynomial, Journal of Intelligent and Fuzzy Systems, Preprint, 2023, 1-12. [23] Y. Shi, M. Dehmer, X. Li and I. Gutman, eds., Graph Polynomials, CRC Press, 2016. [24] H. M. Srivastava, F. A. Shah and N. A. Nayied, Fibonacci wavelet method for the solution of the nonlinear hunter–saxton equation, Applied Sciences, 2022, 12(15), 7738. doi: 10.3390/app12157738 [25] R. Ullah, I. Ali, S. Shaheen, T. Khan, F. Faiz and H. Rahman, A mesh-free collocation method based on rbfs for the numerical solution of hunter–saxton and gardner Equations, Mathematical Problems in Engineering, 2022, 2022. [26] H. Wu, Y. Wang and W. Zhang, Numerical solution of a class of nonlinear partial differential equations by using barycentric interpolation collocation method, Mathematical Problems in Engineering, 2018, 2018, 1-10. [27] Y. Xu and C. W. Shu, Dissipative numerical methods for the hunter-saxton equation, Journal of Computational Mathematics, 2010, 606-620. [28] A. Zhang, R. M. Ganji, H. Jafari, M. N. Ncube and L. Agamalieva, Numerical solution of distributed order integro-differential equations, Fractals, 2022, 30(05), 2240123. doi: 10.1142/S0218348X22401235 [29] Z. Zhao, Conservation laws and nonlocally related systems of the hunter–saxton equation for liquid crystal, Analysis and Mathematical Physics, 2019, 2311-2327. [30] P. Zhou, H. Jafari, R. M. Ganji and S. M. Narsale, Numerical study for a class of time-fractional diffusion equations using operational matrices based on hosoya polynomial, Electronic Research Archive, 2023, 31(8), 4530-4548. doi: 10.3934/era.2023231 -
-
Figures(14) / Tables(12)
Export File
Citation
A.N. Nirmala, S. Kumbinarasaiah. NUMERICAL APPROACH FOR THE HUNTER SAXTON EQUATION ARISING IN LIQUID CRYSTAL MODEL THROUGH COCKTAIL PARTY GRAPHS CLIQUE POLYNOMIAL[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2037-2062. doi: 10.11948/20230114
Format
Content
DownLoad:
-
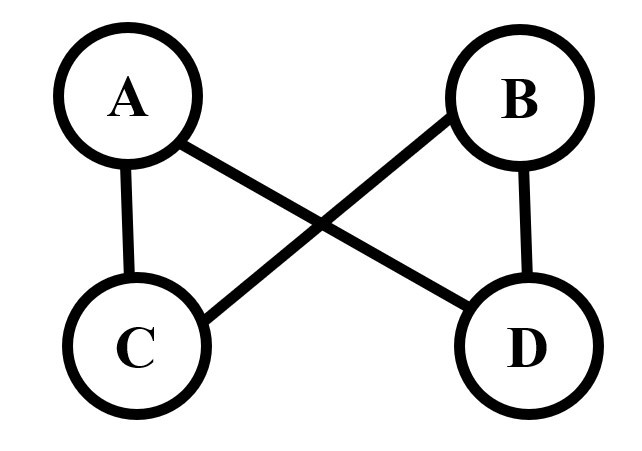
Figure 1.
Graph
$ G_{1} $ -
Figure 2.
Graph
$ G_{2} $ -
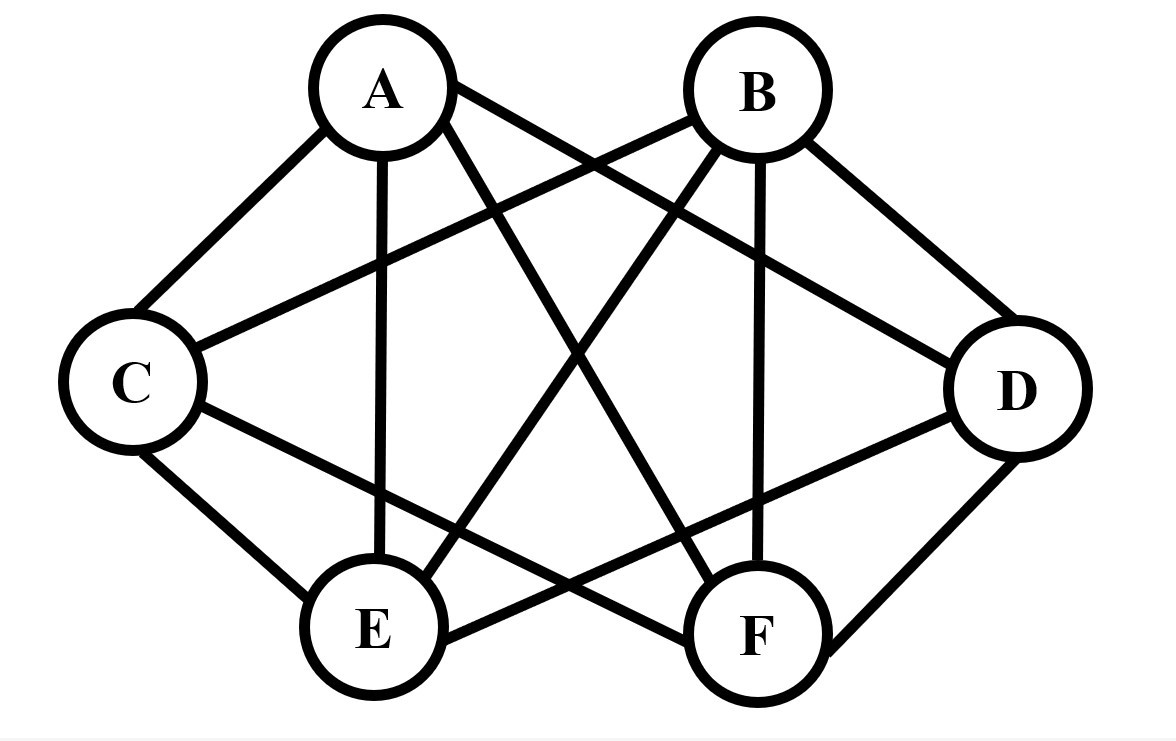
Figure 3.
Graph
$ G_{3} $ -
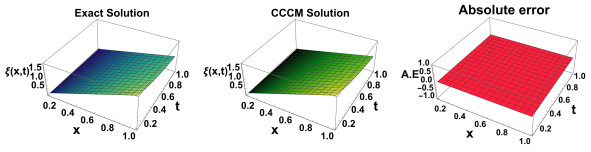
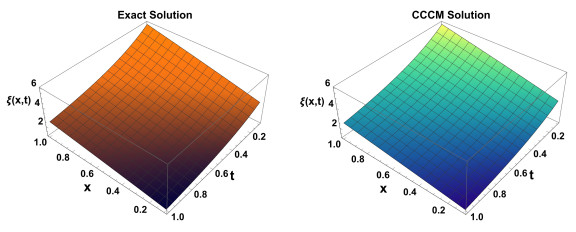
Figure 4.
Graphical representation of the Exact, CCCM solution along with its absolute error at N = 4 (Example 5.1).
-
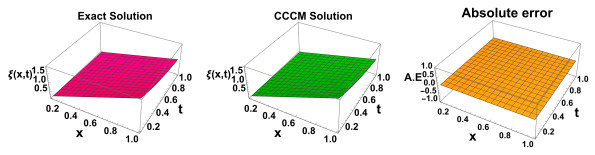
Figure 5.
Graphical representation of the Exact, CCCM solution along with its absolute error at N = 10 (Example 5.1).
-
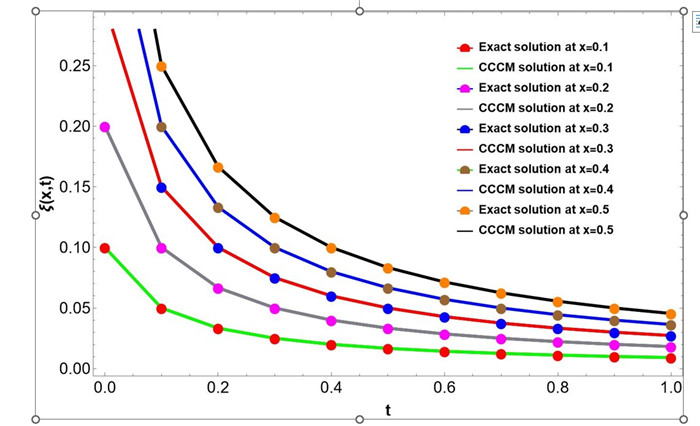
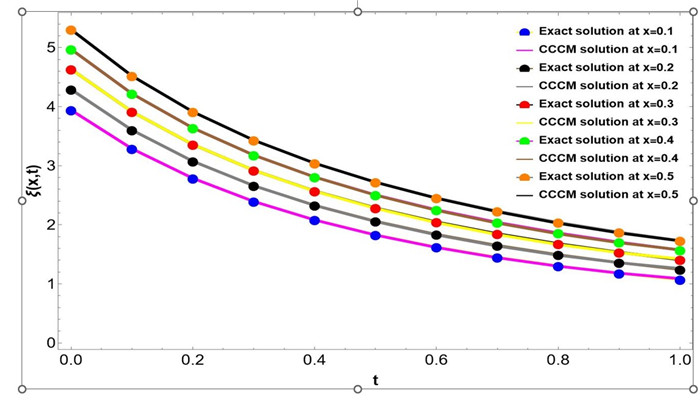
Figure 6.
Graphical representation of the Exact, CCCM solution at fixed
$ x=0.1,0.2,0.3,0.4,0.5 $ $ t \in [0,1], \Delta t=0.1 $ $ N=4 $ -
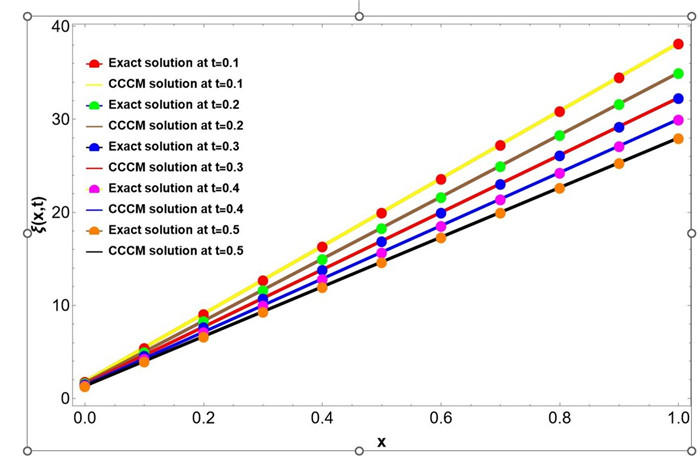
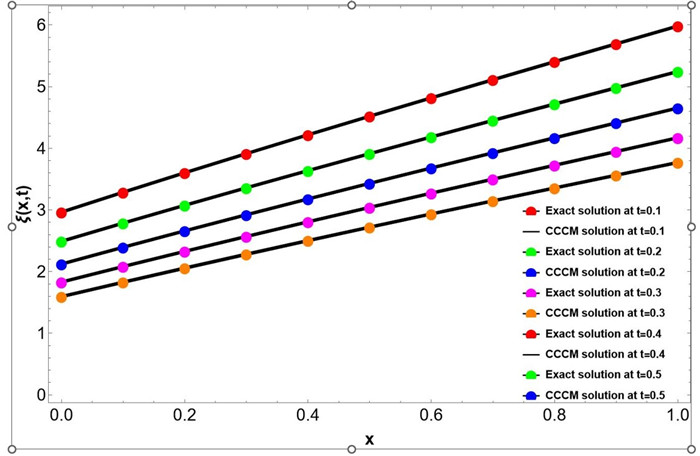
Figure 7.
Graphical representation of the Exact CCCM solution at
$ N=10 $ $ t=0.1,0.2,0.3,0.4,0.5 $ $ x \in [0,1], \Delta x=0.1 $ -
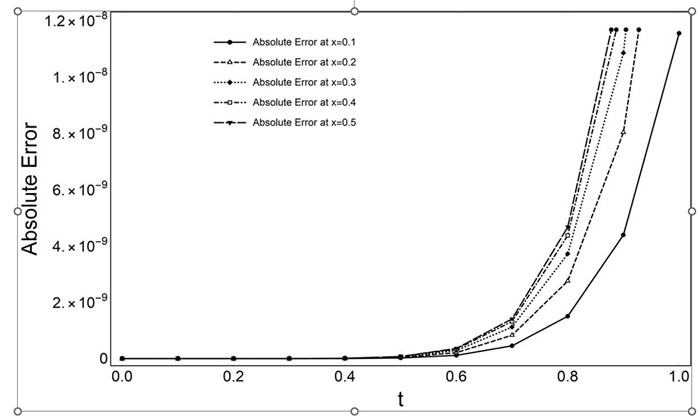
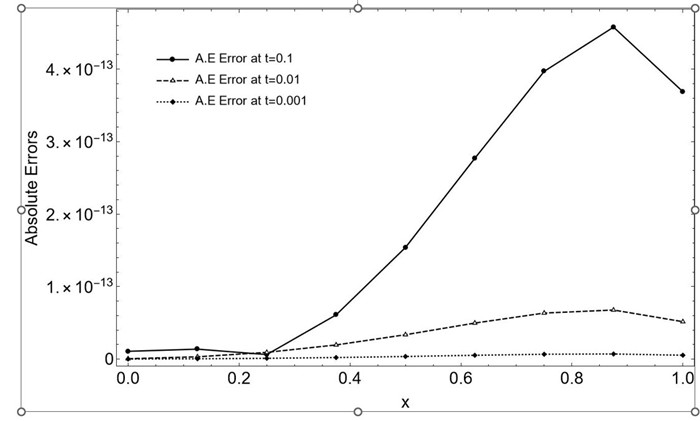
Figure 8.
Graphical representation of Absolute errors of Example 5.1 at
$ N =3 $ $ t \in [0,1], \Delta t=0.1 $ $ x=0.1,0.2,0.3,0.4,0.5 $ -
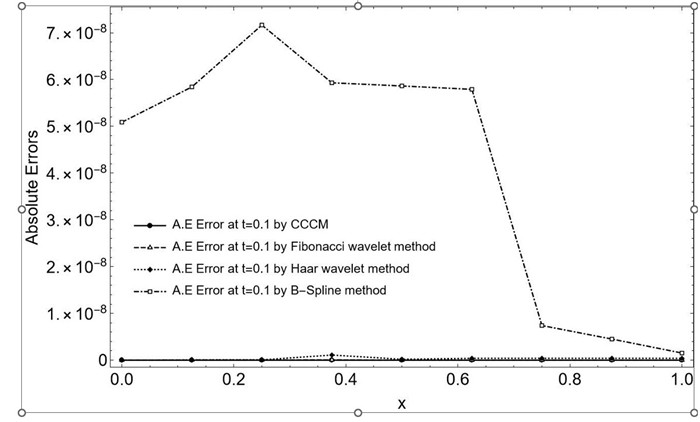
Figure 9.
Graphical representation of comparison of absolute errors of various numerical methods for Example 5.1 at
$ x \in [0,1], \Delta x=0.1, t=0.1,N=3 $ -
Figure 10.
Graphical representation of the Exact, CCCM solution obtained at
$ N =4, t=0.1, x \in [0,1], \Delta x=0.1 $ -
Figure 11.
Graphical representation of the Exact, and CCCM solution at
$ x=0.1,0.2,0.3,0.4,0.5. (N =4) $ -
Figure 12.
Graphical representation of the Exact, CCCM solution at
$ t=0.1,0.2,0.3,0.4,0.5. $ $ N=4 $ -
Figure 13.
Graphical representation of absolute errors for Example 5.2 at
$ x \in [0,1] $ $ t=0.1,0.01,0.001, N=4 $ -
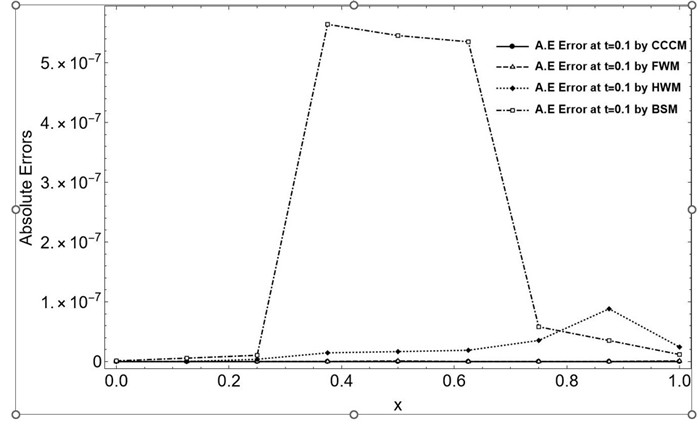
Figure 14.
Graphical representation of comparison of absolute errors of CCCM, Fibonacci wavelet method(FWM), Haar wavelet method(HWM)), B-spline method(BSM) at
$ t=0.1 , N=2, x \in [0,1] $