| Citation: | Chirasak Mongkolkeha, Wutiphol Sintunavarat. ON LARGE S-SIMULATION FUNCTIONS AND LARGE $ \mathcal{Z}_S$-CONTRACTIONS WITH THE LINK TO PICARD MAPPINGS[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3046-3060. doi: 10.11948/20220508 |
ON LARGE S-SIMULATION FUNCTIONS AND LARGE $ \mathcal{Z}_S$-CONTRACTIONS WITH THE LINK TO PICARD MAPPINGS
-
Abstract
The main aim of this paper is to introduce new ideas, called large $s$-simulation functions and large $\mathcal{Z}_s$-contractions, which are inspired by the broad utility of applications of fixed point results for the enlarged class of nonlinear mappings. Illustrative examples supporting the new idea of large $s$-simulation functions are presented. Moreover, fixed point results for large $\mathcal{Z}_s$-contractions are investigated.
-

-
References
[1] S. Banach, Sur les operations dans les ensembles abstrait et leur application aux equations integrals, Fund. Math., 1922, 3, 133–181. doi: 10.4064/fm-3-1-133-181 [2] V. Berinde and M. Pacurar, The early developments in fixed point theory on b-metric spaces: A brief survey and some important related aspects, Carrpathian J. Math., 2022, 38(3), 523–538. doi: 10.37193/CJM.2022.03.01 [3] M. Boriceanu, M. Bota and A. Petrusel, Multivalued fractals in b-metric spaces, Cent. Eur. J. Math., 2010, 8(2), 367–377. [4] M. Bota, A. Molnar and V. Csaba, On Ekeland's variational principle in b-metric spaces, Fixed Point Theory, 2011, 12, 21–28. [5] T. A. Burton, Integral equations, implicit relations and fixed points, Proc. Amer. Math. Soc., 1996, 124, 2383–2390. doi: 10.1090/S0002-9939-96-03533-2 [6] S. Czerwik, Contraction mappings in b-metric spaces, Acta Math. Inform. Univ. Ostrav., 1993, 1, 5–11. [7] S. Czerwik, Nonlinear set-valued contraction mappings in b-metric spaces, Atti Semin. Mat. Fis. Univ. Modena, 1998, 46, 263–276. [8] A. Dehiciy, M. B. Mesmouliz and E. Karapinar, On the fixed points of large-Kannan contraction mappings and applications, Applied Mathematics E-Notes, 2019, 19, 535–551. [9] F. Khojasteh, S. Shukla and S. Radenovic, A new approach to the study of fixed point theory for simulation functions, Filomat, 2015, 29(6), 1189–1194. doi: 10.2298/FIL1506189K [10] A. F. Roldán López de Hierro, E. Karapınar, C. Roldán López de Hierro and J. Martínez-Moreno, Coincidence point theorems on metric spaces via simulation functions, Journal of Computational and Applied Mathematics, 2015, 275, 345–355. doi: 10.1016/j.cam.2014.07.011 [11] K. Sawangsup and W. Sintunavarat, On solving nonlinear matrix equations in terms of b-simulation functions in b-metric spaces with numerical solutions, Computational and Applied Mathematics, 2018, 37, 5829–5843. doi: 10.1007/s40314-018-0664-9 [12] W. Sintunavarat, Nonlinear integral equations with new admissibility types in b-metric spaces, Journal of Fixed Point Theory and Applications, 2016, 18(2), 397–416. doi: 10.1007/s11784-015-0276-6 [13] W. Sintunavarat, Fixed point results in b-metric spaces approach to the existence of a solution for nonlinear integral equations, Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas, 2016, 110(2), 585–600. doi: 10.1007/s13398-015-0251-5 [14] C. Suanoom, W. Khuangsatung and T. Bantaojai, On an open problem in complex valued rectangular b-metric spaces with an application, Science and Technology Asia, 2022, 27(2), 78–83. doi: 10.22517/23447214.24780 [15] O. Yamaod and W. Sintunavarat, An approach to the existence and uniqueness of fixed point results in b-metric spaces via s-simulation functions, Journal of Fixed Point Theory and Applications, 2017, 19, 2819–2830. doi: 10.1007/s11784-017-0453-x -
-
-
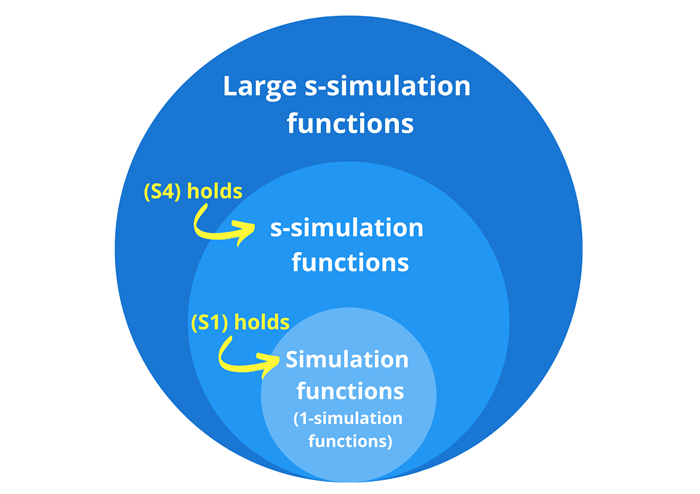
Figure 1.
The relation of various types of simulations.
-
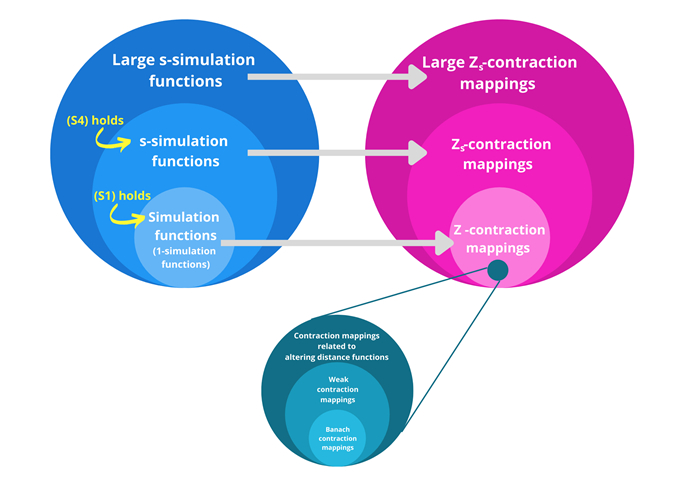
Figure 2.
The relation of classes of important generalized contraction mappings.
-
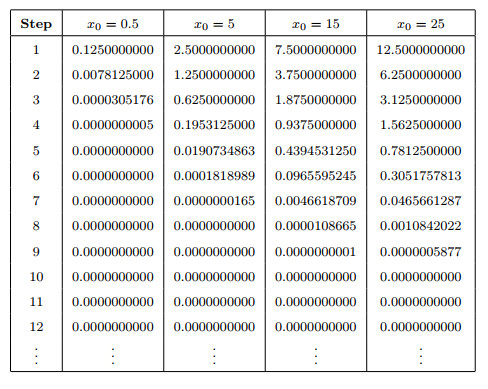
Figure 3.
Comparative results of Picard iterations with initial points
$ x_0=0.5, 5, 15, 25 $ -
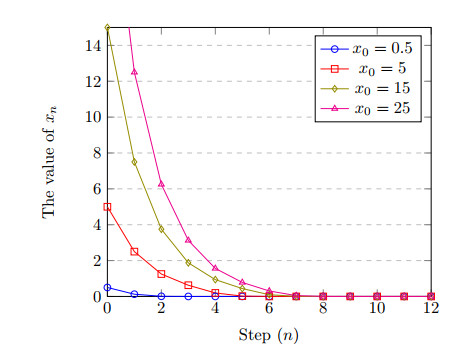
Figure 4.
Behavior of the Picard iteration with initial points
$ x_0 = 0.5, 5, 15, 25 $




 DownLoad:
DownLoad: