| Citation: |
Mohammed Abdel-Aty, Mohammed Abdou. ANALYTICAL AND NUMERICAL DISCUSSION FOR THE PHASE-LAG VOLTERRA-FREDHOLM INTEGRAL EQUATION WITH SINGULAR KERNEL[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3203-3220. doi: 10.11948/20220547
|
ANALYTICAL AND NUMERICAL DISCUSSION FOR THE PHASE-LAG VOLTERRA-FREDHOLM INTEGRAL EQUATION WITH SINGULAR KERNEL
-
Abstract
In this paper, we studied the existence and unique solution of the Volterra-Fredholm integral equation of the second kind (V-FIESK). The general singular kernel is considered to be in position with the Fredholm integral term. Singular kernel will tend to a logarithmic function under exceptional conditions and new discussions. The Volterra-Fredholm integral equation with the logarithmic form will be solved using Legendre polynomials, where the kernel of Volterra integral term is a positive continuous function in time. A system of infinite linear algebraic equations is obtained by solving the problem in series, where the convergence of this system is discussed. Finally, The error is calculated using Maple software after the numerical results have been acquired.
-
-
References
[1] M. A. Abdel-Aty, M. A. Abdou and A. A. Soliman, Solvability of quadratic integral equations with singular kernel, J. of Contemporary Mathematical Analysis, 2022, 57(1), 12-25. DOI: 10.3103/S1068362322010022. [2] M. A. Abdou, M. E. Nasr and M. A. Abdel-Aty, A study of normality and continuity for mixed integral equations, J. of Fixed Point Theory Appl., 2018, 20(1), 1-19. doi: 10.1007/s11784-018-0489-6 [3] M. A. Abdou, A. A. Soliman and M. A. Abdel–Aty, Analytical results for quadratic integral equations with phase–lag term, J. of Applied Analysis & Computation, 2020, 20(4), 1588-1598. DOI: 10.11948/20190279. [4] H. Adibi and P. Assari, Chebyshev wavelet method for numerical solution of Fredholm integral equations of the first kind, Math. Probl. Eng., 2010, 2010, 1-17. DOI: 10.1155/2010/138408. [5] A. Akbarzadeh, J. Fu and Z. Chen, Three-phase-lag heat conduction in a functionally graded hollow cylinder, Trans. Can. Soc. Mech. Eng., 2014, 38(1), 155-171. DOI: 10.1139/tcsme-2014-0010. [6] S. András, Weakly singular Volterra and Fredholm-Volterra integral equations, Stud. Univ. Babes-Bolyai Math., 2003, 48(3), 147-155. [7] N. K. Artiunian, Plane contact problem of the theory of creef, Appl. Math. Mech., 1959, 23, 901-923. [8] K. E. Atkinson, The Numerical Solution of Integral Equation of the Second Kind, Cambridge Monographs on Applied and Computational Mathematics, 1997. [9] Z. Avazzadeh and M. Heydari, Chebyshev polynomials for solving two dimensional linear and nonlinear integral equations of the second kind, Comput. Appl. Math., 2012, 31(1), 127-142. DOI: 10.1590/S1807-03022012000100007. [10] E. Babolian, K. Maleknejad, M. Mordad and B. Rahimi, A numerical method for solving Fredholm-Volterra integral equations in two-dimensional spaces using block pulse functions and an operational matrix, J. Comput. Appl. Math., 2011, 235(14), 3965-3971. DOI: 10.1016/j.cam.2010.10.028. [11] E. Babolian and A. Shahsavaran, Numerical solution of nonlinear Fredholm integral equations of the second kind using Haar wavelets, J. Comput. Appl. Math., 2009, 225(1), 87-95. DOI: 10.1016/j.cam.2008.07.003. [12] H. Brunner, On the numerical solution of nonlinear Volterra-Fredholm integral equations by collocation methods, SIAM J. Numer. Anal., 1990, 27(4), 987-1000. DOI: 10.1137/0727057. [13] S. Chiriţă, On the time differential dual-phase-lag thermoelastic model, Meccanica, 2017, 52(1-2), 349-361. DOI: 10.1007/s11012-016-0414-2. [14] L. M. Delves and J. L. Mohamed, Computational Methods for Integral Equations, New York, London, Cambridge, 1985. [15] R. O. A. El-Rahman, General formula of linear mixed integral equation with weak singular kernel, IOSR Journal of Mathematics, 2016, 12(4), 31-38. doi: 10.9790/5728-1204023138 [16] A. M. A. El-Sayed, H. H. G. Hashem and Y. M. Y. Omar, Positive continuous solution of a quadratic integral equation of fractional orders, Math. Sci. Lett., 2013, 2(1), 19-27. DOI: 10.12785/msl/020103. [17] H. Fatahi, J. Saberi-Nadjafi and E. Shivanian, A new spectral meshless radial point interpolation(SMRPI) method for the two-dimensional Fredholm integral equations on general domains with error analysis, J. Comput. Appl. Math., 2016, 294, 196-209. DOI: 10.1016/j.cam.2015.08.018. [18] I. C. Gredshtein and I. M. Ryzhik, Integrals Tables, Summation, Series and Derivatives, Fizmatgiz, Moscow, 1971. [19] C. D. Green, Integral Equation Methods, Nelsson, New York, 1969. [20] M. S. Hashmi, N. Khan and S. Iqbal, Numerical solutions of weakly singular Volterra integral equations using the optimal homotopy asymptotic method, Comput. Math. Appl., 2012, 64(6), 1567-1574. DOI: 10.1016/j.camwa.2011.12.084. [21] M. G. Krein, On a method for the effective solution of the inverse boundary problem, Dokl. Acad. Nauk. Ussr., 1954, 94(6). [22] N. N. Lebedev, Special Functions and their Applications, Dover, New York, 1972. [23] S. Micula, On some iterative numerical methods for a Volterra functional integral equation of the second kind, J. of Fixed Point Theory Appl., 2017, 19(3), 1815-1824. DOI: 10.1007/s11784-016-0336-6. [24] S. Micula, An iterative numerical method for fredholm-volterra integral equations of the second kind, appl. math. Comput., 2015, 270(1), 935-942. DOI: 10.1016/j.amc.2015.08.110. [25] F. Mirzaee and E. Hadadiyan, Application of modified hat functions for solving nonlinear quadratic integral equations, Iran J. Numer. Anal. Opt., 2016, 6(2), 65-84. DOI: 10.22067/ijnao.v6i2.46565. [26] N. I. Muskhelishvili, Singular Integral Equations, Noordhoff, Leiden, 1953. [27] M. E. Nasr and M. A. Abdel-Aty, Analytical discussion for the mixed integral equations, J. of Fixed Point Theory Appl., 2018, 20(3), 1-19. DOI: 10.1007/s11784-018-0589-3. [28] M. E. Nasr and M. A. Abdel-Aty, A new techniques applied to Volterra–Fredholm integral equations with discontinuous kernel, J. of Computational Analysis and Appl., 2021, 29(1), 11-24. [29] A. Palamora, Product integration for Volterra integral equations of the second kind with weakly singular kernels, Math. Comp., 1996, 65(215), 1201-1212. [30] J. Saberi-Nadjafi and A. Ghorbani, He's homotopy perturbation method: an effective tool for solving nonlinear integral and integro-differential equations, Comput. Math. Appl., 2009, 58(11-12), 2379-2390. DOI: 10.1016/j.camwa.2009.03.032. [31] V. V. Ter-Avetisyan, On dual integral equations in the semiconservative case, Journal of Contemporary Mathematical Analysis, 2012, 47(2), 62-69. DOI: 10.3103/S1068362312020021. [32] S. Yüzbaşl, N. Şahin and M. Sezer, Bessel polynomial solutions of high-order linear Volterra integro-differential equations, Comput. Math. Appl., 2011, 62(4), 1940-1956. DOI: 10.1016/j.camwa.2011.06.038. -
-
Figures(8) / Tables(2)
Export File
Citation
Mohammed Abdel-Aty, Mohammed Abdou. ANALYTICAL AND NUMERICAL DISCUSSION FOR THE PHASE-LAG VOLTERRA-FREDHOLM INTEGRAL EQUATION WITH SINGULAR KERNEL[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3203-3220. doi: 10.11948/20220547
Format
Content
DownLoad:
-
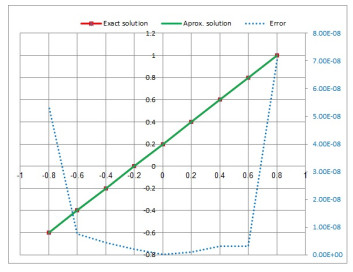
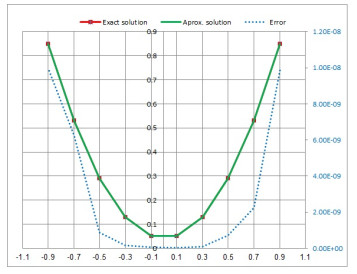
Figure 1.
Exact and approximate solution of Legendre polynomials for
$ t_{0}=0. $ -
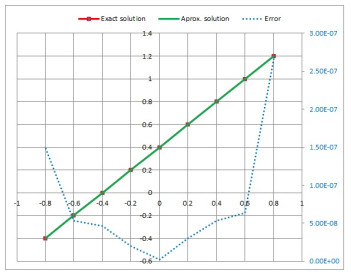
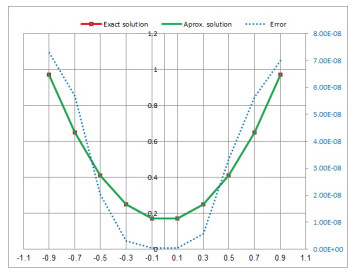
Figure 2.
Exact and approximate solution of Legendre polynomials for
$ t_{1}=0.2. $ -
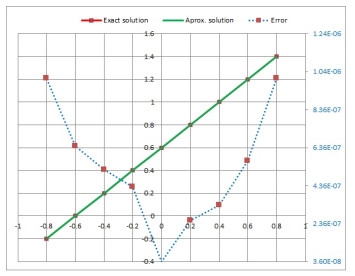
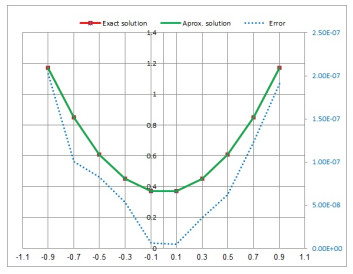
Figure 3.
Exact and approximate solution of Legendre polynomials for
$ t_{1}=0.4. $ -
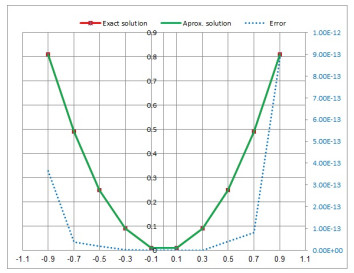
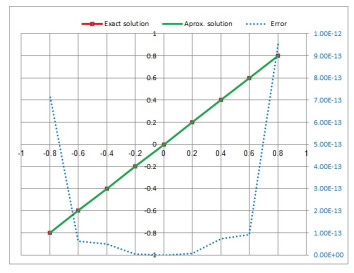
Figure 4.
Exact and approximate solution of Legendre polynomials for
$ t_{1}=0.6. $ -
Figure 5.
Exact and approximate solution of Legendre polynomials for
$ t_{0}=0. $ -
Figure 6.
Exact and approximate solution of Legendre polynomials for
$ t_{1}=0.2. $ -
Figure 7.
Exact and approximate solution of Legendre polynomials for
$ t_{1}=0.4. $ -
Figure 8.
Exact and approximate solution of Legendre polynomials for
$ t_{1}=0.6. $