| Citation: | Mahmoud S. Rawashdeh, Nazek A. Obeidat, Hala Abedalqader. NEW CLASS OF NONLINEAR FRACTIONAL INTEGRO-DIFFERENTIAL EQUATIONS WITH THEORETICAL ANALYSIS VIA FIXED POINT APPROACH: NUMERICAL AND EXACT SOLUTIONS[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2767-2787. doi: 10.11948/20220575 |
NEW CLASS OF NONLINEAR FRACTIONAL INTEGRO-DIFFERENTIAL EQUATIONS WITH THEORETICAL ANALYSIS VIA FIXED POINT APPROACH: NUMERICAL AND EXACT SOLUTIONS
-
Abstract
The analysis of fractional Integro-differential equations is valuable for researchers in the science community. For the present work, we examine the analysis of a newly technique called the Fractional Decomposition Method (FDM) via fixed point approach applies to nonlinear fractional Volterra Integro-Differential equations. Then, we implement the method on four test problems such as; Fractional Volterra Integro-Differential Equations (FVIDE). We present exact and approximate solutions to fractional Volterra Integro-Differential equations. The Caputo fractional derivative will be considered in the current work.
-

-
References
[1] T. A. Abassy, New treatment of Adomian decomposition method with compaction equations, Studies in Nonlinear Sciences, 2010, 1(2), 41–49. [2] G. Adomian, A review of the decomposition method in applied mathematics, Journal of mathematical analysis and applications, 1988, 135(2), 501–544. doi: 10.1016/0022-247X(88)90170-9 [3] A. Arikoglu and I. Ozkol, Solution of fractional integro-differential equations by using fractional differential transform method, Chaos, Solitons & Fractals, 2009, 40(2), 521–529. [4] B. Ahmad, J. Henderson and R. Luca, Boundary Value Problems for Fractional Differential Equations and Systems, 2021. [5] F. B. M. Belgacem and R. Silambarasan, Theory of natural transform, Math. Engg. Sci. Aeros., 2012, 3, 99–124. [6] H. Bulut, H. M. Baskonus and F. B. M. Belgacem, The analytical solution of some fractional ordinary differential equations by the Sumudu transform method, Abstract and Applied Analysis, Hindawi, 2013, 2013. [7] M. Caputo, Elasticita de dissipazione, Zanichelli, Bologna, Italy, (Links), SIAM journal on numerical analysis, 1969. [8] P. Darania and A. Ebadian, A method for the numerical solution of the integro-differential equation, Applied Mathematics and Computation, 2007, 188(1), 657–668. doi: 10.1016/j.amc.2006.10.046 [9] M. El-Shahed, Application of He's homotopy perturbation method to Volterra's integro-differential equation, International Journal of Nonlinear Sciences and Numerical Simulation, 2005, 6(2), 163–168. [10] L. Huang, X. Li, Y. Zhao and X. Duan, Approximate solution of fractional integro-differential equations by Taylor expansion method, Computers & Mathematics with Applications, 2011, 62(3), 1127–1134. doi: 10.3969/j.issn.1001-3695.2011.03.094 [11] R. E. Hilfer, Applications of fractional calculus in physics, World scientific, 2000. [12] A. A. Hamoud, M. S. Abdo and K. P. Ghadle, Existence and uniqueness results for Caputo fractional integro-differential equations, Journal of the Korean Society for Industrial and Applied Mathematics, 2018, 22(3), 163–177. [13] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and applications of fractional differential equations, Elsevier, 2006, 204. [14] D. Loonker and P. K. Banerji, Natural transform and solution of integral equations for distribution spaces, American Journal of Mathematics and Sciences, 2014, 3(1), 65–72. [15] K. S. Miller and B. Ross, An introduction to the fractional calculus and fractional differential equations, Wiley, 1993. [16] H. Mesgarani, H. Safdariı, A. Ghasemian and Y. Esmaeelzade, The Cubic B-spline Operational Matrix Based on Haar Scaling Functions for Solving Varieties of the Fractional Integro-differential Equations, Journal of Mathematics, 2019, 51(8), 45–65. [17] A. M. Mahdy and R. T. Shwayyea, Numerical solution of fractional integro-differential equations by least squares method and shifted Laguerre polynomials pseudo-spectral method, International Journal of Scientific & Engineering Research, 2016, 7(4), 1589–1596. [18] M. M. Miah, A. R. Seadawy, H. S. Ali and M. A. Akbar, Abundant closed form wave solutions to some nonlinear evolution equations in mathematical physics, Journal of Ocean Engineering and Science, 2020, 5(3), 269–278. doi: 10.1016/j.joes.2019.11.004 [19] D. Nazari and S. Shahmorad, Application of the fractional differential transform method to fractional-order integro-differential equations with nonlocal boundary conditions, Journal of Computational and Applied Mathematics, 2010, 234(3), 883–891. doi: 10.1016/j.cam.2010.01.053 [20] N. A. Obeidat and D. E. Bentil, New theories and applications of tempered fractional differential equations, Nonlinear Dynamics, 2021, 105(2), 1689–1702. doi: 10.1007/s11071-021-06628-4 [21] I. Podlubny, Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Elsevier, 1998. [22] M. S. Rawashdeh and H. Al-Jammal, New approximate solutions to fractional nonlinear systems of partial differential equations using the FNDM, Advances in Difference Equations, 2016, 1, 1–19. [23] M. S. Rawashdeh, The fractional natural decomposition method: theories and applications, Mathematical Methods in the Applied Sciences, 2017, 40(7), 2362–2376. doi: 10.1002/mma.4144 [24] N. H. Sweilam and M. Khader, A Chebyshev pseudo-spectral method for solving fractional-order integro-differential equations, The ANZIAM Journal, 2010, 51(4), 464–475. doi: 10.1017/S1446181110000830 [25] M. A. Shallal, K. K. Ali, K. R. Raslan, H. Rezazadeh and A. Bekir, Exact solutions of the conformable fractional EW and MEW equations by a new generalized expansion method, Journal of Ocean Engineering and Science, 2020, 5(3), 223–229. doi: 10.1016/j.joes.2019.12.004 [26] El-Kalla, I.L.; Convergence of Adomian's Method Applied to A Class of Volterra Type Integro-Differential Equations. International Journal of Differential Equations and Applications, 10(2), 225-234, (2005). -
-
-
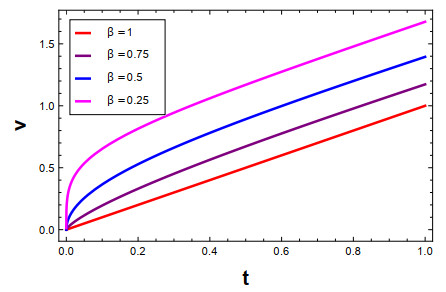
Figure 1.
Numerical values for
$ v\left(t\right) $ $ \beta $ $ 0\le t\le 1 $ -
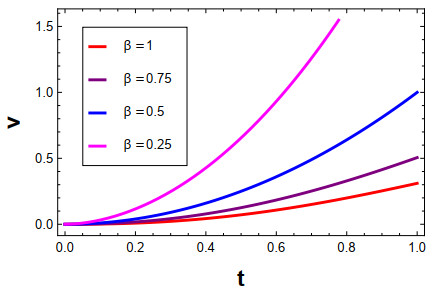
Figure 2.
Numerical Solutions of
$ v\left(t\right) $ $ \beta $ $ 0\le t\le 1 $




 DownLoad:
DownLoad: