| Citation: | Weili Liu, Hongpeng Zhang, Weipeng Zhang, Xuenan Sun. DYNAMICAL BEHAVIORS OF A TUMOR-IMMUNE-VITAMIN MODEL WITH RANDOM PERTURBATION[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2739-2766. doi: 10.11948/20220558 |
DYNAMICAL BEHAVIORS OF A TUMOR-IMMUNE-VITAMIN MODEL WITH RANDOM PERTURBATION
-
Abstract
This paper mainly explores the stochastic behaviors of the interaction between tumor cells and immune cells when vitamins are added. First, it is shown that the stochastic tumor-immune-vitamin model has a unique global positive solution. Second, we obtain that the solution of our model is stochastically ultimately bounded, stochastically permanent, extinct and persistent in mean under some threshold conditions. Moreover, when the perturbation is weak, the stochastic model has a unique stationary distribution. Finally, numerical simulations are performed to verify the theoretical results.
-
Keywords:
- Tumor-immune-vitamin model /
- stochastic process /
- extinction /
- persistence /
- stationary distribution
-

-
References
[1] R. Aboulaich, A. Darouichi, I. Elmouki and A. Jraifi, A stochastic optimal control model for BCG immunotherapy in superficial bladder cancer, Math. Model. Nat. Phenom., 2017, 12(5), 99–119. doi: 10.1051/mmnp/201712507 [2] S. A. Alharbi and A. S. Rambely, Dynamic behaviour and stabilisation to boost the immune system by complex interaction between tumour cells and vitamins intervention, Adv. Difference Equ., 2020, 412. DOI: 10.1186/s13662-020-02869-6. [3] J. Bao and J. Shao, Permanence and extinction of regime-switching predator-prey models, SIAM J. Math. Anal., 2016, 48(1), 725–739. doi: 10.1137/15M1024512 [4] V. I. Bogachev, N. V. Krylov and M. Röckner, On regularity of transition probabilities and invariant measures of singular diffusions under minimal conditions, Comm. Partial Differential Equations, 2001, 26(11–12), 2037–2080. doi: 10.1081/PDE-100107815 [5] L. Chen and J. Chen, Nonlinear Biological Dynamical System, Science Press, Beijing, 1993. [6] N. T. Dieu, D. H. Nguyen, N. Du and G. Yin, Classification of asymptotic behavior in a stochastic SIR model, SIAM J. Appl. Dyn. Syst., 2016, 15(2), 1062–1084. doi: 10.1137/15M1043315 [7] Y. Ding, G. Liu and Y. An, Stability and bifurcation analysis of a tumor-immune system with two delays and diffusion, Math. Biosci. Eng., 2022, 19(2), 1154–1173. [8] N. Du, D. H. Nguyen and G. Yin, Conditions for permanence and ergodicity of certain stochastic predator-prey models, J. Appl. Probab., 2016, 53(1), 187–202. doi: 10.1017/jpr.2015.18 [9] A. Gerisch, R. Penta and J. Lang, Multiscale models in mechano and tumor biology, Springer, Cham., Switzerland, 2017. [10] W. Guo and D. Mei, Stochastic resonance in a tumor-immune system subject to bounded noises and time delay, Phys. A., 2014, 416, 90–98. doi: 10.1016/j.physa.2014.08.003 [11] D. J. Higham, An algorithmic introduction to numerical simulation of stochastic differential equations, SIAM Rev., 2001, 43(3), 525–546. doi: 10.1137/S0036144500378302 [12] Y. J. Hong, J. Kim, H. Y. Lee and C. H. Rim, Development of the anti-cancer food scoring system 2.0: validation and nutritional analyses of quantitative anti-cancer food scoring model, Nutr. Res. Pract., 2020, 14(1), 32–44. doi: 10.4162/nrp.2020.14.1.32 [13] D. Jafari, A. Esmaeilzadeh, M. Mohammadi-Kordkhayli and N. Rezaei, Vitamin c and the immune system, Springer, Cham., Switzerland, 2019. [14] H. Khan, F. Hussain and A. Samad, Cure and prevention of diseases with vitamin c into perspective: an overview, J. Crit. Rev., 2020, 7(4), 289–293. [15] D. Kirschner and J. C. Panetta, Modeling immunotherapy of the tumor-immune interaction, J. Math. Biol., 1998, 37(3), 235–252. doi: 10.1007/s002850050127 [16] M. Krstić, On stability of stochastic delay model for tumor-immune interaction, Filomat, 2018, 32(4), 1273–1283. doi: 10.2298/FIL1804273K [17] V. A. Kuznetsov, L. A. Makalkin, M. A. Taylor and A. S. Perelson, Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis, Bull. Math. Biol., 1994, 56(2), 295–321. doi: 10.1007/BF02460644 [18] J. Li, X. Xie, Y. Chen and D. Zhang, Complex dynamics of a tumor-immune system with antigenicity, Appl. Math. Comput., 2021, 400, 126052. [19] D. Li and F. Cheng, The extinction and persistence of tumor evolution influenced by external fluctuations and periodic treatment, Qual. Theory Dyn. Syst., 2019, 18(3), 873–886. doi: 10.1007/s12346-019-00317-9 [20] D. Li and Y. Zhao, Survival analysis for tumor cells in stochastic switching environment, Appl. Math. Comput., 2019, 357, 199–205. [21] X. Li, G. Song, Y. Xia and C. Yuan, Dynamical behaviors of the tumor-immune system in a stochastic environment, SIAM J. Appl. Math., 2019, 79(6), 2193–2217. doi: 10.1137/19M1243580 [22] M. Liu and M. Deng, Permanence and extinction of a stochastic hybrid model for tumor growth, Appl. Math. Lett., 2019, 94, 66–72. doi: 10.1016/j.aml.2019.02.016 [23] K. J. Mahasa, R. Ouifki, A. L. Eladdadi and L. Pillis, Mathematical model of tumor-immune surveillance, J. Theoret. Biol., 2016, 404, 312–330. doi: 10.1016/j.jtbi.2016.06.012 [24] X. Mao, Stochastic differential equations and applications, Second Edition, Horwood Publishing, Chichester, 2008. [25] X. Mao and C. Yuan, Stochastic Differential Equations with Markovian Switching, Imperial College Press, London, 2006. [26] M. R. Owen and J. A. Sherratt, Modelling the macrophage invasion of tumors: effects on growth and composition, IMA J. Math. Appl. Med. Biol., 1998, 15(2), 165–185. doi: 10.1093/imammb/15.2.165 [27] L. Pillis, A. E. Radunskaya and C. L. Wiseman, A validated mathematical model of cell-mediated immune response to tumor growth, Cancer Res., 2005, 65(17), 7950–7958. doi: 10.1158/0008-5472.CAN-05-0564 [28] M. Rajalakshmi and M. Ghosh, Modeling treatment of cancer using virotherapy with generalized logistic growth of tumor cells, Stoch. Anal. Appl., 2018, 36(6), 1068–1086. doi: 10.1080/07362994.2018.1535319 [29] T. Suzuki, Mathematical methods for cancer evolution, Springer, Singapore, 2017. [30] M. Villasana and A. Radunskaya, A delay differential equation model for tumor growth, J. Math. Biol., 2003, 47(3), 270–294. doi: 10.1007/s00285-003-0211-0 [31] P. Wang, B. Li and Y. Li, Asymptotic behavior of a stochastic two-species competition system with impulsive effects, Int. J. Nonlinear Sci. Numer. Simul., 2018, 19(5), 427–438. doi: 10.1515/ijnsns-2015-0141 [32] J. Wu, D. H. Kirn and L. M. Wein, Analysis of a three-way race between tumor growth, a replication-competent virus and an immune response, Bull. Math. Biol., 2004, 66(4), 605–625. doi: 10.1016/j.bulm.2003.08.016 -
-
-
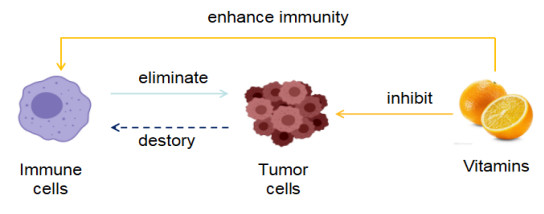
Figure 1.
The process of vitamins assisting immunotherapy.
-
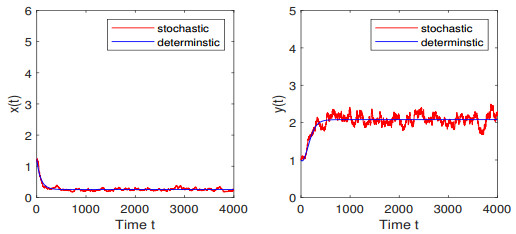
Figure 2.
The path of
$ x(t) $ $ y(t) $ -
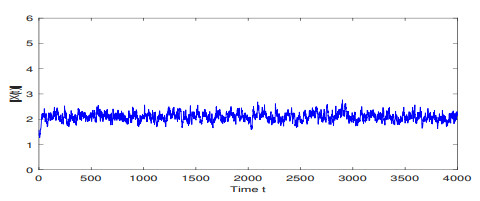
Figure 3.
The path of
$ |X(t)| $ $ X(t)=(x(t),y(t)) $ -
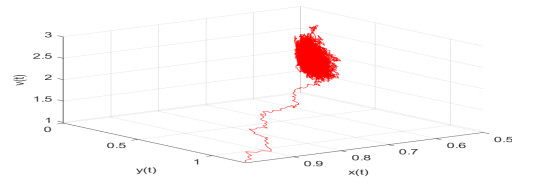
Figure 4.
The path of
$ (x(t),y(t),v(t)) $ -
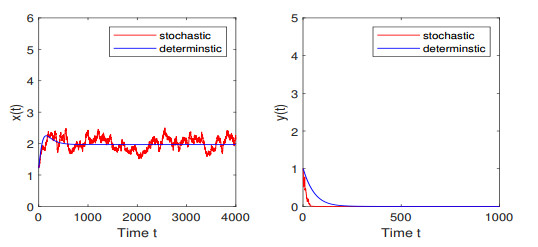
Figure 5.
The path of
$ x(t) $ $ y(t) $ -
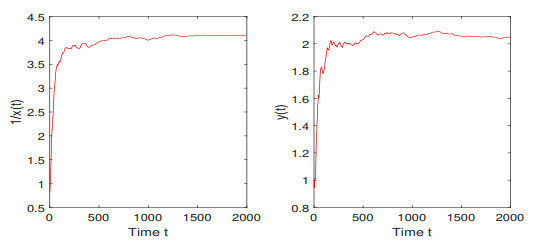
Figure 6.
The path of the time mean of
$ 1/x(t) $ $ y(t) $ -
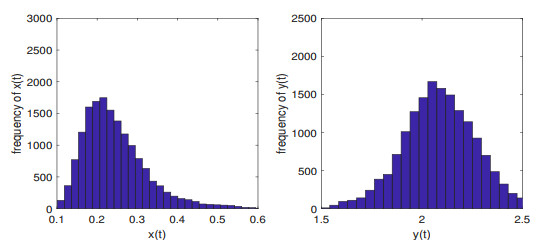
Figure 7.
Frequency histograms of
$ x(t) $ $ y(t) $




 DownLoad:
DownLoad: