| Citation: |
Hefei Zhao, Kuilin Wu. LIMIT CYCLES FOR PIECEWISE LINEAR SYSTEMS WITH IMPROPER NODE[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2720-2738. doi: 10.11948/20220555
|
LIMIT CYCLES FOR PIECEWISE LINEAR SYSTEMS WITH IMPROPER NODE
-
Abstract
This paper is concerned with the number of limit cycles of planar piecewise linear systems for improper node-improper node and improper node-node types with a straight line of separation. We obtain some sufficient conditions for the existence and stability of limit cycles and prove that the systems have at least two nested limit cycles in some parameter regions.
-
Keywords:
- Limit cycle /
- piecewise linear system /
- improper node
-
-
References
[1] A. Andronov, A. Vitt and S. Khaikin, Theory of Osillations, Pergamon Press, Oxford, 1966. [2] C. A. Buzzi, J. C. R. Medrado and F. Torres, Generic bifurcation of refracted systems, Adv. Math., 2013, 234, 653–666. doi: 10.1016/j.aim.2012.11.008 [3] M. di Bernardo, C. J. Budd, A. R. Champneys and P. Kowalczyk, Piecewise-smooth dynamical systems: Theory and applications, Springer, London, 2008. [4] A. F. Filippov, Differential equations with discontinuous righthand, Springer, London, 1988. [5] E. Freire, E. Ponce, F. Rodrigo and F. Torres, Bifurcation sets of continuous piecewise linear systems with two zones, Internat. J. Bifur. Chaos, 1998, 8(11), 2073–2097. doi: 10.1142/S0218127498001728 [6] E. Freire, E. Ponce and F. Torres, Canonical discontinuous planar piecewise linear systems, SIAM J. Appl. Dyn. Syst., 2012, 11(1), 181–211. doi: 10.1137/11083928X [7] E. Freire, E. Ponce and F. Torres, A general mechanism to generate three limit cycles in planar Filippov systems with two zones, Nonlin. Dynam., 2014, 78(1), 251–263. doi: 10.1007/s11071-014-1437-7 [8] F. Giannakopoulos and K. Pliete, Planar systems of piecewise linear differential equations with a line of discontinuity, Nonlinearity, 2001, 14(6), 1611–1632. doi: 10.1088/0951-7715/14/6/311 [9] M. Han and W. Zhang, On Hopf bifurcation in non-smooth planar systems, J. Diff. Eqs., 2010, 248(9), 2399–2416. doi: 10.1016/j.jde.2009.10.002 [10] S. Huan and X. Yang, On the number of limit cycles in general planar piecewise linear systems, Discrete Contin. Dyn. Syst., 2012, 32(6), 2147–2164. doi: 10.3934/dcds.2012.32.2147 [11] S. Huan and X. Yang, Existence of limit cycles in general planar piecewise linear systems of saddle-saddle dynamics, Nonlin. Anal., 2013, 92, 82–95. doi: 10.1016/j.na.2013.06.017 [12] S. Huan and X. Yang, On the number of limit cycles in general planar piecewise linear systems of node-node types, J. Math. Anal. Appl., 2014, 411(1), 340–353. doi: 10.1016/j.jmaa.2013.08.064 [13] W. Hou and S. Liu, Melnikov functions for a class of piecewise Hamiltonian system, J Nonlin. Model Anal., 2023, 5(1), 123–145. [14] G. A. Kriegsmann, The rapid bifurcation of the Wien bridge oscillator, IEEE Trans. Circuits Syst., 1987, 34(9), 1093–1096. doi: 10.1109/TCS.1987.1086245 [15] R. Lum and L. O. Chua, Global properties of continuous piecewise linear vector fields. Part Ⅰ: Simplest case in $\mathbb{R}^2$, Internat. J. Circuit Theor. Appl., 1991, 19(3), 251–307. doi: 10.1002/cta.4490190305 [16] J. Llibre and E. Ponce, Three nested limit cycles in discontinous piecewise linear differential systems with two zones, Discrete Contin. Dyn. Syst. Ser. B, 2012, 19(3), 325–335. [17] J. Llibre and X. Zhang, Limit cycles for discontinuous planar piecewise linear differential systems separated by one straight line and having a center, J. Math. Anal. Appl., 2018, 467(1), 537–549. doi: 10.1016/j.jmaa.2018.07.024 [18] T. Li, H. Chen and X. Chen, Crossing periodic orbits of nonsmooth Liénard systems and applications, Nonlinearity, 2020, 33(11), 5817–5838. doi: 10.1088/1361-6544/ab9bac [19] T. Li and X. Chen, Periodic orbits of linear Filippov systems with a line of discontinuity, Qual. Theor. Dyn. Syst., 2020, 19(1), 1–22. doi: 10.1007/s12346-019-00337-5 [20] N. B. Pettit and P. E. Wellstead, Analyzing piecewise linear dynamical systems, IEEE Control Syst. Mag., 1995, 15(5), 43–50. doi: 10.1109/37.466263 [21] J. J. Stoker, Nonlinear vibrations in mechanical and electrical systems, Interscience, New York, 1950. [22] J. Wang, C. Huang and L. Huang, Discontinuity-induced limit cycles in a general planar piecewise linear system of saddle-focus type, Nonlin. Anal. Hybrid Syst., 2019, 33, 162–178. doi: 10.1016/j.nahs.2019.03.004 [23] J. Wang, X. Chen and L. Huang, The number and stability of limit cycles for planar piecewise linear systems of node-saddle type, J. Math. Anal. Appl., 2019, 469(1), 405–427. doi: 10.1016/j.jmaa.2018.09.024 [24] H. Zhao, K. Wu and Y. Shao, Global dynamics of a planar piececwise linear refracting system of node-node types, Internat. J. Bifur. Chaos, 2022, 32(13), 2250201. doi: 10.1142/S0218127422502017 -
-
Figures(3)
Export File
Citation
Hefei Zhao, Kuilin Wu. LIMIT CYCLES FOR PIECEWISE LINEAR SYSTEMS WITH IMPROPER NODE[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2720-2738. doi: 10.11948/20220555
Format
Content
DownLoad:
-
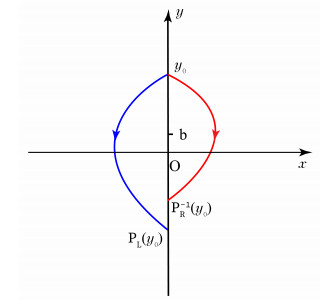
Figure 1.
Illustration of
$ P_L(y^-_0) $ $ P_R(y^+_0) $ $ b>0 $ -
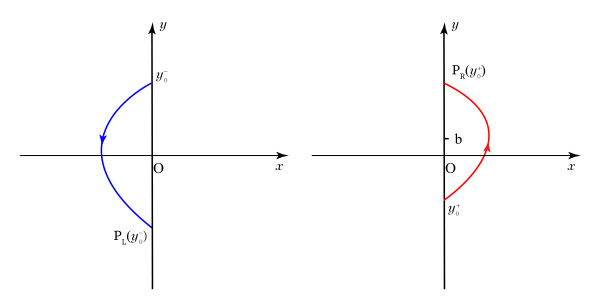
Figure 2.
Illustration of
$ \textbf{D}_1(y_{0};b) $ -
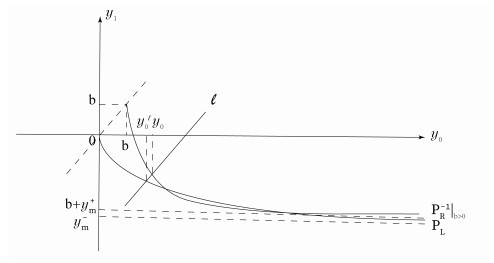
Figure 3.
Graphs of
$ P_L $ $ P_R^{-1}|_{b>0} $ $ y_m^- \leq y_m^+ + b <0 $ $ T^+ >0> T^- $ $ b \in (0, \; b_m) $