| Citation: | Jingnan Wang, Li Xu. OPTIMAL CONTROL OF TUMOR-LYMPHATIC MODEL WITH IMMUNO-CHEMOTHERAPY[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2703-2719. doi: 10.11948/20220553 |
OPTIMAL CONTROL OF TUMOR-LYMPHATIC MODEL WITH IMMUNO-CHEMOTHERAPY
-
Abstract
To find optimal methods to inhibit tumors, we propose a tumor-lymphocyte immune optimal model with immuno-chemotherapy. Firstly, we investigate the therapeutic effects of high-dose single immunotherapy and high-dose single chemotherapy for tumor logistic growth, respectively. Furthermore, we apply the optimal control theory to investigate the optimal control problem of immuno-chemotherapy to eliminate tumors, maximize the remaining number of lymphocytes and minimize the cost caused by drugs over a finite time interval. The necessary and sufficient conditions for the existence of optimal control are also discussed. Finally, the numerical results indicate that the effect of immuno-chemotherapy with strong killing rate to tumors and weak killing rate to immune cells is the most effective strategy in inhibiting tumor growth.
-
Keywords:
- Tumor-lymphatic model /
- immuno-chemotherapy /
- optimal control /
- stability
-

-
References
[1] F. M. Burnet, The concept of immunological surveillance, Prog. Exp. Tumor Res, 1970, 13, 1–27. doi: 10.1159/000386035 [2] C. Campos, J. Cristiana and D. F. M. Torres, Numerical optimal control of HIV transmission in Octave/Matlab, Math. Comput. Appl., 2019, 25(1), 1–20. [3] Y. Chen and X. Lai, Modeling the effect of gut microbiome on therapeutic efficacy of immune checkpoint inhibitors against cancer, Math. Biosic., 2022, 350, 108868. doi: 10.1016/j.mbs.2022.108868 [4] L. G. De Pillis and A. E. Radunskaya, A mathematical tumor model with immune resistance and drug therapy: an optimal control approach, Comput. Math. Method M., 2001, 3(2), 79–100. [5] P. Das, S. Das, P. Das, et al., Optimal control strategy for cancer remission using combinatorial therapy: a mathematical model-based approach, Chaos Soliton Fract., 2021, 145, 110789. doi: 10.1016/j.chaos.2021.110789 [6] L. G. De Pillis, W. Gu and A. E. Radunskaya, Mixed immunotherapy and chemotherapy of tumors: modeling, applications and biological interpretations, J. Theor. Biol., 2006, 238(4), 841–862. doi: 10.1016/j.jtbi.2005.06.037 [7] W. H. Fleming and R. W. Rishel, Deterministic and Stochastic Optimal Control, Springer-Verlag, New York, 1975. [8] M. Grapin, C. Richard, E. Limagne, et al., Optimized fractionated radiotherapy with anti-PD-L1 and anti-TIGIT: a promising new combination, J. Immunother. Cancer, 2019, 7(1), 1–12. doi: 10.1186/s40425-018-0484-x [9] A. Hoos, Evolution of end points for cancer immunotherapy trials, Annals of Oncology, 2012, 23(8), 47–52. [10] V. A. Kuznetsov, I. A. Makalkin, M. A. Taylor, et al., Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis, Bull. Math. Biol., 1994, 56(2), 295–321. doi: 10.1007/BF02460644 [11] A. K. Laird, Dynamics of tumor growth, Brit. J. Cancer, 1964, 13(3), 490–502. [12] D. L. Lukes, Differential Equations: Classical to Controlled, Academic Press, New York, 1982. [13] J. Lackie, A Dictionary of Biomedicine, Oxford University Press, Oxford, 2010. [14] S. Lenhart and J. T. Workman, Optimal Control Applied to Biological Models, Chapman and Hall/CRC, London, 2007. [15] R. Martin and K. L. Teo, Optimal Control of Drug Administration in Cancer Chemotherapy, World Scientific, Singapore, 1993. [16] H. Neves and H. F. Kwok, Recent advances in the field of anti-cancer immunotherapy, BBA Clinical, 2015, 3, 280–288. doi: 10.1016/j.bbacli.2015.04.001 [17] L. Pang, Z. Zhao and X. Song, Cost-effectiveness analysis of optimal strategy for tumor treatment, Chaos Soliton Fract., 2016, 87, 293–301. doi: 10.1016/j.chaos.2016.03.032 [18] L. Pang, S. Liu, X. Zhang, et al., Mathematical modeling and dynamic analysis of anti-tumor immune response, J. Appl. Math. Comput., 2020, 62(1–2), 473–488. doi: 10.1007/s12190-019-01292-9 [19] L. S. Potryagin, The Mathematical Theory of Optimal Processes, CRC Press, New York, 1987, 17–21. [20] F. A. Rihan, S. Lakshmanan and H. Maurer, Optimal control of tumour-immune model with time-delay and immuno-chemotherapy, Appl. Math. Comput., 2019, 353, 147–165. [21] G. W. Swan, Role of optimal control theory in cancer chemotherapy, Math. Biosci., 1990, 101(2), 237–284. [22] Y. Wang, J. Tian and J. Wei, Lytic cycle: a defining process in oncolytic virotherapy, Appl. Math. Model., 2013, 37, 5962–5978. [23] J. Wang and Y. Zhang, Dynamics of immunotherapy antitumor models with impulsive control strategy, Math. Meth. Appl. Sci., 2022, 45, 483–499. [24] H. Zhang and J. Chen, Current status and future directions of cancer immunotherapy, J. Cancer, 2018, 9(10), 1773–1781. -
-
-
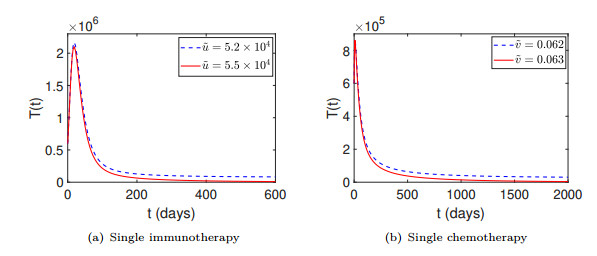
Figure 1.
The variations of the number of tumors with time for single therapy.
-
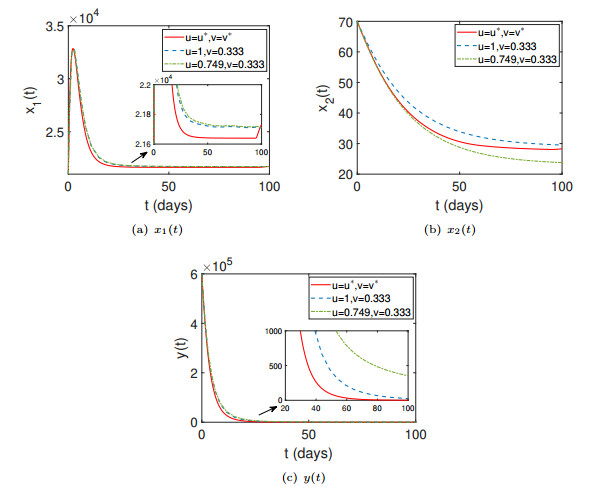
Figure 2.
Time series plots of optimal states and optimal control variables of the optimality system for different therapeutic strategies.
-
Figure 3.
Efficacy of immuno-chemotherapy for different drug doses.
-
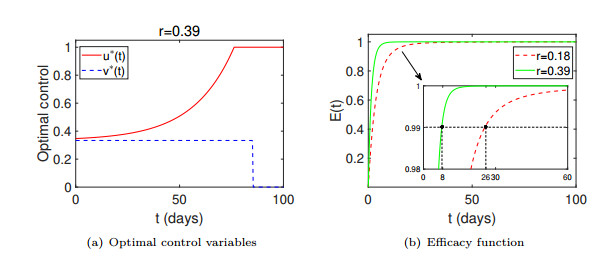
Figure 4.
Time series plots of optimal control variables and efficacy function for the optimal immuno-chemotherapy.




 DownLoad:
DownLoad: