| Citation: |
Jingnan Wang, Lu Zang, Li Xu. HOPF BIFURCATION AND CHAOS OF COMBINATIONAL IMMUNE ANTI-TUMOR MODEL WITH DOUBLE DELAYS[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2682-2702. doi: 10.11948/20220534
|
HOPF BIFURCATION AND CHAOS OF COMBINATIONAL IMMUNE ANTI-TUMOR MODEL WITH DOUBLE DELAYS
-
Abstract
In order to investigate the relations between tumor species growth and T cell activation assisted by dendritic cells, we establish a combinational immune anti-tumor model with double delays. Taking the activation rate of T cell and two time delays of tumor species growth and dendritic cell activation as parameters, we investigate the dynamical properties of the double delayed model, including the stability switches and the Hopf bifurcations of tumor-escape equilibrium and tumor-present equilibrium. With Hopf bifurcation curves, the center manifold theory and the normal form method, we find bi-stability states, the coexistence of two periodic solutions with different stabilities, two double Hopf bifurcation points, and use numerical simulations to show rich dynamic behaviors around the double Hopf bifurcation points, including the phase portraits and the corresponding Poincaré maps of chaotic attractors, as well as the progress transmission of unstable-oscillation-stable-oscillation. The theoretical and numerical results reveal the new methods of controlling tumor cells.
-
Keywords:
- Tumor-immune model /
- double time delays /
- chaotic attractor /
- stability switch /
- Hopf bifurcation
-
-
References
[1] Q. An, E. Beretta, Y. Kuang, et al., Geometric stability swith criteria in delay differential equations with two delays and delay dependent parameters, J. Differ. Equ., 2019, 266(11), 7073–7100. doi: 10.1016/j.jde.2018.11.025 [2] P. Bi, S. Ruan and X. Zhang, Periodic and chaotic oscillations in a tumor and immune system interaction model with three delays, Chaos, 2014, 24(2), 023101. doi: 10.1063/1.4870363 [3] Y. Du, B. Niu and J. Wei, Two delays induce Hopf bifurcation and double Hopf bifurcation in a diffusive Leslie-Gower predator-prey system, Chaos, 2019, 29, 013101. doi: 10.1063/1.5078814 [4] J. Hale, Theory of Functional Differential Equations, Springer-Verlag, New York, 1977. [5] B. D. Hassard, N. D. Kazarinoff and Y. Wan, Theory and Applications of Hopf Bifurcation, Cambridge University Press, Cambridge, 1981. [6] Z. Jiang and Y. Guo, Hopf bifurcation and stability crossing curve in a planktonic resource-consumer system with double delays, Int. J. Bifurcation Chaos, 2020, 30(13), 2050190. doi: 10.1142/S0218127420501904 [7] V. A. Kuznetsov, I. A. Makalkin, M. A. Taylor, et al., Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis, Bull. Math. Biol., 1994, 56(2), 295–321. doi: 10.1007/BF02460644 [8] D. Kirschner and J. C. Panetta, Modeling immunotherapy of the tumor-immune interaction, J. Math. Biol., 1998, 37, 235–252. doi: 10.1007/s002850050127 [9] X. Lai, A. Stiff, M. Duggan, et al., Modeling combination therapy for breast cancer with bet and immune check inhibitors, P. Natl. Acad. Sci. USA, 2018, 115(21), 5534–5539. doi: 10.1073/pnas.1721559115 [10] Y. Liu and J. Wei, Bifurcation analysis in delayed Nicholson blowflies equation with delayed harvest, Nonlinear Dyn., 2021, 105, 1805–1819. doi: 10.1007/s11071-021-06651-5 [11] X. Lin and H. Wang, Stability analysis of delay differential equations with two discrete delays, Canad. Appl. Math. Quart., 2012, 20(4), 519–533. [12] M. Li and H. Shu, Multiple stable periodic oscillations in a mathematical model of CTL response to HTLV-I infection, Bull. Math. Biol., 2011, 73, 1774–1793. doi: 10.1007/s11538-010-9591-7 [13] K. Li and J. Wei, Stability and Hopf bifurcation analysis of a prey-predator system with two delays, Chaos Soliton Fract., 2009, 42(5), 2606–2613. doi: 10.1016/j.chaos.2009.04.001 [14] M. Nagata, Y. Furta, Y. Takeuchi, et al., Dynamical behavior of combinational immune boost against tumor, Jpn. J. Ind. Appl. Math., 2015, 32(3), 759–770. doi: 10.1007/s13160-015-0193-5 [15] B. Niu, Y. Guo and Y. Du, Hopf bifurcation induced by delay effect in diffusive tumor-immune system, Int. J. Bifurcat Chaos, 2018, 28(11), 1850136. doi: 10.1142/S0218127418501365 [16] S. Ruan, Nonlinear dynamics in tumor-immune system interaction models with delays, Discrete Cont. Dyn. B., 2021, 26(1), 541–602. [17] S. Ruan and J. Wei, On the zeros of a third degree exponential polynomial with applications to a delayed model for the control of testosterone secretion, IMA J. Math. Appl. Med. Biol., 2001, 18, 41–52. doi: 10.1093/imammb/18.1.41 [18] S. Ruan and J. Wei, On the zeros of transcendental functions with applications to stability of delay differential equations with two delays, Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal., 2003, 10, 863–874. [19] A. Rescigno and C. Delisi, Immune surveillance and neoplasia¡ªⅡ A two-stage mathematical model, Bull. Math. Biol., 1977, 39(4), 487–497. [20] H. Song, W. Jiang and S. Liu, Virus dynamics model with interacelluar delays and immune response, Math. Biosci. Eng., 2015, 12(1), 1–24. doi: 10.3934/mbe.2015.12.1 [21] Y. Shu, J. Huang, Y. Dong, et al., Mathematical modeling and bifurcation analysis of pro-and anti-tumor macrophages, Appl. Math. Model., 2020, 88, 758–773. doi: 10.1016/j.apm.2020.06.042 [22] H. Shu, W. Xu, X. Wang, et al., Complex dynamics in a delay differential equation with two delays in tick growth with diapause, J. Differ Equ., 2020, 269, 10937–10963. doi: 10.1016/j.jde.2020.07.029 [23] Z. Song and J. Xu, Stability switches and double Hopf bifurcation in a two-neural network system with multiple delays, Cogn. Neurodynamics, 2013, 7(6), 505–521. doi: 10.1007/s11571-013-9254-0 [24] Y. Tian and Y. Yuan, Effect of time delays in an HIV virotherapy model with nonlinear incidence, Proc. R. Soc. A., 2016, 472, 20150626. doi: 10.1098/rspa.2015.0626 [25] J. Wang, H. Shi, L. Xu, et al., Hopf bifurcation and chaos of tumor-Lymphatic model with two time delays, Chaos Soliton Fract., 2022, 157, 111922. doi: 10.1016/j.chaos.2022.111922 [26] J. Wang and W. Jiang, Hopf-zero bifurcation of a delayed predator-prey model with dormancy of predators, J. Appl Anal Comput., 2017, 7(3), 1515–1069. [27] J. Wang and S. Liu, Turing and Hopf bifurcation in a diffusive tumor-immunemodel, J. Nonlinear Moldeling Anal., 2021, 3(3), 477–493. [28] J. Wang and W. Jiang, Bifurcation and chaos of a delayed predator-prey model with dormancy of predators, Nonlinear Dyn., 2012, 69, 1541–1558. doi: 10.1007/s11071-012-0368-4 [29] Y. Yuan and J. B$\acute{e}$lair, Threshold dynamics in an SEIRS model with latency and temporary immunity, J. Math. Biol., 2014, 69, 875–904. doi: 10.1007/s00285-013-0720-4 -
-
Figures(12) / Tables(5)
Export File
Citation
Jingnan Wang, Lu Zang, Li Xu. HOPF BIFURCATION AND CHAOS OF COMBINATIONAL IMMUNE ANTI-TUMOR MODEL WITH DOUBLE DELAYS[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2682-2702. doi: 10.11948/20220534
Format
Content
DownLoad:
-
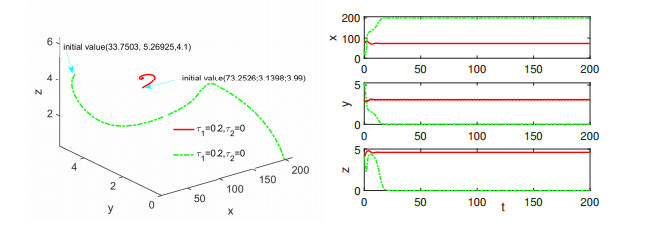
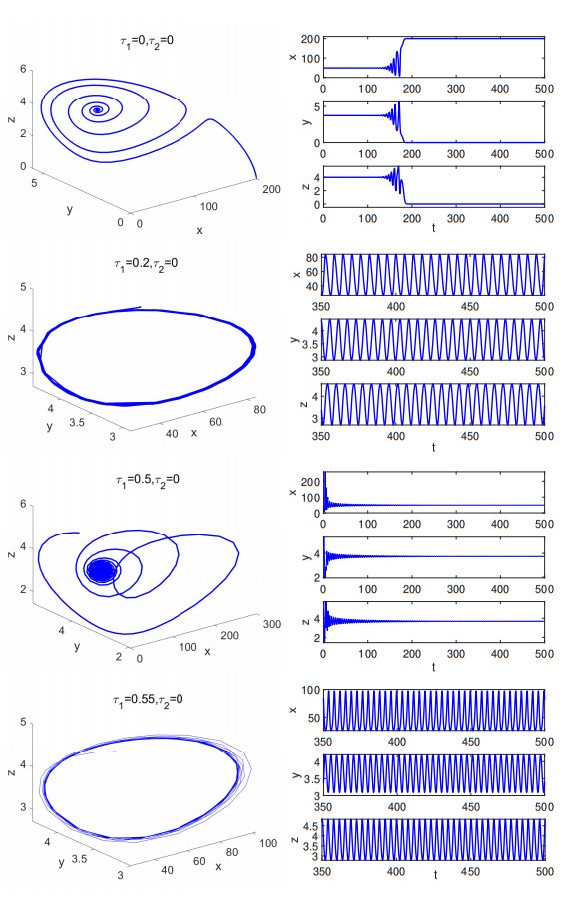
Figure 1.
The phase plane and solution curves of model (1.5) with
$ \tau_1=0 $ -
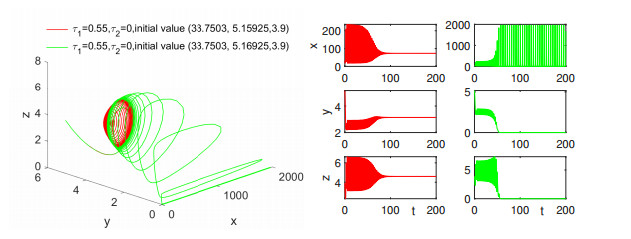
Figure 2.
The phase plane and solution curves of model (1.5) with
$ \tau_1=0.2, \tau_2=0 $ -
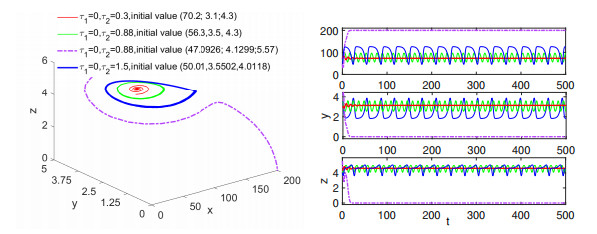
Figure 3.
An unstable periodic oscillation and a stable periodic oscillation of model (1.5).
-
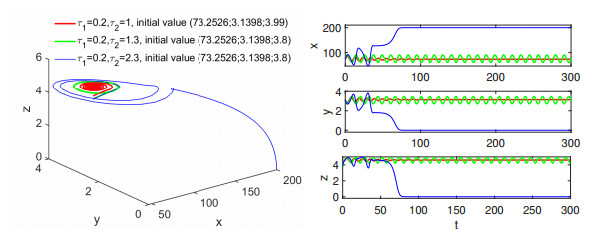
Figure 4.
The phase plane and solution curves of model (1.5) with
$ \tau_1=0.2 $ -
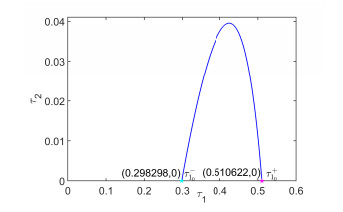
Figure 5.
The stability switch curves on
$ \tau_{1} $ $ \tau_{2} $ -
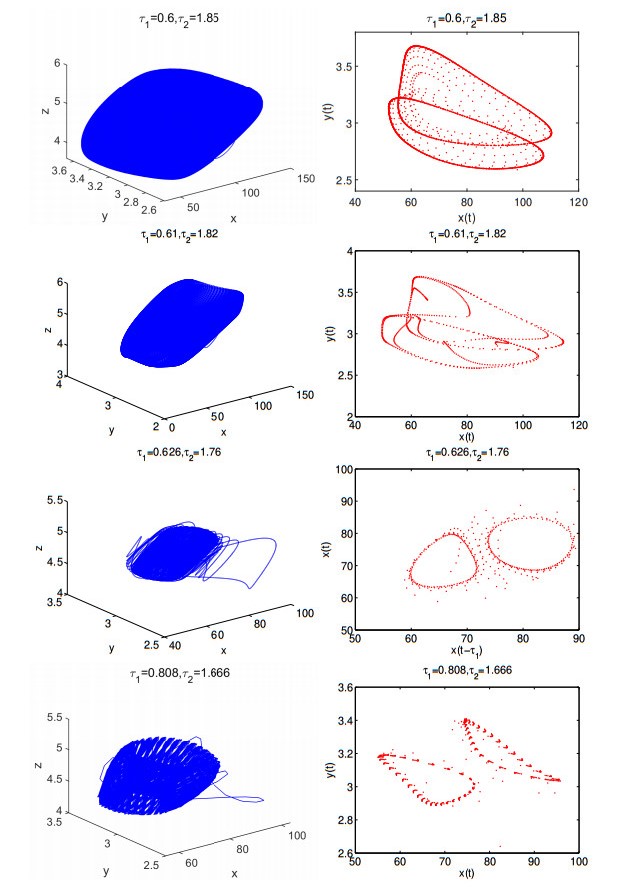
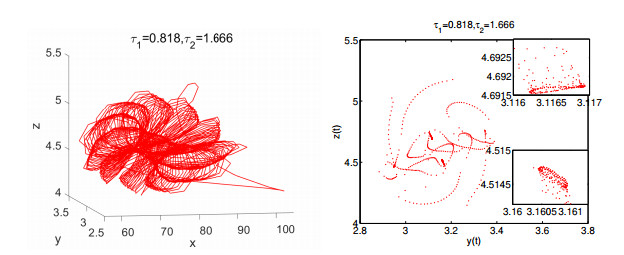
Figure 6.
The phase portraits of chaotic attractors of model (1.5), and the corresponding Poincar
$ \acute{e} $ $ \acute{e} $ $ z(t)=z* $ -
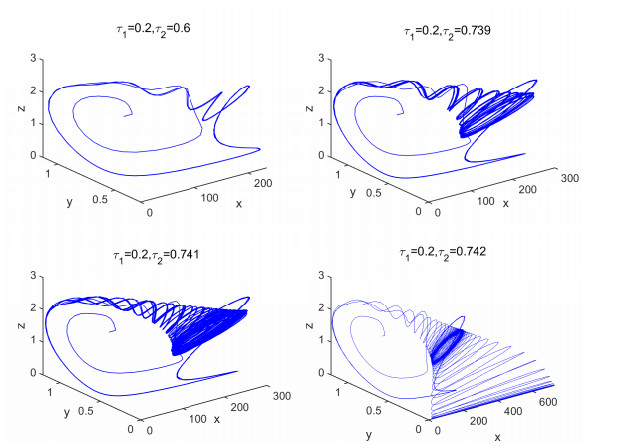
Figure 7.
The phase portraits of chaotic attractors of model (1.5), and the corresponding Poincar
$ \acute{e} $ $ \acute{e} $ $ x(t)=x* $ -
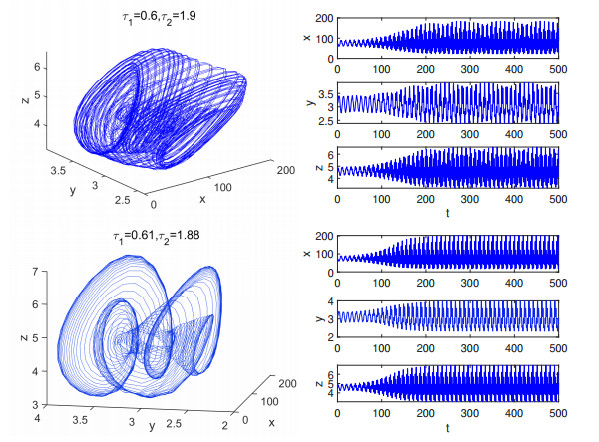
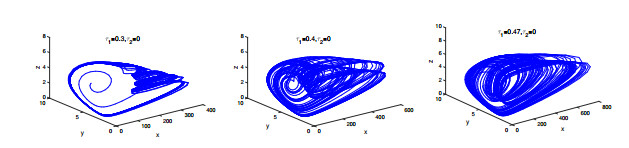
Figure 8.
Chaotic attractors of model (1.5) with coefficient condition (3.1)
-
Figure 9.
The stability switch curves on
$ \tau_{1} $ $ \tau_{2} $ $ b=0.25 $ -
Figure 10.
The phase plane and solution curves of model (1.5) with
$ b=0.25 $ -
Figure 11.
The phase diagrams of the chaos in model (1.5) with
$ K=260, \; a=0.02, \; b=0.25, \; c=1.2, \; r=6.2, \; \beta=1, \; \delta=0.9 $ -
Figure 12.
The phase diagrams of model (1.5) with
$ K=250, \; a=0.2, \; b=0.6, \; c=10, \; r=10, \; \beta=5, \; \delta=1 $