| Citation: | Lingling Liu, Ke-wei Ding, Zhiheng Yu. DYNAMICS OF A TWO-PREY AND ONE PREDATOR SYSTEM WITH QUADRATIC SELF INTERACTION[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2670-2681. doi: 10.11948/20220524 |
DYNAMICS OF A TWO-PREY AND ONE PREDATOR SYSTEM WITH QUADRATIC SELF INTERACTION
-
Abstract
A two-prey and one-predator system with quadratic self-interaction is discussed on subsets of special biological sense, none of which is closed under operations of the polynomial ring. The known work studied the stability of the boundary equilibria and gave invariant algebraic surfaces up to degree two but no further discussion for bifurcations. In this paper, we investigate the finite and infinite equilibria and their qualitative properties in the first octant. Moreover, we discuss their bifurcations, such as transcritical bifurcation on boundary equilibria, and give the bifurcation diagram. Finally, simulation examples are given to illustrate the theoretical results in this paper.
-
Keywords:
- Coexistence /
- stability /
- saddle-node /
- transcritical bifurcation
-

-
References
[1] I. K. Aybar, O. O. Aybar, M. Dukarić and B. Ferčec, Dynamical analysis of a two prey-one predator system with quadratic self interaction, Appl. Math. & Comput., 2018, 333, 118–132. [2] W. Aziz, Integrability and linearizability problems of three dimensional Lotka-Volterra equations of rank-2, Qual. Theory Dyn. Syst., 2019, 18, 1113–1134. doi: 10.1007/s12346-019-00329-5 [3] T. Bountis, Z. Zhunussova, K. Dosmagulova and G. Kanellopoulos, Integrable and non-integrable Lotka-Volterra systems, Phys. Lett. A, 2021, 402, article number: 127360. [4] J. Carr, Applications of Centre Manifold Theory, Springer, New York, 1981. [5] H. Chen and C. Zhang, Analysis of the dynamics of a predator-prey model with Holling functional response, J. Nonlinear Model. Anal., 2022, 4(2), 310–324. [6] A. Cima and J. Llibre, Bounded polynomial vector fields, Trans. Amer. Math. Soc., 1990, 318, 557–579. doi: 10.1090/S0002-9947-1990-0998352-5 [7] F. Gantmacher, The Theory of Matrices, Chelsea, New York, 1959. [8] P. Gatabazi, J. C. Mba, E. Pindza and C. Labuschagne, Grey Lotka-Volterra models with application to cryptocurrencies adoption, Chaos, Solitons & Fractals, 2019, 122, 47–57. [9] J. K. Hale, Ordinary Differential Equations, Wiley Interscience, New York, 1980. [10] S. B. Hsu, S. P. Hubbell and P. Waltman, Competing predators, SIAM J. Appl. Math., 1978, 35, 617–625. doi: 10.1137/0135051 [11] J. P. Keener, Oscillatory coexistence in the chemostat: A codimension two unfolding, SIAM J. Appl. Math., 1983, 43, 1005–1018. doi: 10.1137/0143066 [12] Y. Kuang, T. W. Hwang and S. B. Hsu, Global dynamics of a predator-prey model with Hassell-varley type functional response, Discrete Contin. Dyn. Syst. Ser. B, 2012, 10(4), 857–871. [13] J. Llibre and D. Xiao, Global dynamics of a lotka-volterra model with two predators competing for one prey, SIAM J. Appl. Math., 2014, 74(2), 434–453. doi: 10.1137/130923907 [14] J. L. Mata-Machuca, R. M. Martšªnez-Guerra and R. Aguilar-López, Monitoring in a predator-prey systems via a class of high order observer design, Biosystems, 2010, 100(1), 65–69. doi: 10.1016/j.biosystems.2010.01.003 [15] H. L. Smith, The interaction of steady state and Hopf bifurcations in a two-predator-one-prey competition model, SIAM J. Appl. Math., 1982, 42, 27–43. doi: 10.1137/0142003 [16] Y. Yao and L. Liu, Dynamics of a Leslie-Gower predator-prey system with hunting cooperation and prey harvesting, Discrete Contin. Dyn. Syst. Ser. B, 2022, 27(9), 4787–4815. doi: 10.3934/dcdsb.2021252 [17] Y. Zhu, S. Li and Y. Dai, Stability analysis of a fractional predator-prey system with two delays and incommensurate orders, J. Appl. Anal. Comput., 2022, 12(3), 981–1006. -
-
-
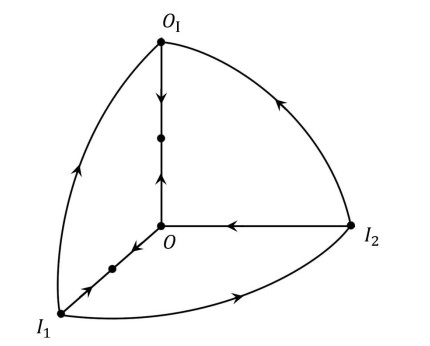
Figure 1.
The phase portraits of system (2.1) near all equilibria at infinity on
$ S^2 $ -
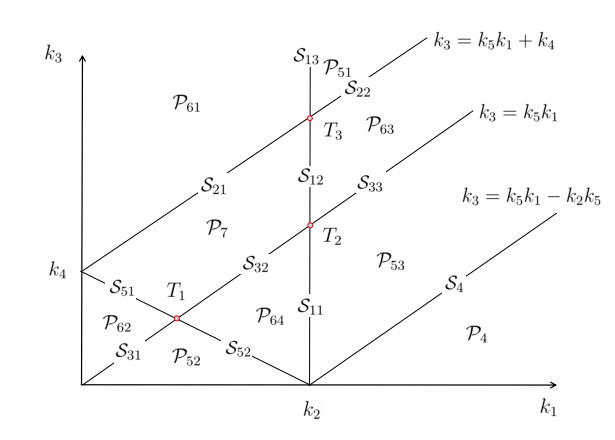
Figure 2.
Bifurcation diagram on
$ k_1k_3 $ -
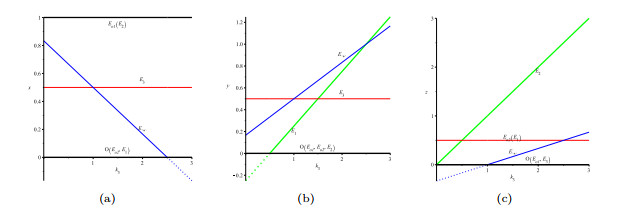
Figure 3.
Bifurcation diagram of system (2.1) for
$ k_1=0.5, k_2=1, k_4=2, k_5=1 $




 DownLoad:
DownLoad: