| Citation: |
Jiaopeng Yang, Pengxian Zhu. A NOVEL 5D SYSTEM GENERATED INFINITELY MANY HYPERCHAOTIC ATTRACTORS WITH THREE POSITIVE LYAPUNOV EXPONENTS[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2843-2873. doi: 10.11948/20230016
|
A NOVEL 5D SYSTEM GENERATED INFINITELY MANY HYPERCHAOTIC ATTRACTORS WITH THREE POSITIVE LYAPUNOV EXPONENTS
-
Abstract
Little seems to be known about the five-dimensional (5D) differential dynamical system with infinitely many hyperchaotic attractors, which have three positive Lyapunov exponents under no or infinitely many equilibria. This article presents a 5D dynamical system that can generate infinitely many hyperchaotic attractors. Of particular interest is the system exists not only infinitely many hyperchaotic attractors but also infinitely many periodic attractors in the following three cases: (ⅰ) no equilibria, (ⅱ) only infinitely many non-hyperbolic equilibria, (ⅲ) only infinitely many hyperbolic equilibria. By numerical analysis, one finds the 5D system could generate infinitely many coexisting hyperchaotic or chaotic or periodic attractors in the three kinds of equilibria cases. And one obtains the global dynamical behavior of the system, such as the Lyapunov exponential spectrum, bifurcation diagram. To study the hyperchaotic complexity of the 5D system, we rigorously show the stability of hyperbolic equilibria and some mathematical characterization for 5D Hopf bifurcation. In particular, the existence of an infinite number of isolated bifurcated periodic orbits is strictly proven. These complex dynamics studies in this paper may further contribute to a deep understanding of the hyperchaotic systems with infinitely many attractors.
-
Keywords:
- Hyperchaos /
- multistability /
- equilibria and stability /
- coexisting attractors /
- Hopf bifurcation
-
-
References
[1] M. Abdul Rahim, H. Natiq, N. Fataf and S. Banerjee, Dynamics of a new hyperchaotic system and multistability, Eur. Phys. J. Plus, 2019, 134(10), 1–9. [2] G. Chen and T. Ueta, Yet another chaotic attractor, Int. J. Bifurcation Chaos, 1999, 9(07), 1465–1466. doi: 10.1142/S0218127499001024 [3] Y. Chen and Q. Yang, A new Lorenz-type hyperchaotic system with a curve of equilibria, Math. Comput. Simulat., 2015, 112, 40–55. doi: 10.1016/j.matcom.2014.11.006 [4] L. Chua, M. Komuro and T. Matsumoto, The double scroll family, IEEE Trans. Circuits Syst., 1986, 33(11), 1072–1118. doi: 10.1109/TCS.1986.1085869 [5] C. Fan and Q. Ding, A universal method for constructing non-degenerate hyperchaotic systems with any desired number of positive lyapunov exponents, Chaos Solitons & Fractals, 2022, 161, 112323. [6] S. Fathizadeh, S. Behnia, F. Nemati, et al., Chaotic control of the dynamical behavior of covid-19 through the electromagnetic fields, Phys. Scripta, 2022, 97(8), 085008. doi: 10.1088/1402-4896/ac7fc1 [7] B. D. Hassard, N. D. Kazarinoff and Y. Wan, Theory and Applications of Hopf Bifurcation, 41, Cambridge University Press, 1981. [8] M. W. Hirsch, S. Smale and R. L. Devaney, Differential Equations, Dynamical Systems, and An Introduction to Chaos, Academic Press, 2012. [9] G. Hu, Generating hyperchaotic attractors with three positive lyapunov exponents via state feedback control, Int. J. Bifurcation Chaos, 2009, 19(02), 651–660. doi: 10.1142/S0218127409023275 [10] S. Jafari and J. C. Sprott, Simple chaotic flows with a line equilibrium, Chaos Solitons & Fractals, 2013, 57, 79–84. [11] H. Jahanshahi, A. Yousefpour, Z. Wei, et al., A financial hyperchaotic system with coexisting attractors: Dynamic investigation, entropy analysis, control and synchronization, Chaos Solitons & Fractals, 2019, 126, 66–77. [12] A. J. M. Khalaf, H. R. Abdolmohammadi, A. Ahmadi, et al., Extreme multi-stability analysis of a novel 5D chaotic system with hidden attractors, line equilibrium, permutation entropy and its secure communication scheme, Eur. Phys. J. Spec. Top., 2020, 229(6), 1175–1188. [13] G. A. Leonov, N. V. Kuznetsov and T. N. Mokaev, Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion, Eur. Phys. J. Spec. Top., 2015, 224(8), 1421–1458. doi: 10.1140/epjst/e2015-02470-3 [14] G. A. Leonov, N. V. Kuznetsov and V. I. Vagaitsev, Localization of hidden Chuaʼs attractors, Phys. Lett. A, 2011, 375(23), 2230–2233. doi: 10.1016/j.physleta.2011.04.037 [15] G. A. Leonov, N. V. Kuznetsov and V. I. Vagaitsev, Hidden attractor in smooth Chua systems, Physica D, 2012, 241(18), 1482–1486. doi: 10.1016/j.physd.2012.05.016 [16] H. Lin, C. Wang, Q. Deng, et al., Review on chaotic dynamics of memristive neuron and neural network, Nonlinear Dyn., 2021, 106(1), 959–973. doi: 10.1007/s11071-021-06853-x [17] E. N. Lorenz, Deterministic nonperiodic flow, J. Atmos. Sci., 1963, 20(2), 130–141. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [18] O. S. Ojoniyi and A. N. Njah, A 5D hyperchaotic sprott b system with coexisting hidden attractors, Chaos Solitons & Fractals, 2016, 87, 172–181. [19] A. Ouannas, A. Karouma, G. Grassi, et al., A novel secure communications scheme based on chaotic modulation, recursive encryption and chaotic masking, Alex. Eng. J., 2021, 60(1), 1873–1884. doi: 10.1016/j.aej.2020.11.035 [20] O. E. Rössler, An equation for continuous chaos, Phys. Lett. A, 1976, 57(5), 397–398. doi: 10.1016/0375-9601(76)90101-8 [21] C. Shen, S. Yu, J. Lü and G. Chen, A systematic methodology for constructing hyperchaotic systems with multiple positive lyapunov exponents and circuit implementation, IEEE Trans. Circuits Syst. I, 2013, 61(3), 854–864. [22] C. Shen, S. Yu, J. Lü and G. Chen, Designing hyperchaotic systems with any desired number of positive lyapunov exponents via a simple model, IEEE Trans. Circuits Syst. I, 2014, 61(8), 2380–2389. doi: 10.1109/TCSI.2014.2304655 [23] L. P. Shil'nikov, A. V. Shil'nikov, D. V. Turaev and L. O. Chua, Methods of Qualitative Theory in Nonlinear Dynamics (Part Ⅱ), 5, World Scientific, 2001. [24] J. P. Singh and B. K. Roy, Five new 4-D autonomous conservative chaotic systems with various type of non-hyperbolic and lines of equilibria, Chaos Solitons & Fractals, 2018, 114, 81–91. [25] J. C. Sprott, Some simple chaotic flows, Phys. Rev. E, 1994, 50(2), R647. doi: 10.1103/PhysRevE.50.R647 [26] P. Trikha and L. S. Jahanzaib, Dynamical analysis of a novel 5-d hyper-chaotic system with no equilibrium point and its application in secure communication. , Differ. Geom. Dyna. Syst., 2020, 22. [27] S. Vaidyanathan, V. T. Pham and C. K. Volos, A 5D hyperchaotic rikitake dynamo system with hidden attractors, Eur. Phys. J. Spec. Top., 2015, 224(8), 1575–1592. doi: 10.1140/epjst/e2015-02481-0 [28] Q. Wan, F. Li, Z. Yan, et al., Dynamic analysis and circuit realization of a novel variable-wing 5D memristive hyperchaotic system with line equilibrium, Eur. Phys. J. Spec. Top., 2022, 231(16), 3029–3041. [29] X. Wang, N. V. Kuznetsov and G. Chen, Chaotic Systems with Multistability and Hidden Attractors, 40, Springer, 2021. [30] Z. Wei, Dynamical behaviors of a chaotic system with no equilibria, Phys. Lett. A, 2011, 376(2), 102–108. doi: 10.1016/j.physleta.2011.10.040 [31] Z. Wei, I. Moroz, J. Sprott, et al., Hidden hyperchaos and electronic circuit application in a 5D self-exciting homopolar disc dynamo, Chaos, 2017, 27(3), 033101. doi: 10.1063/1.4977417 [32] S. Wiggins, Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2, Springer Science & Business Media, 2003. [33] D. Wilczak, S. Serrano and R. Barrio, Coexistence and dynamical connections between hyperchaos and chaos in the 4D Rössler system: a computer-assisted proof, SIAM J. Appl. Dyn. Syst., 2016, 15(1), 356–390. doi: 10.1137/15M1039201 [34] J. Wu, C. Li, X. Ma, et al., Simplification of chaotic circuits with quadratic nonlinearity, IEEE Trans. Circuits Syst. Ⅱ, 2021, 69(3), 1837–1841. [35] J. Yang, Z. Feng and Z. Liu, A new five-dimensional hyperchaotic system with six coexisting attractors, Qual. Theor. Dyn. Syst., 2021, 20(1), 1–31. doi: 10.1007/s12346-020-00443-9 [36] Q. Yang and M. Bai, A new 5D hyperchaotic system based on modified generalized Lorenz system, Nonlinear Dyn., 2017, 88(1), 189–221. doi: 10.1007/s11071-016-3238-7 [37] Q. Yang, L. Yang and B. Ou, Hidden hyperchaotic attractors in a new 5D system based on chaotic system with two stable node-foci, Int. J. Bifurcation Chaos, 2019, 29(07), 1950092. doi: 10.1142/S0218127419500925 [38] T. Yang and Q. Yang, A 3D autonomous system with infinitely many chaotic attractors, Int. J. Bifurcation Chaos, 2019, 29(12), 1950166. doi: 10.1142/S0218127419501669 [39] F. Yu, L. Liu, B. He, et al., Analysis and fpga realization of a novel 5D hyperchaotic four-wing memristive system, active control synchronization, and secure communication application, Complexity, 2019, 2019, 4047957. [40] F. Yu, L. Liu, S. Qian, et al., Chaos-based application of a novel multistable 5D memristive hyperchaotic system with coexisting multiple attractors, Complexity, 2020, 2020, 1–19. [41] X. Zhang and G. Chen, Constructing an autonomous system with infinitely many chaotic attractors, Chaos, 2017, 27(7), 071101. [42] X. Zhang and C. Wang, Multiscroll hyperchaotic system with hidden attractors and its circuit implementation, Int. J. Bifurcation Chaos, 2019, 29(09), 1950117. [43] Z. Zhang and L. Huang, A new 5D Hamiltonian conservative hyperchaotic system with four center type equilibrium points, wide range and coexisting hyperchaotic orbits, Nonlinear Dyn., 2022, 108(1), 637–652. [44] M. Zhao, Q. Yang and X. Zhang, Dynamics of a class of chua's oscillator with a smooth periodic nonlinearity: Occurrence of infinitely many attractors, Commun. Nonlinear. Sci. Numer. Simul., 2022, 115, 106744. -
-
Figures(17) / Tables(3)
Export File
Citation
Jiaopeng Yang, Pengxian Zhu. A NOVEL 5D SYSTEM GENERATED INFINITELY MANY HYPERCHAOTIC ATTRACTORS WITH THREE POSITIVE LYAPUNOV EXPONENTS[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2843-2873. doi: 10.11948/20230016
Format
Content
DownLoad:
-
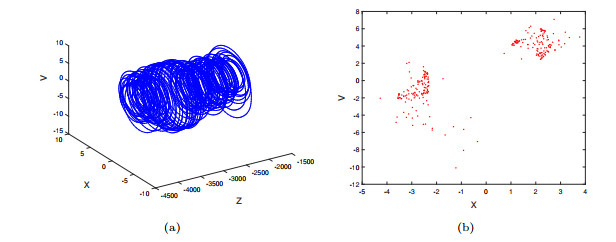
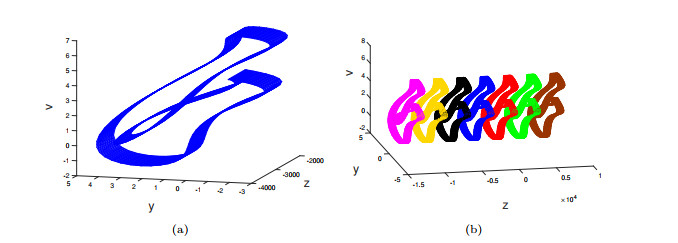
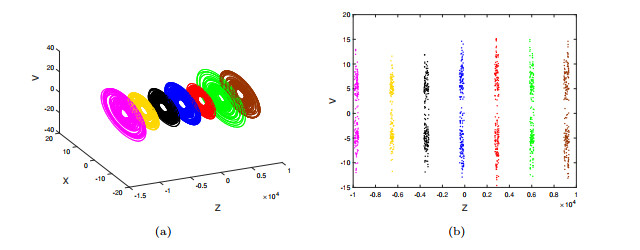
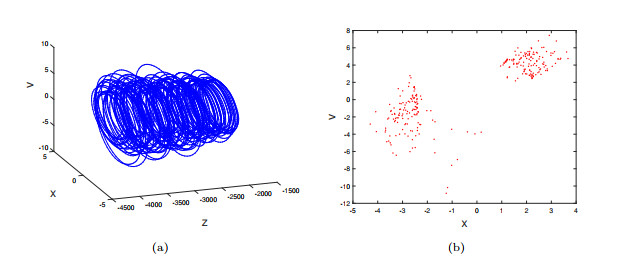
Figure 1.
System (2.1) with parameter set
$ (A_1) $ $ \mathcal{A}_0 $ $ x-v $ $ y=0 $ -
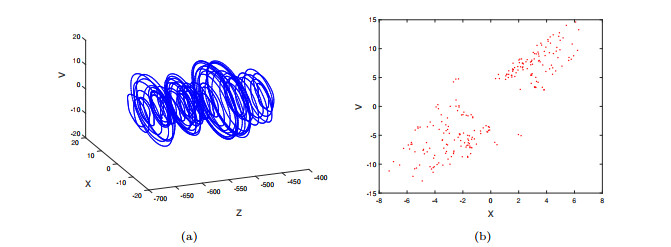
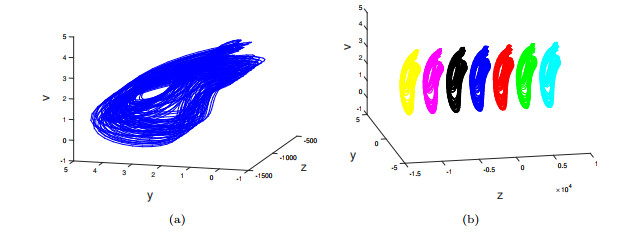
Figure 2.
System (2.1) with parameters set
$ (A_2) $ $ \mathcal{B}_0 $ $ x-v $ $ y=0 $ -
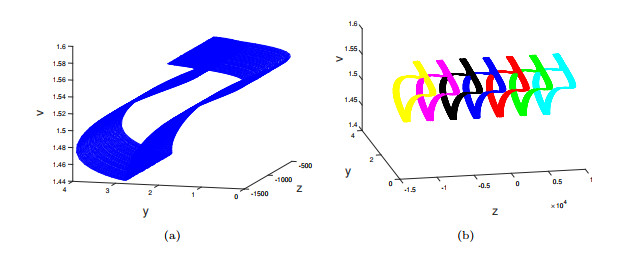
Figure 3.
System (2.1) with parameter set
$ (A_3) $ $ \mathcal{C}_0 $ $ x-v $ $ y=0 $ -
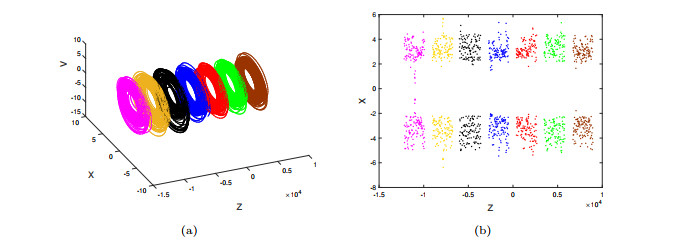
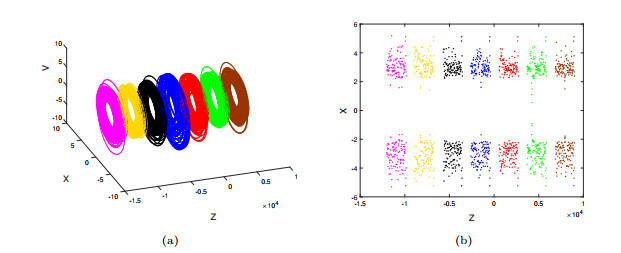
Figure 4.
Coexistence of hidden hyperchaotic attractors
$ \mathcal{A}_m $ $ m=0, \pm1, \pm2, \pm3 $ $ x-z-v $ $ z-x $ $ v=0 $ -
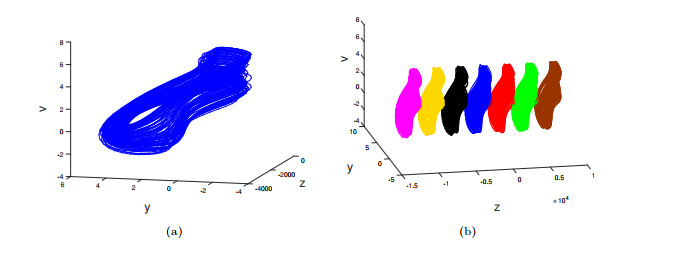
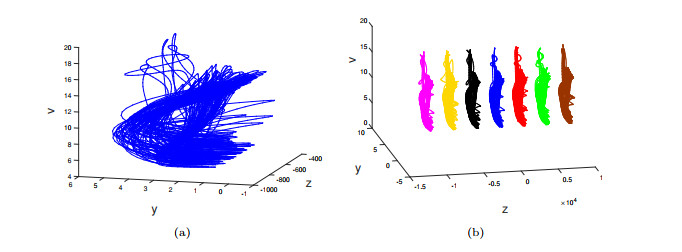
Figure 5.
Projection of attractor on
$ z-y-v $ $ \mathcal{D}_0^{(1)} $ $ \mathcal{D}_m^{(1)} $ -
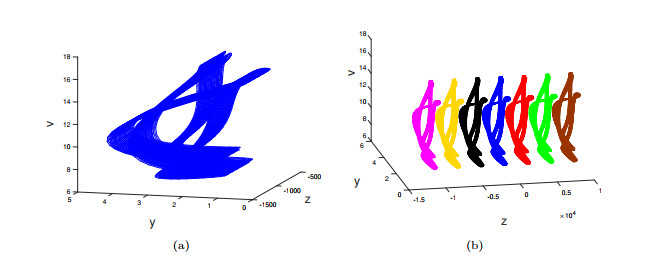
Figure 6.
Projection of attractor on
$ z-y-v $ $ \mathcal{D}_0^{(2)} $ $ \mathcal{D}_m^{(2)} $ -
Figure 7.
System (2.1) with parameter set
$ (A_2) $ $ \mathcal{B}_m $ $ z-x $ $ v=0 $ -
Figure 8.
Projection of attractor on
$ z-y-v $ $ \mathcal{E}_0^{(1)} $ $ \mathcal{E}_m^{(1)} $ -
Figure 9.
Projection of attractor on
$ z-y-v $ $ \mathcal{E}_0^{(2)} $ $ \mathcal{E}_m^{(2)} $ -
Figure 10.
System (2.1) with parameters set
$ (A_3) $ $ \mathcal{C}_m $ $ z-v $ $ y=0 $ -
Figure 11.
Projection of attractor on
$ z-y-v $ $ \mathcal{F}_0^{(1)} $ $ \mathcal{F}_m^{(1)} $ -
Figure 12.
Projection of attractor on
$ z-y-v $ $ \mathcal{F}_0^{(2)} $ $ \mathcal{F}_m^{(2)} $ -
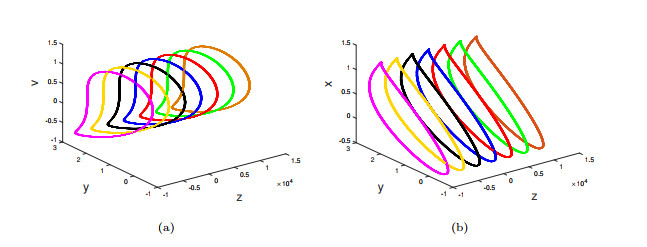
Figure 13.
Projection of periodic attractor: (a) coexistence of periodic attractor
$ \mathcal{G}_m $ $ z-y-v $ $ \mathcal{G}_m $ $ z-y-x $ -
Figure 14.
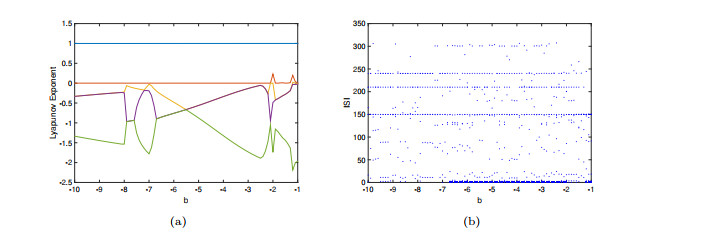
System (2.1) with parameters
$ a=1 $ $ c=5 $ $ d=-3 $ $ e=10 $ $ f=-10 $ $ g=3 $ $ h_1=-2 $ $ h_2=1 $ $ l=-0.2 $ $ k=-4.5 $ $ b\in [-10, -1] $ -
Figure 15.
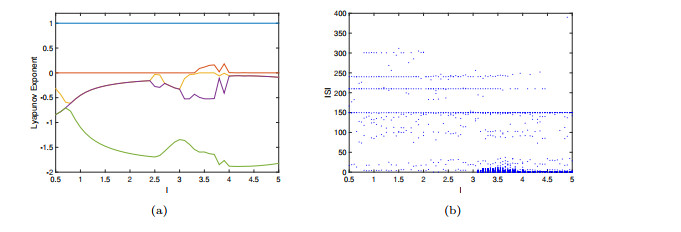
System (2.1) with parameters
$ a=1 $ $ b=-1.12 $ $ d=-3 $ $ e=5 $ $ f=-10 $ $ g=3 $ $ h_1=-2 $ $ h_2=1 $ $ k=-4.5 $ $ l\in [0.5, 5] $ $ c=\frac{1}{gl}(egk-dfk) $ -
Figure 16.
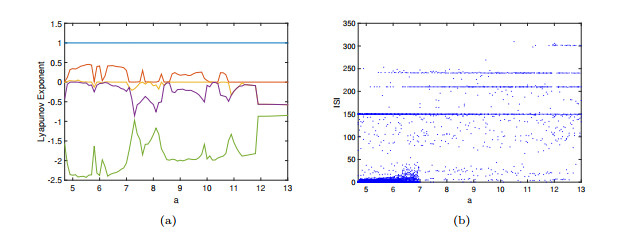
System (2.1) with parameters
$ b=-1.12 $ $ c=5 $ $ d=-3 $ $ e=10 $ $ f=-10 $ $ g=3 $ $ h_1=-2 $ $ h_2=1 $ $ l=8 $ $ k=-4.5 $ $ a\in [4.7, 13] $ -
Figure 17.
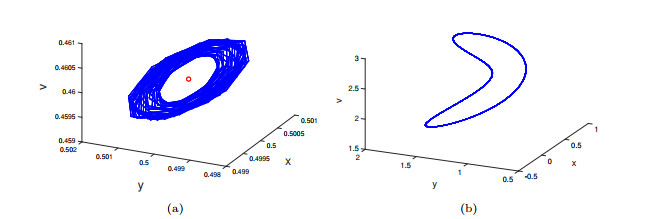
System (2.1) with parameters
$ ( a, c, d, e, f, g, h_1, h_2, l, k) =(1, 5, -2, 2, -1, 2, 1, -1, 1, -2) $ $ b=-1.92 $ $ b=-2 $