| Citation: | Reetika Chawla, Komal Deswal, Devendra Kumar. A NEW NUMERICAL APPROACH OF SOLVING FRACTIONAL MOBILE-IMMOBILE TRANSPORT EQUATION USING ATANGANA-BALEANU DERIVATIVE[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2874-2895. doi: 10.11948/20230044 |
A NEW NUMERICAL APPROACH OF SOLVING FRACTIONAL MOBILE-IMMOBILE TRANSPORT EQUATION USING ATANGANA-BALEANU DERIVATIVE
-
Abstract
A numerical scheme comprising the Crank-Nicolson difference sch-eme in the temporal direction and cubic trigonometric $B$-spline method in the spatial direction is examined for the numerical solution of the variable coefficient time-fractional mobile-immobile solute transport equation. The time-fractional derivative is evaluated using the Atangana-Baleanu Caputo derivative. The equation has advection, dispersion, and reaction coefficients that can be influenced simultaneously by space and time variables. The present numerical scheme is unconditionally stable and second-order convergent in the temporal and spatial directions. Several test problems are solved to confirm the theoretical results.
-

-
References
[1] A. Atangana and D. Baleanu, New fractional derivatives with non-local and non-singular kernel: theory and application to heat transfer model, Therm. Sci., 2016, 20, 763–769. doi: 10.2298/TSCI160111018A [2] E. Bas and R. Ozarslan, Real world applications of fractional models by Atangana-Baleanu fractional derivative, Chaos Solitions Fractals, 2018, 116, 121–125. doi: 10.1016/j.chaos.2018.09.019 [3] C. D. Boor, On the convergence of odd-degree spline interpolation, J. Approx. Theory, 1968, 1(4), 452–463. doi: 10.1016/0021-9045(68)90033-6 [4] M. Caputo and M. Fabrizio, A new definition of fractional derivative without singular kernel, Progr. Fract. Differ. Appl., 2015, 1(2), 73–85. [5] R. Chawla, K. Deswal, D. Kumar and D. Baleanu, A novel finite difference based numerical approach for Modified Atangana-Baleanu Caputo derivative, AIMS Math., 2022, 7(9), 17252–17268. doi: 10.3934/math.2022950 [6] R. Chawla, K. Deswal and D. Kumar, A new numerical formulation for the generalized time-fractional Benjamin Bona Mohany Burgers' equation, Int. J. Nonlinear Sci. Numer. Simul., 2022. DOI: 10.1515/ijnsns-2022-0209. [7] C. Chen, H. Liu, X. Zheng and H. Wang, A two-grid MMOC finite element method for nonlinear variable-order time-fractional mobile/immobile advection-diffusion equations, Comput. Math. Appl., 2020, 79(9), 2771–2783. doi: 10.1016/j.camwa.2019.12.008 [8] G. Gao, H. Zhan, S. Feng, B. Fu, Y. Ma and G. Huang, A new mobile-immobile model for reactive solute transport with scale-dependent dispersion, Water Resour. Res., 2010. DOI: 10.1029/2009WR008707. [9] G. Gao and Z. Sun, A compact finite difference scheme for the fractional sub-diffusion equations, J. Comput. Phys., 2011, 230(3), 586–595. doi: 10.1016/j.jcp.2010.10.007 [10] W. Gao, B. Ghanbari and H. M. Baskonus, New numerical simulations for some real world problems with Atangana-Baleanu fractional derivative, Chaos Solitions Fractals, 2019, 128, 34–43. doi: 10.1016/j.chaos.2019.07.037 [11] H. R. Ghehsareh, A. Zaghian and M. Raei, A local weak form meshless method to simulate a variable order time-fractional mobile-immobile transport model, Eng. Anal. Bound. Elem., 2018, 90, 63–75. doi: 10.1016/j.enganabound.2018.01.016 [12] A. Golbabai, O. Nikan and T. Nikazad, Numerical investigation of the time fractional mobile-immobile advection-dispersion model arising from solute transport in porous media, Int. J. Appl. Comput. Math., 2019, 5, 1–22. doi: 10.1007/s40819-018-0585-8 [13] C. A. Hall, On error bounds for spline interpolation, J. Approx. Theory, 1968, 1(2), 209–218. doi: 10.1016/0021-9045(68)90025-7 [14] M. Hamid, M. Usman, R. U. Haq and W. Wang, A Chelyshkov polynomial based algorithm to analyze the transport dynamics and anomalous diffusion in fractional model, Physica A, 2020, 551, 124227. doi: 10.1016/j.physa.2020.124227 [15] A. A. Hamou, E. H. Azroul, Z. Hammouch and A. L. Alaoui, A monotone iterative technique combined to finite element method for solving reaction-diffusion problems pertaining to non-integer derivative, Eng. Comput., 2022, DOI: 10.1007/s00366-022-01635-4. [16] M. H. Heydari and A. Atangana, An optimization method based on the generalized Lucas polynomials for variable-order space-time fractional mobile-immobile advection-dispersion equation involving derivatives with non-singular kernels, Chaos Solitions Fractals, 2020, 132, 109588. doi: 10.1016/j.chaos.2019.109588 [17] A. S. V. Kanth and S. Deepika, Application and analysis of spline approximation for time fractional mobile-immobile advection-dispersion equation, Numer. Methods Partial Differ. Equ., 2018, 34(5), 1799–1819. doi: 10.1002/num.22266 [18] A. S. V. Kanth and N. Garg, A numerical approach for a class of time-fractional reaction-diffusion equation through exponential B-spline method, Comput. Appl. Math., 2020, 39, 1–24. doi: 10.1007/s40314-019-0964-8 [19] A. Kumar, A. Bhardwaj and B. V. R. Kumar, A meshless local collocation method for time fractional diffusion wave equation, Comput. Math. Appl., 2019, 78(6), 1851–1861. doi: 10.1016/j.camwa.2019.03.027 [20] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier Science, Publishers BV, Amsterdam, 2006. [21] X. Li, Z. Wen, Q. Zhu and H. Jakada, A mobile-immobile model for reactive solute transport in a radial two-zone confined aquifer, J. Hydrol., 2020, 580, 124347. doi: 10.1016/j.jhydrol.2019.124347 [22] F. Liu, P. Zhuang, I. Turner, K. Burrage and V. Anh, A new fractional finite volume method for solving the fractional diffusion equation, Appl. Math. Model., 2014, 38(15–16), 3871–3878. doi: 10.1016/j.apm.2013.10.007 [23] Y. Liu, M. Zhang, H. Li and J. Li, High-order local discontinuous Galerkin method combined with WSGD-approximation for a fractional subdiffusion equation, Comput. Math. Appl., 2017, 73(6), 1298–1314. doi: 10.1016/j.camwa.2016.08.015 [24] Z. Liu and X. Li, A Crank-Nicolson difference scheme for the time variable fractional mobile-immobile advection-dispersion equation, J. Appl. Math. Comput., 2018, 56(1–2), 391–410. doi: 10.1007/s12190-016-1079-7 [25] Z. Liu, X. Li and X. Zhang, A fast high-order compact difference method for the fractal mobile/immobile transport equation, Int. J. Appl. Comput. Math., 2020, 97(9), 1860–1883. [26] B. Maayah, O. A. Arqub, S. Alnabulsi and H. Alsulami, Numerical solutions and geometric attractors of a fractional model of the cancer-immune based on the Atangana-Baleanu-Caputo derivative and the reproducing kernel scheme, Chinese J. Phys., 2022, 80, 463–483. doi: 10.1016/j.cjph.2022.10.002 [27] P. Perdikaris and G. E. Karniadakis, Fractional-order viscoelasticity in one-dimensional blood flow models, Ann. Biomed. Eng., 2014, 42, 1012–1023. doi: 10.1007/s10439-014-0970-3 [28] I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999. [29] S. S. Ray, A novel wavelets operational matrix method for the time variable-order fractional mobile-immobile advection-dispersion model, Eng. Comput., 2021. DOI: 10.1007/s00366-021-01405-8. [30] K. Sadri and H. Aminikhah, An efficient numerical method for solving a class of variable-order fractional mobile-immobile advection-dispersion equations and its convergence analysis, Chaos Solitions Fractals, 2021, 146, 110896. doi: 10.1016/j.chaos.2021.110896 [31] R. Schumer, D. A. Benson, M. M. Meerschaert and B. Baeumer, Fractal mobile/immobile solute transport, Water Resour. Res., 2003, 39(10), 1296. [32] M. Saffarian and A. Mohebbi, An efficient numerical method for the solution of 2D variable order time fractional mobile-immobile advection-dispersion model, Math. Meth. Appl. Sci., 2021, 44(7), 5908–5929. doi: 10.1002/mma.7158 [33] M. Shafiq, M. Abbas, K. M. Abualnaja, A. Majeed and T. Nazir, An efficient technique based on cubic B-spline functions for solving time-fractional advection diffusion equation involving Atangana-Baleanu derivative, Eng. Comput., 2021. DOI: 10.1007/s00366-021-01490-9. [34] F. Song and C. Xu, Spectral direction splitting methods for two-dimensional space fractional diffusion equations, J. Comput. Phys., 2015, 299, 196–214. doi: 10.1016/j.jcp.2015.07.011 [35] X. Yang, H. Zhang and Q. tang, A spline collocation method for a fractional mobile-immobile equation with variable coefficients, Comput. Appl. Math., 2020. DOI:10.1007/s40314-019-1013-3. [36] M. Zhang, Y. Liu and H. Li, High-order local discontinuous Galerkin method for a fractal mobile/immobile transport equation with the Caputo-Fabrizio fractional derivative, Numer. Methods Partial Differ. Equ., 2019, 35(4), 1588–1612. doi: 10.1002/num.22366 [37] Y. Zhao, W. Bu, J. Huang, D. Liu and Y. Tang, Finite element method for two-dimensional space-fractional advection-dispersion equations, Appl. Math. Comput., 2015, 257, 553–565. -
-
-
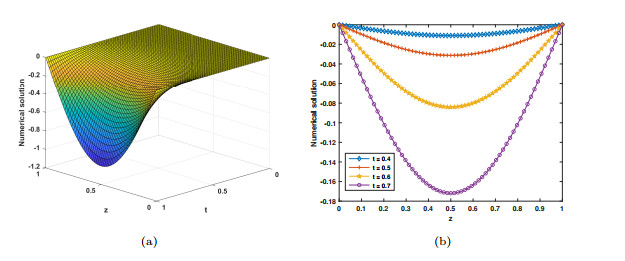
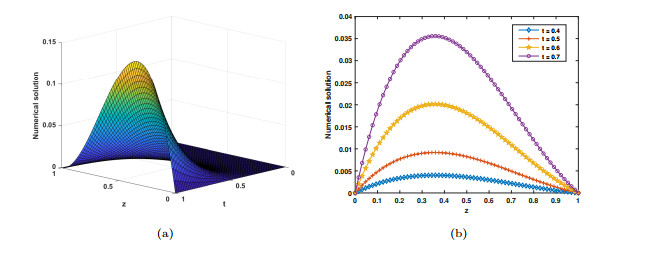
Figure 1.
Plots depicting the behavior of numerical solution at
$ \alpha=0.5 $ -
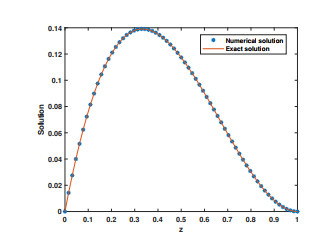
Figure 2.
Line plots of the exact and numerical solutions for Example 6.1 at
$ t=0.5 $ $ \alpha=0.5 $ -
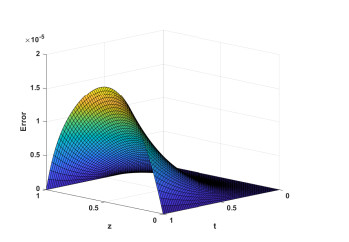
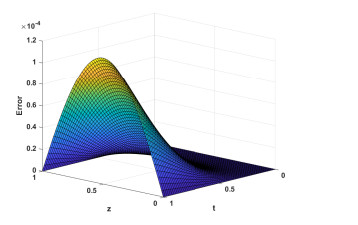
Figure 3.
Error plot for
$ \alpha = 0.5 $ -
Figure 4.
Plots depicting the behavior of numerical solution at
$ \alpha=0.9 $ -
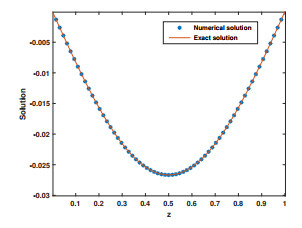
Figure 5.
Line plots of the exact and numerical solution for Example 6.2 for
$ \alpha=0.9 $ $ t = 0.5 $ -
Figure 6.
Error plot for
$ \alpha = 0.9 $




 DownLoad:
DownLoad: