| Citation: |
A. Tripathy, S. Sahoo, S. Saha Ray, M. A. Abdou. COMPLEX NONLINEAR EVOLUTION EQUATIONS IN THE CONTEXT OF OPTICAL FIBERS: NEW WAVE-FORM ANALYSIS[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3442-3460. doi: 10.11948/20230080
|
COMPLEX NONLINEAR EVOLUTION EQUATIONS IN THE CONTEXT OF OPTICAL FIBERS: NEW WAVE-FORM ANALYSIS
-
Abstract
In this study, the new waveforms of two nonlinear evolution models are investigated by an analytical method, namely the sigmoid function method. The considered nonlinear complex models for this are the full nonlinearity form of the Fokas-Lenells equation and the paraxial wave equation, which play an important role in the field of fiber optics by balancing the nonlinearity with the dispersion terms. Under different numeric values of the free terms, the obtained results represent varieties of wave shapes, specifically anti-kink, dark, bright, singular soliton, anti-peakon, kink, two-lump propagation during breather periodic form, single lump, two lump solutions, periodic peakon, and periodic wave solutions, which have not been obtained in the previous studies. These dynamical characteristics are discussed in detail with the help of a pictorial presentation of the derived solutions. These resultants of both the considered nonlinear equations can be useful in both fiber optics as well as in other optics-related fields.
-
-
References
[1] I. Ahmed, A. R. Seadawy and D. Lu, M-shaped rational solitons and their interaction with kink waves in the Fokas-lenells equation, Physica Scripta, 2019, 94(5), 055205. doi: 10.1088/1402-4896/ab0455 [2] M. A. Akbar, A. M. Wazwaz, F. Mahmud, et al., Dynamical behavior of solitons of the perturbed nonlinear Schrödinger equation and microtubules through the generalized Kudryashov scheme, Results in Physics, 2022, 43, 106079. doi: 10.1016/j.rinp.2022.106079 [3] L. Akinyemi and E. Morazara, Integrability, multi-solitons, breathers, lumps and wave interactions for generalized extended Kadomtsev–Petviashvili equation, Nonlinear Dynamics, 2023, 111(5), 4683–4707. doi: 10.1007/s11071-022-08087-x [4] L. Akinyemi, M. Şenol and O. S. Iyiola, Exact solutions of the generalized multidimensional mathematical physics models via sub-equation method, Mathematics and Computers in Simulation, 2021, 182, 211–233. doi: 10.1016/j.matcom.2020.10.017 [5] K. S. Al-Ghafri, E. V. Krishnan and A. Biswas, Chirped optical soliton perturbation of Fokas-Lenells equation with full nonlinearity, Advances in Difference Equations, 2020, 2020(1). [6] K. Ali, S. T. R. Rizvi, B. Nawaz and M. Younis, Optical solitons for paraxial wave equation in Kerr media, Modern Physics Letters B, 2019, 33(3), 1–9. [7] K. K. Ali, M. S. Osman and M. Abdel-Aty, New optical solitary wave solutions of Fokas-Lenells equation in optical fiber via Sine-Gordon expansion method, Alexandria Engineering Journal, 2020, 59(3), 1191–1196. doi: 10.1016/j.aej.2020.01.037 [8] M. Arshad, D. Lu, M. U. Rehman, et al., Optical solitary wave and elliptic function solutions of Fokas-Lenells equation in presence of perturbation terms and its modulation instability, Physica Scripta, 2019, 94(10), 105202. doi: 10.1088/1402-4896/ab1791 [9] M. Arshad, A. R. Seadawy, D. Lu and M. S. Saleem, Elliptic function solutions, modulation instability and optical solitons analysis of the paraxial wave dynamical model with Kerr media, Optical and Quantum Electronics, 2021, 53(1), 1–20. doi: 10.1007/s11082-020-02634-9 [10] S. Arshed, A. Biswas, Q. Zhou, et al., Optical solitons pertutabation with Fokas-Lenells equation by exp(−φ(ξ))-expansion method, Optik, 2019, 179, 341–345. doi: 10.1016/j.ijleo.2018.10.136 [11] S. Arshed and N. Raza, Optical solitons perturbation of Fokas-Lenells equation with full nonlinearity and dual dispersion, Chinese Journal of Physics, 2020, 63, 314–324. doi: 10.1016/j.cjph.2019.12.004 [12] A. Bansal, A. H. Kara, A. Biswas, et al., Optical soliton perturbation, group invariants and conservation laws of perturbed Fokas-Lenells equation, Chaos, Solitons and Fractals, 2018, 114, 275–280. doi: 10.1016/j.chaos.2018.06.030 [13] A. Biswas, Y. Yildirim, E. Yaşar, et al., Optical soliton solutions to Fokas-lenells equation using some different methods, Optik, 2018, 173, 21–31. doi: 10.1016/j.ijleo.2018.07.098 [14] G. Dieu-donne, M. B. Hubert, A. R. Seadawy, et al., Chirped soliton solutions of Fokas–Lenells equation with perturbation terms and the effect of spatio-temporal dispersion in the modulational instability analysis, European Physical Journal Plus, 2020, 135(2). [15] G. Dieu-donne, C. G. L. Tiofack, A. R. Seadawy, et al., Propagation of W-shaped, M-shaped and other exotic optical solitons in the perturbed Fokas-Lenells equation, European Physical Journal Plus, 2020, 135(4). [16] Y. Ding, M. S. Osman and A. M. Wazwaz, Abundant complex wave solutions for the nonautonomous Fokas-Lenells equation in presence of perturbation terms, Optik, 2019, 181, 503–513. doi: 10.1016/j.ijleo.2018.12.064 [17] H. Durur and A. Yokuş, Discussions on diffraction and the dispersion for traveling wave solutions of the (2+1)-dimensional paraxial wave equation, Mathematical Sciences, 2022, 16(3), 269–279. doi: 10.1007/s40096-021-00419-z [18] A. Ebaid, E. R. El-Zahar, A. F. Aljohani, et al., Exact solutions of the generalized nonlinear Fokas-Lennells equation, Results in Physics, 2019, 14, 102472. doi: 10.1016/j.rinp.2019.102472 [19] M. Ekici, Exact solitons in optical metamaterials with quadratic-cubic nonlinearity using two integration approaches, Optik, 2018, 156, 351–355. doi: 10.1016/j.ijleo.2017.11.056 [20] W. Gao, H. F. Ismael, H. Bulut and H. M. Baskonus, Instability modulation for the (2+1)-dimension paraxial wave equation and its new optical soliton solutions in Kerr media, Physica Scripta, 2020, 95(3), 035207. doi: 10.1088/1402-4896/ab4a50 [21] W. Gao, H. F. Ismael, S. A. Mohammed, et al., Complex and real optical soliton properties of the paraxial non-linear Schrödinger equation in kerr media with M-fractional, Frontiers in Physics, 2019, 7, 1–8. doi: 10.3389/fphy.2019.00001 [22] H. F. Ismael, H. Bulut and H. M. Baskonus, Optical soliton solutions to the Fokas-Lenells equation via sine-Gordon expansion method and (m+(G’/G))-expansion method, Pramana-Journal of Physics, 2020, 94(1), 1–9. doi: 10.1007/s12043-019-1882-4 [23] H. F. Ismael, H. Bulut, C. Park and M. S. Osman, M-lump, N-soliton solutions, and the collision phenomena for the (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation, Results in Physics, 2020, 19, 103329. doi: 10.1016/j.rinp.2020.103329 [24] Z. P. Izgi, F. N. Saglam, S. Sahoo, et al., A partial offloading algorithm based on intelligent sensing, International Journal of Modern Physics B, 2022, 36(17), 2250097. doi: 10.1142/S0217979222500977 [25] A. J. M. Jawad, A. Biswas, Q. Zhou, et al., Optical soliton perturbation of Fokas-Lenells equation with two integration schemes, Optik, 2018, 165, 111–116. doi: 10.1016/j.ijleo.2018.03.104 [26] Y. Khan, A novel type of soliton solutions for the Fokas-Lenells equation arising in the application of optical fibers, Modern Physics Letters B, 2020, 2150058, 1–10. [27] M. M. A. Khater, A. M. Alabdali, A. Mashat and S. A. Salama, Optical soliton wave solutions of the fractional complex paraxial wave dynamical model along with kerr media, Fractals, 2022, 30(5), 1–17. [28] N. A. Kudryashov, First integrals and general solution of the Fokas-Lenells equation, Optik, 2019, 195, 163135. doi: 10.1016/j.ijleo.2019.163135 [29] S. Kumar, M. Niwas, M. S. Osman and M. A. Abdou, Abundant different types of exact soliton solution to the (4+1)-dimensional Fokas and (2+1)-dimensional breaking soliton equations, Communications in Theoretical Physics, 2021, 73(10), 105007. doi: 10.1088/1572-9494/ac11ee [30] M. Lakestani and J. Manafian, Novel dark, singular and combo optical solitons for Fokas-Lenells equation, Acta Physica Polonica A, 2019, 136(1), 214–224. doi: 10.12693/APhysPolA.136.214 [31] Z. Li, C. Huang and B. Wang, Phase portrait, bifurcation, chaotic pattern and optical soliton solutions of the Fokas-Lenells equation with cubic-quartic dispersion in optical fibers, Physics Letters A, 2023, 465, 128714. doi: 10.1016/j.physleta.2023.128714 [32] S. Malik, H. Almusawa, S. Kumar, et al., A (2+1)-dimensional Kadomtsev–Petviashvili equation with competing dispersion effect: Painlevé analysis, dynamical behavior and invariant solutions, Results in Physics, 2021, 23, 104043. doi: 10.1016/j.rinp.2021.104043 [33] M. S. Osman and B. Ghanbari, New optical solitary wave solutions of Fokas-Lenells equation in presence of perturbation terms by a novel approach, Optik, 2018, 175, 328–333. doi: 10.1016/j.ijleo.2018.08.007 [34] R. U. Rahman, M. M. M. Qousini, A. Alshehri, et al., Evaluation of the performance of fractional evolution equations based on fractional operators and sensitivity assessment, Results in Physics, 2023, 49, 106537. doi: 10.1016/j.rinp.2023.106537 [35] T. Rasool, R. Hussain, M. A. Al Sharif, et al., A variety of optical soliton solutions for the M-truncated Paraxial wave equation using Sardar-subequation technique, Optical and Quantum Electronics, 2023, 55(5), 396. doi: 10.1007/s11082-023-04655-6 [36] S. S. Ray and S. Sahoo, New exact solutions of time fractional modified kawahara equations in modelling surface tension in shallow-water and capillary gravity water waves, The European Physical Journal Plus, 2017, 132(1), 1–11. doi: 10.1140/epjp/i2017-11280-8 [37] S. Sahoo and S. S. Ray, A new method for exact solutions of variant types of time-fractional Korteweg-de Vries equations in shallow water waves, Math. Methods in the Appl. Sci., 2016, 40(1), 106–114. [38] S. Sahoo and S. Saha Ray, A novel approach for stochastic solutions of wick-type stochastic time-fractional Benjamin–Bona–Mahony equation for modeling long surface gravity waves of small amplitude, Stochastic Analysis and Applications, 2019, 37(3), 377–387. doi: 10.1080/07362994.2019.1569532 [39] M. Savescu, Q. Zhou, L. Moraru, et al., Singular optical solitons in birefringent nano-fibers, Optik, 2016, 127(20), 8995–9000. doi: 10.1016/j.ijleo.2016.06.089 [40] A. Souleymanou, A. Houwe, A. H. Kara, et al., Explicit exact solutions and conservation laws in a medium with competing weakly nonlocal nonlinearity and parabolic law nonlinearity, Optical and Quantum Electronics, 2023, 55(5), 464. doi: 10.1007/s11082-023-04694-z [41] K. U. Tariq, H. Rezazadeh, M. Zubair et al., New Exact and Solitary Wave Solutions of Nonlinear Schamel–KdV Equation, International Journal of Applied and Computational Mathematics, 2022, 8(3), 114. doi: 10.1007/s40819-022-01315-3 [42] K. U. Tariq, H. Zainab, A. R. Seadawy, et al., On some novel optical wave solutions to the paraxial M-fractional nonlinear Schrödinger dynamical equation, Optical and Quantum Electronics, 2021, 53(5), 1–14. [43] A. Tripathy and S. Sahoo, A novel analytical method for solving (2+1)-dimensional extended Calogero-Bogoyavlenskii-Schiff equation in plasma physics, Journal of Ocean Engineering and Science, 2021, 6(4), 405–409. doi: 10.1016/j.joes.2021.04.003 [44] A. Tripathy and S. Sahoo, New optical behaviours of the time–fractional Radhakrishnan–Kundu–Lakshmanan model with Kerr law nonlinearity arise in optical fibers, Optical and Quantum Electronics, 2022, 54(4), 1–16. [45] K. J. Wang and G. D. Wang, Exact traveling wave solutions for the system of the ion sound and Langmuir waves by using three effective methods, Results in Physics, 2022, 35, 105390. doi: 10.1016/j.rinp.2022.105390 -
-
Figures(13)
Export File
Citation
A. Tripathy, S. Sahoo, S. Saha Ray, M. A. Abdou. COMPLEX NONLINEAR EVOLUTION EQUATIONS IN THE CONTEXT OF OPTICAL FIBERS: NEW WAVE-FORM ANALYSIS[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3442-3460. doi: 10.11948/20230080
Format
Content
DownLoad:
-
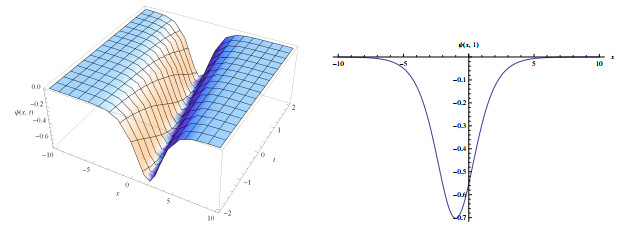
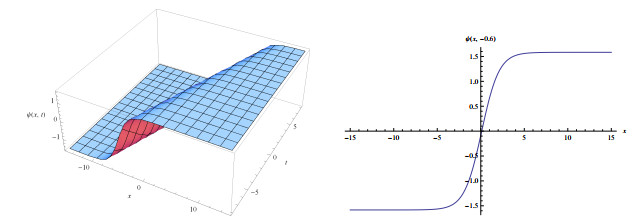
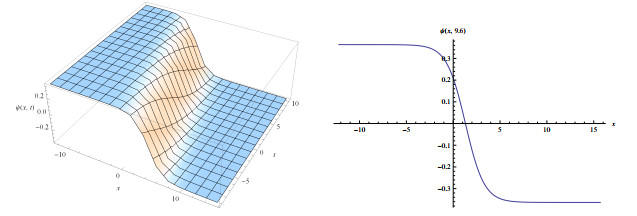
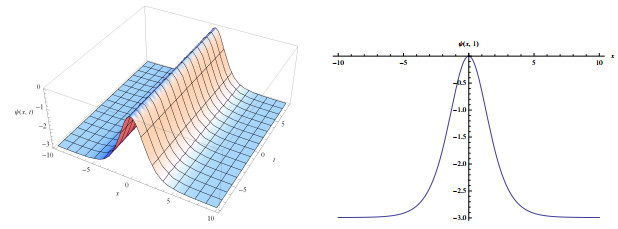
Figure 1.
Wave solutions of eq.(3.5) for
$ a_{1}=-1.2, a_{2}=0.3, \alpha=2, l=0.2, \delta=-1.5 $ $ q=-0.01 $ -
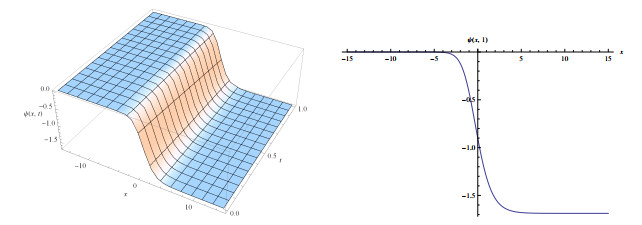
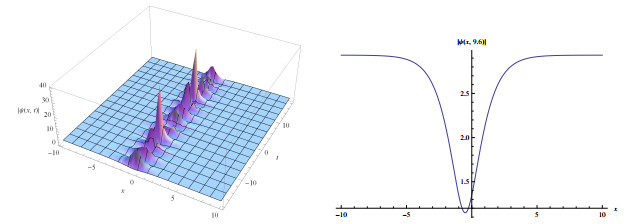
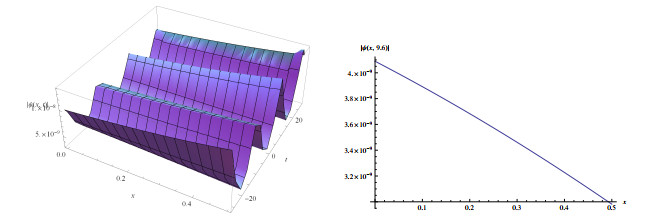
Figure 2.
Wave solutions of eq.(3.7) for
$ a_{1}=1.2, a_{2}=0.3, \alpha=2, l=0.2, \delta=0.5 $ $ q=-1 $ -
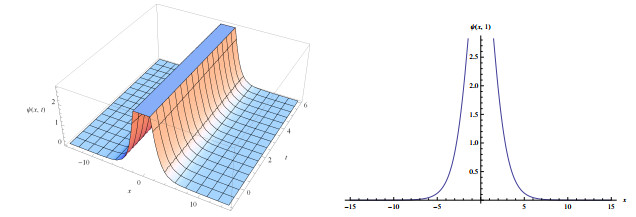
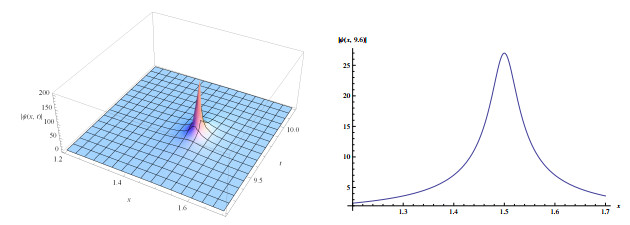
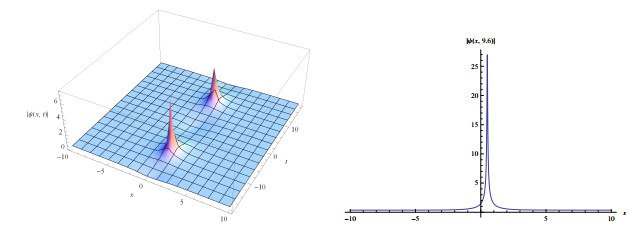
Figure 3.
Wave solutions of eq.(3.9) for
$ a_{1}=-1.2, a_{2}=0.3, \alpha=2, l=0.2, \delta=0.5 $ $ q=-1 $ -
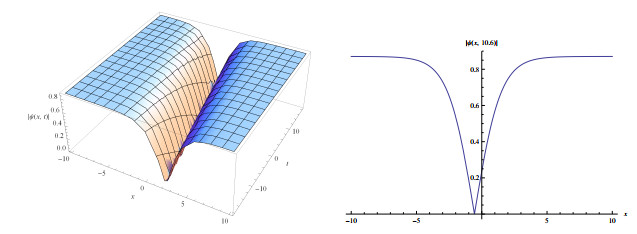
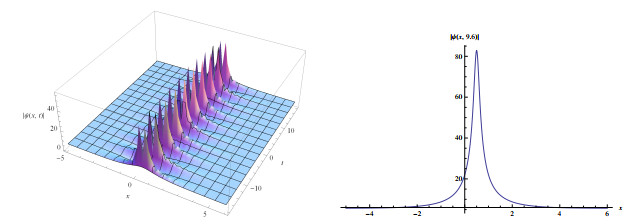
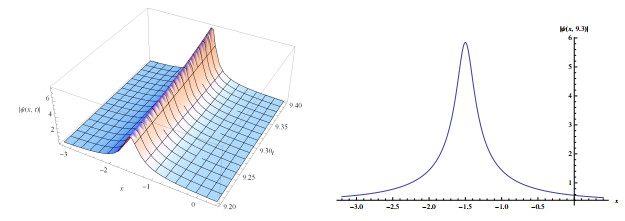
Figure 4.
Wave solutions of eq.(3.10) for
$ a_{1}=-0.2, a_{2}=-0.3, m=2, \alpha=-2, l=-0.2, \delta=0.05 $ $ q=0.01 $ -
Figure 5.
Wave solutions of eq.(3.12) for the values of
$ a_{1}=1.2, m=-0.3, a_{3}=-2, l=-0.2, q=-0.1 $ $ y=-0.5 $ -
Figure 6.
Wave solutions of eq.(3.12) for the values of
$ a_{1}=-1.2, m=-0.3, a_{3}=-1.38, l=0.2, q=0.65 $ $ y=-0.5 $ -
Figure 7.
Wave solutions of eq.(3.13) for the values of
$ a_{1}=-1.2, m=-0.3, a_{3}=1.38, l=0.2 $ $ y=0.5 $ -
Figure 8.
Wave solutions of eq.(3.13) for the values of
$ a_{1}=-1.9, m=-0.3, a_{3}=-1.38, l=-2.2 $ $ y=-1.5 $ -
Figure 9.
Wave solutions of eq.(3.13) for the values of
$ a_{1}=-1.9, m=-0.3, a_{3}=-0.38, l=0.2 $ $ y=-0.5 $ -
Figure 10.
Wave solutions of eq.(3.14) for the values of
$ a_{1}=1.9, m=-0.3, a_{3}=1.38, l=-2.2 $ $ y=-1.5 $ -
Figure 11.
Wave solutions of eq.(3.14) for the values of
$ a_{1}=-1.9, m=-0.3, a_{3}=-0.38, l=-1.82 $ $ y=-1.5 $ -
Figure 12.
Wave solutions of eq.(3.15) for the values of
$ a_{1}=-1.9, m=-0.3, a_{3}=-1.38, l=-2.2 $ $ y=-0.5 $ -
Figure 13.
Wave solutions of eq.(3.15) for the values of
$ a_{1}=-1.9, m=-0.3, a_{3}=1.38, l=-2.2 $ $ y=1.5 $