| Citation: | Xueqiong Yi, Yuqian Zhou, Qian Liu. TRAVELING WAVES OF THE KDV-NKDV EQUATION[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3461-3476. doi: 10.11948/20230100 |
TRAVELING WAVES OF THE KDV-NKDV EQUATION
-
Abstract
In this paper, we use the dynamical system method to investigate the wave solutions of the KdV-nKdV equation. We prove Wazwaz’s proposal that the KdV-nKdV equation has continuous periodic wave solutions and give their exact expressions by elliptic integral theory. We confirm that the KdV-nKdV equation has no classical solitary wave solution although it can be regarded as a fusion of the KdV equation with classical solitary wave and the nKdV equation. In addition, we obtain some novel traveling wave solutions of it including trapezoidal wave, inverted ‘N’ wave, and blow-up wave solutions.
-
Keywords:
- KdV-nKdV equation /
- bifurcation /
- dynamical system /
- trapezoidal wave /
- inverted ‘N’ wave
-

-
References
[1] P. F. Byrd and M. D. Friedman, Handbook of Elliptic Integrals for Engineers and Physicists, Springer, 2013. [2] J. C. Chen and S. D. Zhu, Residual symmetries and soliton-cnoidal wave interaction solutions for the negative-order Korteweg-de Vries equation, Applied Mathematics Letters, 2017, 73, 136–142. doi: 10.1016/j.aml.2017.05.002 [3] W. G. Cheng and T. Z. Xu, N-th Bäcklund transformation and soliton-cnoidal wave interaction solution to the combined KdV-negative-order KdV equation, Applied Mathematics Letters, 2019, 94, 21–29. doi: 10.1016/j.aml.2019.02.010 [4] S. N. Chow and J. K. Hale, Methods of Bifurcation Theory, Springer Science & Business Media, 2012. [5] M. EKiCi and Ü. Metin, The double (G’/G, 1/G)-expansion method and its applications for some nonlinear partial differential equations, Journal of the Institute of Science and Technology, 2021, 11(1), 599–608. [6] B. L. Guo, X. F. Pang, Y. F. Wang and N. Liu, Solitons, Walter de Gruyter GmbH & Co KG, 2018. [7] T. Y. Han, Z. Li and X. Zhang, Bifurcation and new exact traveling wave solutions to time-space coupled fractional nonlinear Schrödinger equation, Physics Letters A, 2021, 395, 127217. doi: 10.1016/j.physleta.2021.127217 [8] H. C. Hu and F. Y. Liu, Nonlocal symmetries and similarity reductions for Korteweg-de Vries-negative-order Korteweg-de Vries equation, Chinese Physics B, 2020, 29(4), 040201. doi: 10.1088/1674-1056/ab6dca [9] T. Kato, On the Korteweg-de Vries equation, Manuscripta mathematica, 1979, 28(1), 89–99. [10] B. Katzengruber, M. Krupa and P. Szmolyan, Bifurcation of traveling waves in extrinsic semiconductors, Physica D: Nonlinear Phenomena, 2000, 144(1–2), 1–19. doi: 10.1016/S0167-2789(00)00030-0 [11] D. J. Korteweg and G. De Vries, XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1895, 39(240), 422–443. doi: 10.1080/14786449508620739 [12] M. D. Kruskal, The birth of the soliton, Nonlinear evolution equations solvable by the spectral transform, 1978, 26, 1–8. [13] S. Kumar and D. Kumar, 1-Multisoliton and other invariant solutions of combined KdV-nKdV equation by using symmetry approach, 2018, arXiv: 1805.10983. [14] U. Kumar Samanta, A. Saha and P. Chatterjee, Bifurcations of nonlinear ion acoustic travelling waves in the frame of a Zakharov-Kuznetsov equation in magnetized plasma with a kappa distributed electron, Physics of Plasmas, 2013. DOI: 10.1063/1.4804347. [15] J. B. Li and G. R. Chen, Bifurcations of traveling wave solutions in a microstructured solid model, International Journal of Bifurcation and Chaos, 2013, 23(01), 1350009. doi: 10.1142/S0218127413500090 [16] J. B. Li and G. R. Chen, Exact traveling wave solutions and their bifurcations for the Kudryashov-Sinelshchikov equation, International Journal of Bifurcation and Chaos, 2012, 22(05), 1250118. doi: 10.1142/S0218127412501180 [17] J. L. Liang, L. K. Tang, Y. H. Xia and Y. Zhang, Bifurcations and exact solutions for a class of MKdV equations with the conformable fractional derivative via dynamical system method, International Journal of Bifurcation and Chaos, 2020, 30(01), 2050004. doi: 10.1142/S0218127420500042 [18] P. J. Olver, Evolution equations possessing infinitely many symmetries, Journal of Mathematical Physics, 1977, 18(6), 1212–1215. doi: 10.1063/1.523393 [19] Z. J. Qiao, A general approach for getting the commutator representations of the hierarchies of nonlinear evolution equations, Physics Letters A, 1994, 195(5–6), 319–328. doi: 10.1016/0375-9601(94)90036-1 [20] Z. J. Qiao, Finite Dimensional Integrable System and Nonlinear Evolution Equations, Higer Eductation Press, Beijing, 2002. [21] Z. J. Qiao, Commutator representations of three isospectral equation hierarchies, Chin. J. Contemp. Math, 1993, 14, 41. [22] Z. J. Qiao, Generation of the hierarchies of solitons and generalized structure of the commutator representation, Acta. Appl. Math. Sinica, 1995, 18, 287–301. [23] Z. J. Qiao, Generalized structure of lax representations for nonlinear evolution equation, Applied Mathematics and Mechanics, 1997, 18(7), 671–677. doi: 10.1007/BF00127015 [24] Z. J. Qiao, Generalized Lax Algebra, γ-Matrix and Algebro-geometric Solution of Integrable Systems, Fudan University, Shanghai, 1997. [25] Z. J. Qiao, C. W. Cao and W. Strampp, Category of nonlinear evolution equations, algebraic structure, and r-matrix, Journal of Mathematical Physics, 2003, 44(2), 701–722. doi: 10.1063/1.1532769 [26] Z. J. Qiao and E. G. Fan, Negative-order Korteweg-de Vries equations, Physical Review E, 2012, 86(1), 016601. doi: 10.1103/PhysRevE.86.016601 [27] M. Rodriguez, J. Li and Z. J. Qiao, Negative Order KdV Equation with No Solitary Traveling Waves, Mathematics, 2021, 10(1), 48. doi: 10.3390/math10010048 [28] L. J. Shi and Z. S. Wen, Bifurcations and dynamics of traveling wave solutions to a Fujimoto-Watanabe equation, Communications in Theoretical Physics, 2018, 69(6), 631. doi: 10.1088/0253-6102/69/6/631 [29] J. M. Verosky, Negative powers of Olver recursion operators, Journal of mathematical physics, 1991, 32(7), 1733–1736. doi: 10.1063/1.529234 [30] A. M. Wazwaz, A new integrable equation that combines the KdV equation with the negative-order KdV equation, Mathematical Methods in the Applied Sciences, 2018, 41(1), 80–87. doi: 10.1002/mma.4595 [31] Z. S. Wen, Bifurcations and exact traveling wave solutions of the celebrated Green-Naghdi equations, International Journal of Bifurcation and Chaos, 2017, 27(07), 1750114. doi: 10.1142/S0218127417501140 [32] G. A. Xu, Y. Zhang and J. B. Li, Exact solitary wave and periodic-peakon solutions of the complex Ginzburg-Landau equation: Dynamical system approach, Mathematics and Computers in Simulation, 2022, 191, 157–167. doi: 10.1016/j.matcom.2021.08.007 [33] L. J. Zhang and C. M. Khalique, Exact solitary wave and periodic wave solutions of the Kaup-Kuperschmidt equation, J. Appl. Anal. Comput, 2015, 5(3), 485–495. [34] Z. F. Zhang, T. R. Ding, W. Z. Huang and Z. X. Dong, Qualitative Theory of Differential Equations, American Mathematical Society, Providence, RI, USA, 1992. [35] Y. Q. Zhou, F. T. Fan and Q. Liu, Bounded and unbounded traveling wave solutions of the (3+1)-dimensional Jimbo-Miwa equation, Results in Physics, 2019, 12, 1149–1157. doi: 10.1016/j.rinp.2018.12.065 [36] Y. Q. Zhou and Q. Liu, Reduction and bifurcation of traveling waves of the KdV-Burgers-Kuramoto equation, Discrete & Continuous Dynamical Systems-B, 2016, 21(6), 2057. [37] W. J. Zhu and Y. H. Xia, Traveling Wave Solutions of a Generalized Burgers-αβ Equation, Qualitative Theory of Dynamical Systems, 2022, 21(1), 1–11. doi: 10.1007/s12346-021-00531-4 -
-
-
Figure 1.
Transition boundaries on (
$ e-c $ -
Figure 2.
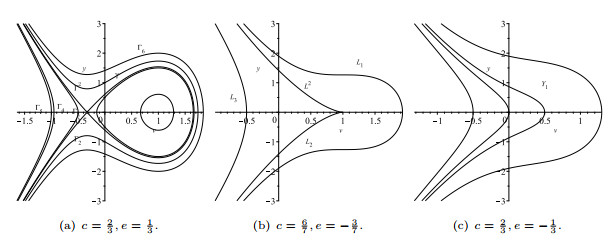
Different phase portraits of system (2.4).
-
Figure 3.
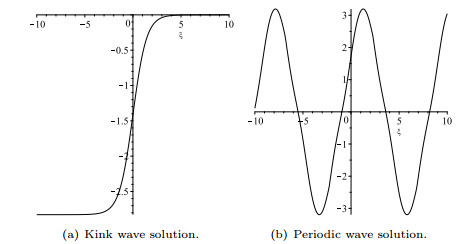
Two kinds of classical wave solutions.
-
Figure 4.
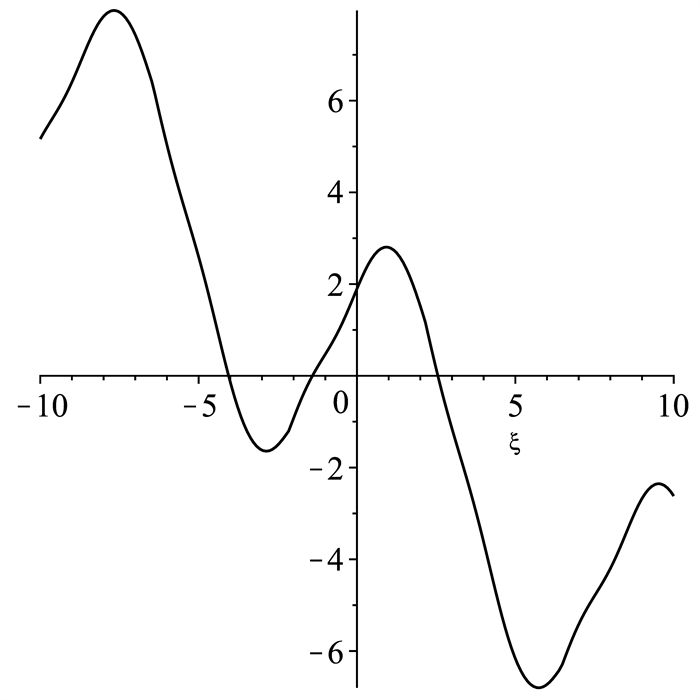
Trapezoidal wave solution.
-
Figure 5.
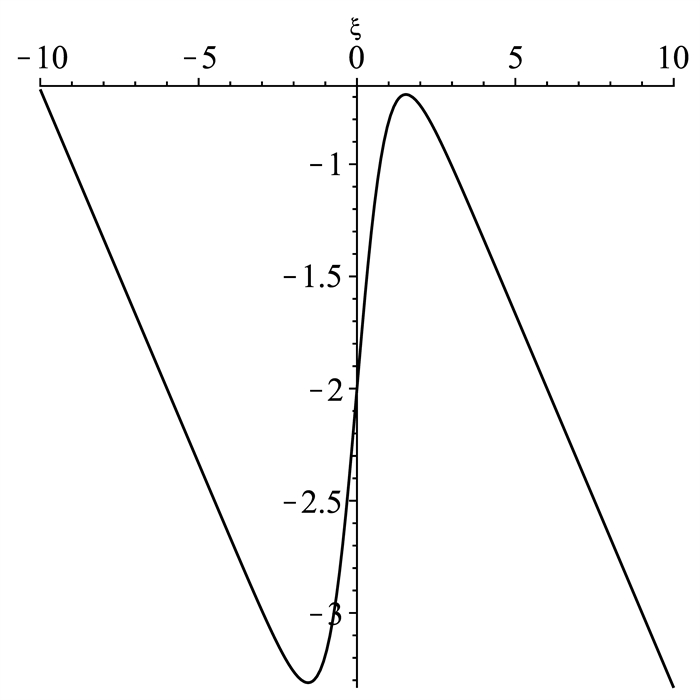
Inverted ‘N’ wave solution.
-
Figure 6.
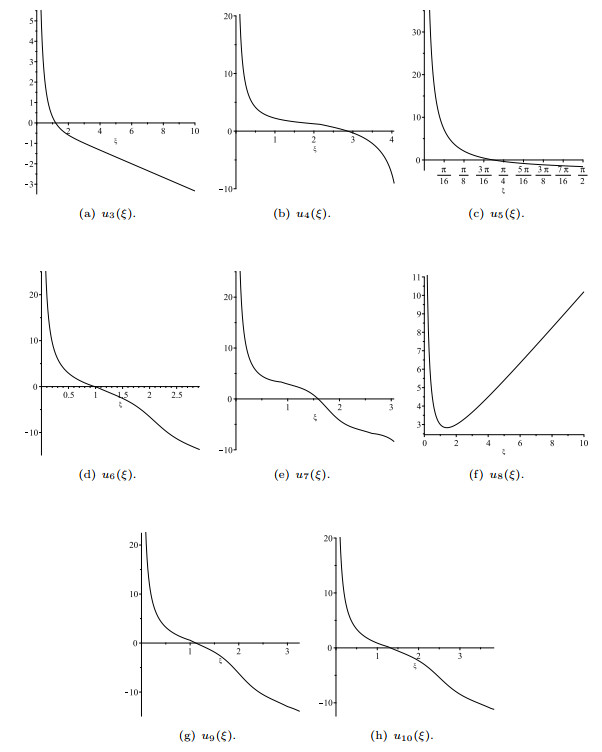
Blow-up wave solutions.





 DownLoad:
DownLoad: