| Citation: | Peixing Yang, Jiang Yu. THE FIRST THREE ORDER MELNIKOV FUNCTIONS FOR GENERAL PIECEWISE HAMILTONIAN SYSTEMS WITH A NON-REGULAR SEPARATION LINE[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1374-1394. doi: 10.11948/20230158 |
THE FIRST THREE ORDER MELNIKOV FUNCTIONS FOR GENERAL PIECEWISE HAMILTONIAN SYSTEMS WITH A NON-REGULAR SEPARATION LINE
-
Abstract
This paper focuses on the first three order Melnikov functions of general planar piecewise Hamiltonian systems under the piecewise perturbations with a non-regular separation line. By using the first three order Melnikov functions, we obtain the exact upper bounds of the number of limit cycles bifurcated from two different piecewise linear near-Hamiltonian systems.
-
Keywords:
- Melnikov functions /
- separation line /
- limit cycles
-

-
References
[1] K. D. S. Andrade, O. A. R. Cespedes, D. R. Cruz and D. D. Novaes, Higher order Melnikov analysis for planar piecewise linear vector fields with nonlinear switching curve, J. Differential Equations, 2021, 287, 1–36. doi: 10.1016/j.jde.2021.03.039 [2] D. C. Braga and L. F. Mello, Limit cycles in a family of discontinuous piecewise linear differential systems with two zones in the plane, Nonlinear Dynam., 2013, 73(3), 1283–1288. doi: 10.1007/s11071-013-0862-3 [3] C. Buzzi, C. Pessoa and J. Torregrosa, Piecewise linear perturbations of a linear center, Discrete Contin. Dyn. Syst., 2013, 33(9), 3915–3936. doi: 10.3934/dcds.2013.33.3915 [4] P. T. Cardin and J. Torregrosa, Limit cycles in planar piecewise linear differential systems with nonregular separation line, Phys. D., 2016, 337, 67–82. doi: 10.1016/j.physd.2016.07.008 [5] J. Chen and M. Han, Bifurcation of limit cycles by perturbing piecewise linear Hamiltonian systems with piecewise polynomials, Internat. J. Bifur Appl. Sci. Engrg., 2023, 33(5), 2350059, p. 27. doi: 10.1142/S0218127423500591 [6] X. Chen, T. Li and J. Llibre, Melnikov functions of arbitrary order for piecewise smooth differential systems in $\mathbb{R}^n$ and applications, J. Differential Equations, 2022, 314, 340–369. doi: 10.1016/j.jde.2022.01.019 CrossRef $\mathbb{R}^n$ and applications" target="_blank">Google Scholar
[7] J. -P. Françoise, Successive derivatives of a first return map, application to the study of quadratic vector fields, Ergodic Theory Dynam. Systems, 1996, 16(1), 87–96. doi: 10.1017/S0143385700008725 [8] M. Han, On the maximum number of periodic solutions of piecewise smooth periodic equations by average method, J. Appl. Anal. Comput., 2017, 7(2), 788–794. [9] M. Han and L. Sheng, Bifurcation of limit cycles in piecewise smooth systems via Melnikov function, J. Appl. Anal. Comput., 2015, 5(4), 809–815. [10] M. Han and J. Yang, The maximum number of zeros of functions with parameters and application to differential equations, J. Nonlinear Model. Anal., 2021, 3, 13–34. [11] W. Hou and S. Liu, Melnikov functions for a class of piecewise Hamiltonian system, J. Nonlinear Model. Anal., 2023, 5, 123–145. [12] T. Li and J. Llibre, Limit cycles of piecewise polynomial differential systems with the discontinuity line $xy=0$, Commun. Pure Appl. Anal., 2021, 20, 3887–3909. [13] T. Li and J. Llibre, Limit cycles in piecewise polynomial Hamiltonian systems allowing nonlinear switching boundaries, J. Differential Equations, 2023, 344, 405–438. doi: 10.1016/j.jde.2022.11.007 [14] S. Liu, M. Han and J. Li, Bifurcation methods of periodic orbits for piecewise smooth systems, J. Differential Equations, 2021, 275, 204–233. doi: 10.1016/j.jde.2020.11.040 [15] X. Liu and M. Han, Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2010, 20(5), 1379–1390. doi: 10.1142/S021812741002654X [16] D. D. Novaes, Higher order stroboscopic averaged functions: a general relationship with Melnikov functions, Electron. J. Qual. Theory Differ. Equ., 2021, 77, 1–9. [17] Y. Xiong and M. Han, Limit cycle bifurcations in discontinuous planar systems with multiple lines, J. Appl. Anal. Comput., 2020, 10(1), 361–377. [18] P. Yang, J. -P. Françoise and J. Yu, Second order Melnikov functions of piecewise Hamiltonian systems, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2020, 30, 2050016, p. 11. doi: 10.1142/S0218127420500169 [19] P. Yang, Y. Yang and J. Yu, Up to second order Melnikov functions for general piecewise Hamiltonian systems with nonregular separation line, J. Differential Equations, 2021, 285, 583–606. doi: 10.1016/j.jde.2021.03.020 -
-
-
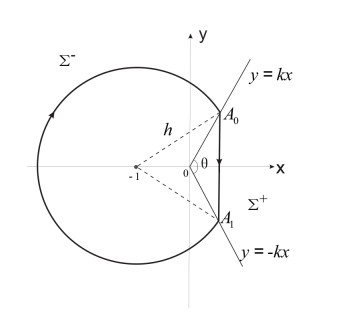
Figure 1.
The perturbed system (1.1).
-
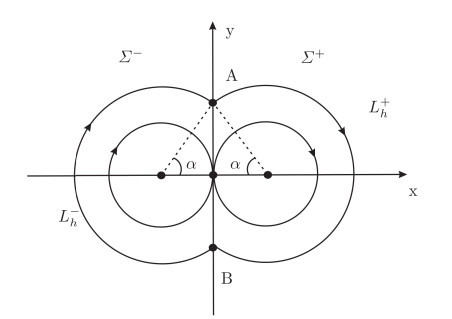
Figure 2.
Unperturbed system (4.2).
-
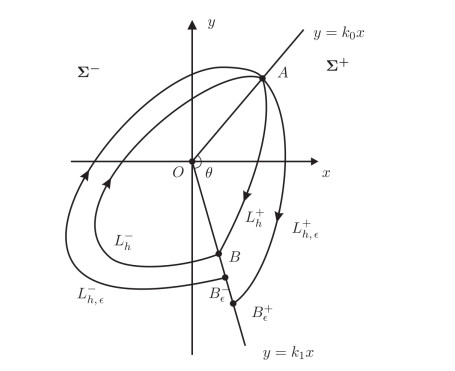
Figure 3.
Unperturbed system (4.11).




 DownLoad:
DownLoad: