| Citation: |
Jiajin He, Min Xiao, Yunxiang Lu, Yonghui Sun, Jinde Cao. QUALITATIVE ANALYSIS OF HIGH-DIMENSIONAL NEURAL NETWORKS WITH THREE-LAYER STRUCTURE AND MUTIPLE DELAYS[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 792-815. doi: 10.11948/20230175
|
QUALITATIVE ANALYSIS OF HIGH-DIMENSIONAL NEURAL NETWORKS WITH THREE-LAYER STRUCTURE AND MUTIPLE DELAYS
-
Abstract
Substantial research has been undertaken on the bifurcation of low-dimensional simplified neural networks. However, how high-dimensional artificial neural networks drive the response dynamics has yet to be fully answered. Back propagation (BP) neural networks, as the basis of many advanced artificial neural networks, possess superior research value. The theoretical analysis of BP neural networks is more sophisticated due to the properties of high dimension and unique structure, and many blind spots still need to be improved urgently. This paper investigates the stability and Hopf bifurcation of an $(n+ 2)$-neuron BP-structured delayed neural network with three layers and $n$ neurons in the hidden layer. Firstly, the Coates flow graph formula is innovatively applied to obtain the characteristic equation. Then, sufficient conditions are deduced to ensure the network's stability and the Hopf bifurcation's occurrence. Finally, numerical simulations are established to demonstrate the theoretical results. It is effectively indicated that the increasing delay will lead to the Hopf bifurcation, ulteriorly bringing about oscillation and instability. Furthermore, the impacts of the self-feedback coefficient and neuron number on the onset of Hopf bifurcation are also revealed.
-
Keywords:
- High-dimensional /
- BP-structured neural network /
- three layers /
- Coates flow graph /
- stability /
- Hopf bifurcation
-
-
References
[1] A. Apicella, F. Donnarumma, F. Isgrò and R. Prevete, A survey on modern trainable activation functions, Neural Netw., 2021, 138, 14-32. doi: 10.1016/j.neunet.2021.01.026 [2] R. V. Aravind and P. Balasubramaniam, Stability criteria for memristor-based delayed fractional-order Cohen-Grossberg neural networks with uncertainties, J. Comput. Appl. Math., 2023, 420, 114764. doi: 10.1016/j.cam.2022.114764 [3] V. N. Balaji, P. B. Srinivas and M. K. Singh, Neuromorphic advancements architecture design and its implementations technique, Mater. Today: Proc., 2022, 51, 850-853. doi: 10.1016/j.matpr.2021.06.273 [4] J. Chen, M. Xiao, Y. Wan, C. Huang and F. Xu, Dynamical bifurcation for a class of large-scale fractional delayed neural networks with complex ring-hub structure and hybrid coupling, IEEE Trans. Neural Netw. Learn. Syst., 2023, 34(5), 2659-2669. doi: 10.1109/TNNLS.2021.3107330 [5] Z. Cheng, D. Li and J. Cao, Stability and Hopf bifurcation of a three-layer neural network model with delays, Neurocomputing, 2016, 175, 355-370. doi: 10.1016/j.neucom.2015.10.068 [6] C. A. Desoer, The optimum formula for the gain of a flow graph or a simple derivation of Coates' formula, Proc. IRE, 1960, 48(5), 883-889. doi: 10.1109/JRPROC.1960.287625 [7] Y. Du, R. Xu and Q. Liu, Stability and bifurcation analysis for a neural network model with discrete and distributed delays, Math. Methods Appl. Sci., 2013, 36(1), 49-59. doi: 10.1002/mma.2568 [8] J. L. Elman, Finding structure in time, Cogn. Sci., 1990, 14(2), 179-211. doi: 10.1207/s15516709cog1402_1 [9] Ö. F. Ertuğrul, A novel type of activation function in artificial neural networks: Trained activation function, Neural Netw., 2018, 99, 148-157. doi: 10.1016/j.neunet.2018.01.007 [10] Y. Fei, R. Li, X. Meng and Z. Li, Bifurcations of a fractional-order four-neuron recurrent neural network with multiple delays, Comput. Intell. Neurosci., 2022, 2022, 1779582. [11] J. J. Hopfield, Neural networks and physical systems with emergent collective computational abilities, Proc. Natl. Acad. Sci. USA, 1982, 79(8), 2554-2558. doi: 10.1073/pnas.79.8.2554 [12] C. Huang, J. Cao, A. Alofi, A. AI-Mazrooei and A. Elaiw, Dynamics and control in an $(n+ 2)$-neuron bam network with multiple delays, Nonlinear Dyn., 2017, 87, 313-336. doi: 10.1007/s11071-016-3045-1 CrossRef $(n+ 2)$-neuron bam network with multiple delays" target="_blank">Google Scholar
[13] Y. Huang, Advances in artificial neural networks-methodological development and application, Algorithms, 2009, 2(3), 973-1007. doi: 10.3390/algor2030973 [14] Z. Huang, Q. Yang and J. Cao, Stochastic stability and bifurcation analysis on Hopfield neural networks with noise, Expert Syst. Appl., 2011, 38(8), 10437-10445. doi: 10.1016/j.eswa.2011.02.111 [15] Q. Jiang, L. Zhu, C. Shu and V. Sekar, An efficient multilayer RBF neural network and its application to regression problems, Neural. Comput. Appl., 2022, 34, 4133-4150. doi: 10.1007/s00521-021-06373-0 [16] B. Kosko, Bidirectional associative memories, IEEE Trans. Syst., Man, Cybern., 1988, 18(1), 49-60. doi: 10.1109/21.87054 [17] M. Kuczyński, M. Borchardt, R. Kleiber, A. Könies and C. Nührenberg, Magnetohydrodynamic eigenfunction classification with a neural network, J. Comput. Appl. Math., 2022, 406, 113889. doi: 10.1016/j.cam.2021.113889 [18] J. Li, X. Yao, X. Wang, Q. Yu and Y. Zhang, Multiscale local features learning based on BP neural network for rolling bearing intelligent fault diagnosis, Measurement, 2020, 153, 107419. doi: 10.1016/j.measurement.2019.107419 [19] P. Li, J. Yan, C. Xu and Y. Shang, Dynamic analysis and bifurcation study on fractional-order tri-neuron neural networks incorporating delays, Fractal Fract., 2022, 6(3), 161. doi: 10.3390/fractalfract6030161 [20] S. Li, C. Huang and S. Yuan, Hopf bifurcation of a fractional-order double-ring structured neural network model with multiple communication delays, Nonlinear Dyn., 2022, 108(1), 379-396. doi: 10.1007/s11071-021-07177-6 [21] Y. Li, R. Kalbasi, A. Karimipour M. Sharifpur and J. Meyer, Using of artificial neural networks (ANNs) to predict the rheological behavior of magnesium oxide-water nanofluid in a different volume fraction of nanoparticles, temperatures, and shear rates, Math. Methods Appl. Sci., 2020. DOI: 10.1002/mma.6418. [22] J. Lin, R. Xu and X. Tian, Pattern formation in reaction-diffusion neural networks with leakage delay, J. Appl. Anal. Comput., 2019, 9(6), 2224-2244. [23] Y. Liu, B. Shen and H. Shu, Finite-time resilient H$\infty$ state estimation for discrete-time delayed neural networks under dynamic event-triggered mechanism, Neural Netw., 2020, 121, 356-365. doi: 10.1016/j.neunet.2019.09.006 CrossRef $\infty$ state estimation for discrete-time delayed neural networks under dynamic event-triggered mechanism" target="_blank">Google Scholar
[24] Y. Lu, M. Xiao, J. He and Z. Wang, Stability and bifurcation exploration of delayed neural networks with radial-ring configuration and bidirectional coupling, IEEE Trans. Neural Netw. Learn. Syst., 2023. DOI: 10.1109/TNNLS.2023.3240403. [25] W. S. McCulloch and W. Pitts, A logical calculus of the ideas immanent in nervous activity, Bull. Math. Biol., 1943, 5, 115-133. [26] F. K. Oduro-Gyimah and K. O. Boateng, Evaluation of single-input single-output radial basis function neural network in modelling empirical 4G traffic, in 2019 International Conference on Mechatronics, Remote Sensing, Information Systems and Industrial Information Technologies, IEEE, 2020, 1, 1-5. [27] X. Ruan, Y. Zhu, J. Li and Y. Cheng, Predicting the citation counts of individual papers via a BP neural network, J. Informetr., 2020, 14(3), 101039. doi: 10.1016/j.joi.2020.101039 [28] D. E. Rumelhart, G. E. Hinton and R. J. Williams, Learning representations by back-propagating errors, Nature, 1986, 323(6088), 533-536. doi: 10.1038/323533a0 [29] A. Singh and V. S. Sharma, Bifurcations and chaos control in a discrete-time prey-predator model with Holling type-Ⅱ functional response and prey refuge, J. Comput. Appl. Math., 2023, 418, 114666. doi: 10.1016/j.cam.2022.114666 [30] N. Sinha, M. Gupta and D. Rao, Dynamic neural networks: An overview, in Proceedings of IEEE International Conference on Industrial Technology 2000, IEEE, 2000, 1, 491-496. [31] Y. Song, M. Han and J. Wei, Stability and Hopf bifurcation analysis on a simplified BAM neural network with delays, Physica D, 2005, 200(3-4), 185-204. doi: 10.1016/j.physd.2004.10.010 [32] A. Suresh, R. R. Nair, E. Neeba and S. Kumar, Recurrent neural network for genome sequencing for personalized cancer treatment in precision healthcare, Neural Process. Lett., 2021. [33] S. Tamura and M. Tateishi, Capabilities of a four-layered feedforward neural network: Four layers versus three, IEEE Trans. Neural Netw., 1997, 8(2), 251-255. doi: 10.1109/72.557662 [34] B. Tao, M. Xiao, W. X. Zheng, J. Cao and J. Tang, Dynamics analysis and design for a bidirectional super-ring-shaped neural network with $n$ neurons and multiple delays, IEEE Trans. Neural Netw. Learn. Syst., 2020, 32(7), 2978-2992. $n$ neurons and multiple delays" target="_blank">Google Scholar
[35] A. Vaishwar and B. K. Yadav, Stability and Hopf-bifurcation analysis of four dimensional minimal neural network model with multiple time delays, Chinese J. Phys., 2022, 77, 300-318. doi: 10.1016/j.cjph.2022.02.011 [36] A. Waibel, T. Hanazawa, G. Hinton, K. Shikano and K. J. Lang, Phoneme recognition using time-delay neural networks, Psychology Press, London, 2013, 35-61. [37] L. Wang, Q. Song, Z. Zhao, Y. Liu and F. E. Alsaadi, Synchronization of two nonidentical complex-valued neural networks with leakage delay and time-varying delays, Neurocomputing, 2019, 356, 52-59. [38] Q. Wang, Z. Duan, M. Perc and G. Chen, Synchronization transitions on small-world neuronal networks: Effects of information transmission delay and rewiring probability, Europhys. Lett., 2008, 83(5), 50008. doi: 10.1209/0295-5075/83/50008 [39] Y. Wang, J. Cao and C. Huang, Exploration of bifurcation for a fractional-order BAM neural network with $n+ 2$ neurons and mixed time delays, Chaos Solit. Fractals, 2022, 159, 112117. doi: 10.1016/j.chaos.2022.112117 CrossRef $n+ 2$ neurons and mixed time delays" target="_blank">Google Scholar
[40] B. Widrow, A. Greenblatt, Y. Kim and D. Park, The no-prop algorithm: A new learning algorithm for multilayer neural networks, Neural Netw., 2013, 37, 182-188. doi: 10.1016/j.neunet.2012.09.020 [41] R. Xing, M. Xiao, Y. Zhang and J. Qiu, Stability and Hopf bifurcation analysis of an $(n+ m)$-neuron double-ring neural network model with multiple time delays, J. Syst. Sci. Complex., 2022, 35, 159-178. [42] C. Xu and C. Aouiti, Comparative analysis on Hopf bifurcation of integer-order and fractional-order two-neuron neural networks with delay, Int. J. Circuit Theory Appl., 2020, 48(9), 1459-1475. doi: 10.1002/cta.2847 [43] C. Xu, W. Zhang, C. Aouiti, Z. Liu, M. Liao and P. Li, Further investigation on bifurcation and their control of fractional-order bidirectional associative memory neural networks involving four neurons and multiple delays, Math. Methods Appl. Sci., 2023, 46(3), 3091-3114. [44] C. Xu, W. Zhang, Z. Liu and L. Yao, Delay-induced periodic oscillation for fractional-order neural networks with mixed delays, Neurocomputing, 2022, 488, 681-693. [45] S. Yanchuk, P. Perlikowski, O. V. Popovych and P. A. Tass, Variability of spatio-temporal patterns in non-homogeneous rings of spiking neurons, Chaos, 2011, 21(4), 047511. [46] J. Zhang and C. Huang, Dynamics analysis on a class of delayed neural networks involving inertial terms, Adv. Differ. Equ., 2020, 2020(1), 1-12. [47] Y. Zhang, M. Xiao, J. Cao and W. X. Zheng, Dynamical bifurcation of large-scale-delayed fractional-order neural networks with hub structure and multiple rings, IEEE Trans. Syst., Man, Cybern., 2020, 52(3), 1731-1743. [48] L. Zhao, J. Cao and M. Xiao, Hopf bifurcation in fractional-order recurrent neural networks, in 2016 Chinese Control and Decision Conference, IEEE, 2016, 5921-5926. [49] H. Zhou, Z. Qixuan, Z. Jin, T. Luo, Y. Zhang and Z. Xu, Empirical phase diagram for three-layer neural networks with infinite width, Adv. Neural Inf. Process. Syst., 2022, 35, 26021-26033. [50] J. Zhu, Z. Chen and X. Liu, Effects of distance-dependent delay on small-world neuronal networks, Phys. Rev. E, 2016, 93(4), 042417. -
-
Figures(13) / Tables(2)
Export File
Citation
Jiajin He, Min Xiao, Yunxiang Lu, Yonghui Sun, Jinde Cao. QUALITATIVE ANALYSIS OF HIGH-DIMENSIONAL NEURAL NETWORKS WITH THREE-LAYER STRUCTURE AND MUTIPLE DELAYS[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 792-815. doi: 10.11948/20230175
Format
Content
DownLoad:
-
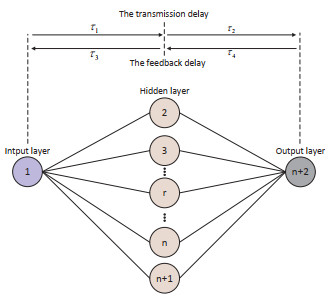
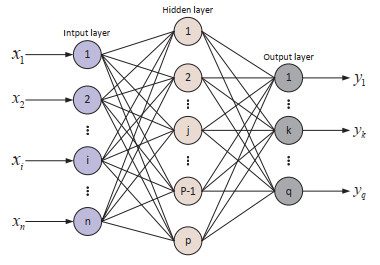
Figure 1.
The general structure of BP neural network.
-
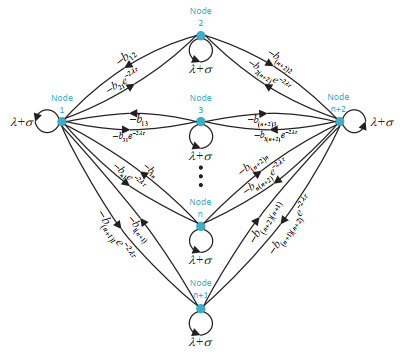
Figure 2.
The structure of an
$ (n+2) $ -
Figure 3.
The flow graph
$ F $ $ \Delta(\lambda) $ -
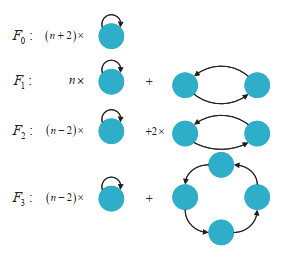
Figure 4.
The four sets
$ F_\eta\; (\eta = 1, 2, 3, 4) $ -
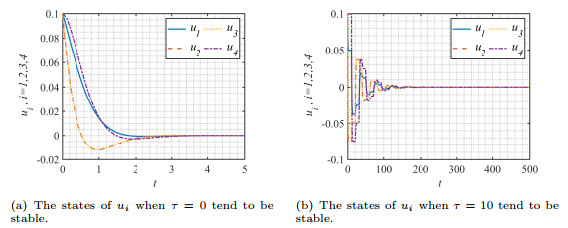
Figure 5.
The waveforms of network (4.1) with
$ \theta=2 $ $ E^* $ $ \tau \geq 0 $ -
Figure 6.
The temporal evolutions of network (4.1) with
$ \theta = 1 $ $ \tau = 0.7 < \tau_0 = 0.785 $ $ E^* $ -
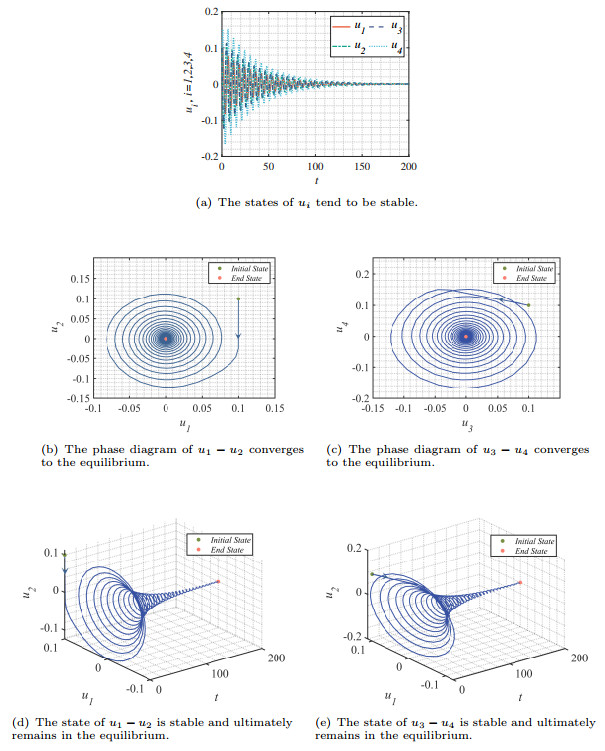
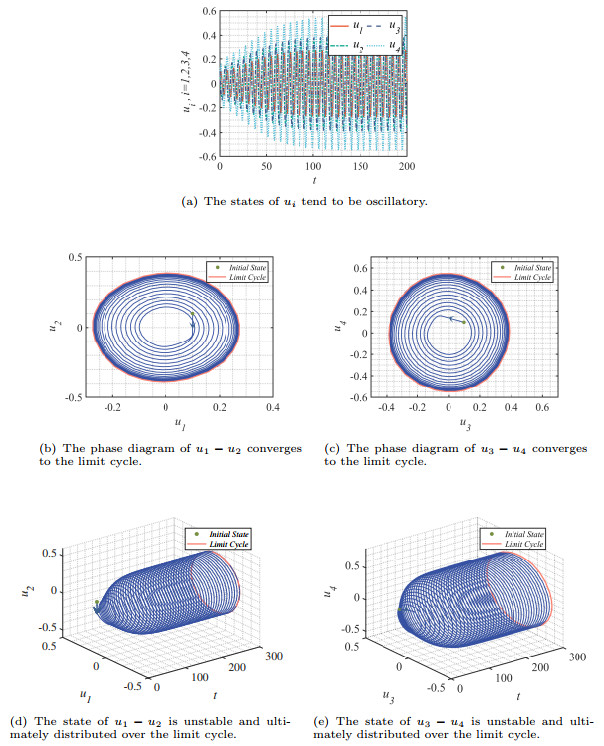
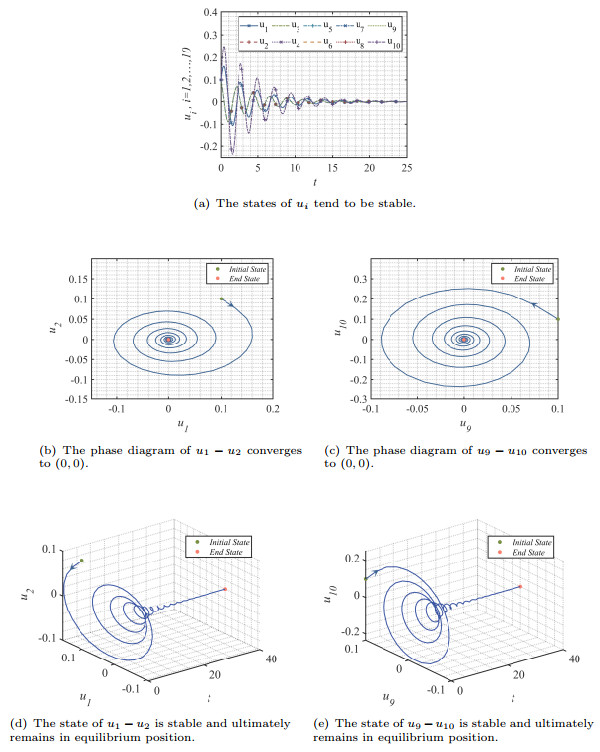
Figure 7.
The temporal evolutions of network (4.1) with
$ \theta = 1 $ $ E^* $ $ \tau = 0.9 > \tau_0 = 0.785 $ -
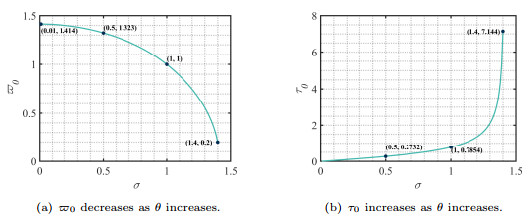
Figure 8.
The fluctuations of critical values
$ \varpi_0 $ $ \tau_0 $ $ \sigma $ -
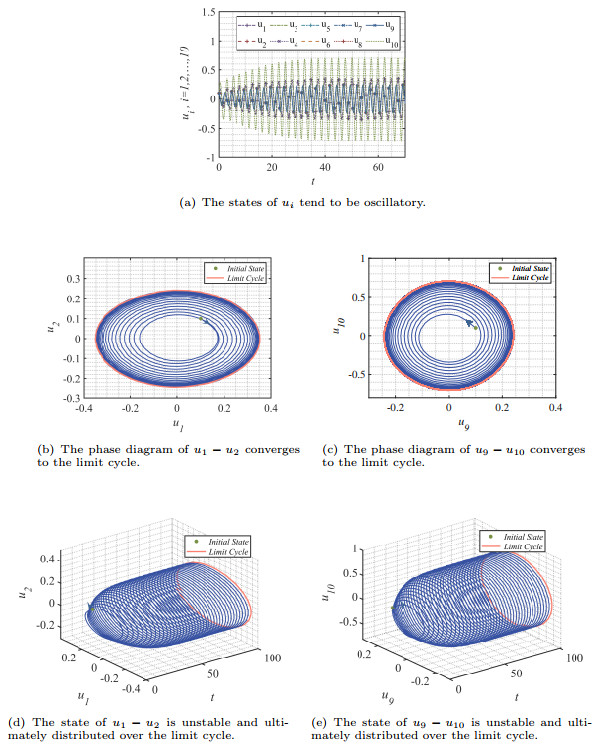
Figure 9.
The waveforms of network (4.2) with
$ \theta=4 $ $ E^* $ $ \tau \geq 0 $ -
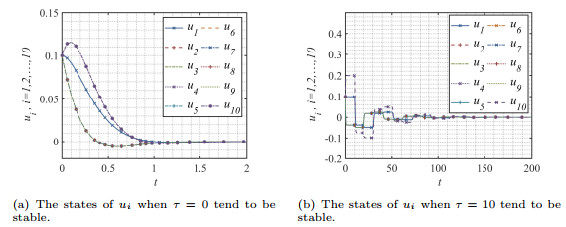
Figure 10.
The temporal evolutions of network (4.2) with
$ \theta = 1 $ $ \tau = 0.05 < \tau_0 = 0.137 $ $ E^* $ -
Figure 11.
The temporal evolutions of network (4.2) with
$ \theta = 1 $ $ \tau = 0.15 > \tau_0 = 0.137 $ $ E^* $ -
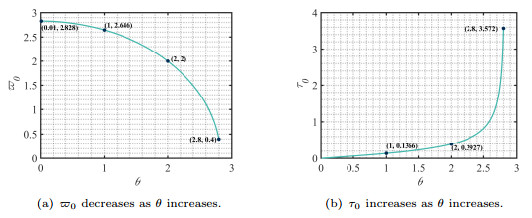
Figure 12.
The fluctuations of critical values
$ \varpi_0 $ $ \tau_0 $ $ \theta $ -
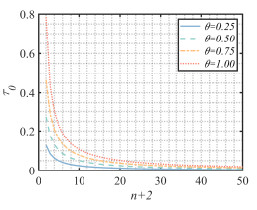
Figure 13.
The fluctuations of critical values
$ \tau_0 $ $ n+2 $ $ \theta $