| Citation: |
Ning Zhang, Haodong Wang, Wenxue Li. DUPIRE ITÔ'S FORMULA FOR THE EXPONENTIAL SYNCHRONIZATION OF STOCHASTIC SEMI-MARKOV JUMP SYSTEMS WITH MIXED DELAY UNDER IMPULSIVE CONTROL[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2082-2108. doi: 10.11948/20230195
|
DUPIRE ITÔ'S FORMULA FOR THE EXPONENTIAL SYNCHRONIZATION OF STOCHASTIC SEMI-MARKOV JUMP SYSTEMS WITH MIXED DELAY UNDER IMPULSIVE CONTROL
-
Abstract
This paper emphasizes the exponential synchronization for a class of stochastic semi-Markov jump systems with mixed delay via stochastic hybrid impulsive control. The impulsive sequence includes synchronous and asynchronous impulses with the impulsive gains being a sequence of stochastic variables. Inspired by the idea of average, a concept of "average stochastic impulsive gain" is used to qualify the impulse intensity. Our approach expands Dupire functional Itô's formula to the stochastic semi-Markov jump systems with mixed delay for the first time. Moreover, in view of the established Lyapunov functional, graph theory, and stochastic analysis theory, some exponential synchronization criteria for the systems are derived. The theoretical results are applied to a class of Chua's circuit systems with semi-Markov jump and mixed delay. Some synchronization criteria for the circuit systems are provided. The simulation results verify the effectiveness of the theoretical results.
-
-
References
[1] D. A. Burbano-L., S. Yaghouti, C. Petrarca, M. de Magistris and M. di Bernardo, Synchronization in multiplex networks of Chua's circuits: Theory and experiments, IEEE Transactions on Circuits and Systems Ⅰ-Regular Papers, 2020, 67(3), 927–938. doi: 10.1109/TCSI.2019.2955972 [2] J. Chen, Z. Zeng and P. Jiang, Global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks, Neural Networks, 2014, 51, 1–8. doi: 10.1016/j.neunet.2013.11.016 [3] T. Chen, X. Liu and Y. Wu, Prescribed-time stabilization of complex networks with intermittent control, IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2023. DOI: 10.1109/TCSII.2023.3330851. [4] V. K. R. Chimmula and L. Zhang, Time series forecasting of COVID-19 transmission in Canada using LSTM networks, Chaos Solitons & Fractals, 2020, 135, 109864. [5] S. V. Dhople, B. B. Johnson, F. Doerfler and A. O. Hamadeh, Synchronization of nonlinear circuits in dynamic electrical networks with general topologies, IEEE Transactions on Circuits and Systems Ⅰ-Regular Papers, 2014, 61(9), 2677–2690. doi: 10.1109/TCSI.2014.2332250 [6] S. Dong, G. Chen, M. Liu and Z. Wu, Robust adaptive H-infinity control for networked uncertain semi-Markov jump nonlinear systems with input quantization, Science China-Information Sciences, 2022, 65(8), 189201. doi: 10.1007/s11432-020-3187-8 [7] A. Doria-Cerezo, J. M. Olm, M. Di Bernardo and E. Nuno, Modelling and control for bounded synchronization in multi-terminal VSC-HVDC transmission networks, IEEE Transactions on Circuits and Systems Ⅰ-Regular Papers, 2016, 63(6), 916–925. doi: 10.1109/TCSI.2016.2537938 [8] N. Du, D. Nguyen, N. Nguyen and G. Yin, Stability of stochastic functional differential equations with random switching and applications, Automatica, 2021, 125, 109410. doi: 10.1016/j.automatica.2020.109410 [9] B. Dupire, Functional Ito calculus, Quantitative Finance, 2019, 19(5), 721–729. doi: 10.1080/14697688.2019.1575974 [10] X. Ge, Q. Han, L. Ding, Y. Wang and X. Zhang, Dynamic event-triggered distributed coordination control and its applications: A survey of trends and techniques, 2020, 50(9), 3112–3125. [11] N. Gunasekaran, G. Zhai and Q. Yu, Sampled-data synchronization of delayed multi-agent networks and its application to coupled circuit, Neurocomputing, 2020, 413, 499–511. doi: 10.1016/j.neucom.2020.05.060 [12] B. Guo, Y. Xiao, C. Zhang and Y. Zhao, Graph theory-based adaptive intermittent synchronization for stochastic delayed complex networks with semi-Markov jump, Applied Mathematics and Computation, 2020, 366, 124739. doi: 10.1016/j.amc.2019.124739 [13] W. Guo, Y. Zhang and W. Li, Synchronization for the coupled stochastic strict-feedback nonlinear systems with delays under pinning control, Nonlinear Analysis: Hybrid Systems, 2023, 48, 101326. doi: 10.1016/j.nahs.2022.101326 [14] Y. Guo and Y. Li, Bipartite leader-following synchronization of fractional-order delayed multilayer signed networks by adaptive and impulsive controllers, Applied Mathematics and Computation, 2022, 430, 127243. doi: 10.1016/j.amc.2022.127243 [15] S. Hu and Q. Zhu, Stochastic optimal control and analysis of stability of networked control systems with long delay, Automatica, 2003, 39(11), 1877–1884. doi: 10.1016/S0005-1098(03)00196-1 [16] X. Ji, J. Lu, B. Jiang and K. Shi, Distributed synchronization of delayed neural networks: Delay-dependent hybrid impulsive control, IEEE Transactions on Network Science and Engineering, 2022, 9(2), 634–647. doi: 10.1109/TNSE.2021.3128244 [17] T. Jia, X. Chen, F. Zhao, J. Cao and J. Qiu, Adaptive fixed-time synchronization of stochastic memristor-based neural networks with discontinuous activations and mixed delays, Journal of the Franklin Institute, 2023, 360(4), 3364–3388. doi: 10.1016/j.jfranklin.2022.11.006 [18] X. Jin, S. Wang, J. Qin, W. Zheng and Y. Kang, Adaptive fault-tolerant consensus for a class of uncertain nonlinear second-order multi-agent systems with circuit implementation, IEEE Transactions on Circuits and Systems Ⅰ-Regular Papers, 2018, 65(7), 2243–2255. doi: 10.1109/TCSI.2017.2782729 [19] J. Li, H. Jiang, J. Wang, C. Hu and G. Zhang, H infinity exponential synchronization of complex networks: aperiodic sampled-data-based event-triggered control, IEEE Transactions on Cybernetics, 2022, 52(8), 7968–7980. doi: 10.1109/TCYB.2021.3052098 [20] S. Li, Y. Zheng and H. Su, Almost sure synchronization of multilayer networks via intermittent pinning noises: A white-noise-based time-varying coupling, IEEE Transactions on Circuits and Systems Ⅰ-Regular Papers, 2021, 68(8), 3460–3473. doi: 10.1109/TCSI.2021.3082005 [21] X. Li and G. Yang, Graph theory-based pinning synchronization of stochastic complex dynamical networks, IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(2), 427–437. doi: 10.1109/TNNLS.2016.2515080 [22] H. Liu, F. Zhao, M. Wang, J. Qiu and X. Chen, Finite-time pinning impulsive synchronization of stochastic complex networks with mixed delays, Applied Mathematical Modelling, 2023, 117, 840–850. doi: 10.1016/j.apm.2023.01.023 [23] X. Liu, D. W. C. Ho, Q. Song and W. Xu, Finite/Fixed-time pinning synchronization of complex networks with stochastic disturbances, IEEE Transactions on Cybernetics, 2019, 49(6), 2398–2403. doi: 10.1109/TCYB.2018.2821119 [24] Y. Liu, J. Liu and W. Li, Stabilization of highly nonlinear stochastic coupled systems via periodically intermittent control, IEEE Transactions on Automatic Control, 2021, 66(10), 4799–4806. doi: 10.1109/TAC.2020.3036035 [25] Y. Liu, Z. Wang and X. Liu, Global exponential stability of generalized recurrent neural networks with discrete and distributed delays, Neural Networks, 2006, 19(5), 667–675. doi: 10.1016/j.neunet.2005.03.015 [26] J. Lu, D. W. C. Ho and J. Cao, A unified synchronization criterion for impulsive dynamical networks, Automatica, 2010, 46(7), 1215–1221. doi: 10.1016/j.automatica.2010.04.005 [27] D. Nesic and A. Teel, Input-output stability properties of networked control systems, IEEE Transactions on Automatic Control, 2004, 49(10), 1650–1667. doi: 10.1109/TAC.2004.835360 [28] D. Nguyen and G. Yin, Stability of stochastic functional differential equations with regime-switching: Analysis using Dupire's functional Ito formula, Potential Analysis, 2020, 53(1), 247–265. doi: 10.1007/s11118-019-09767-x [29] H. Shen, M. Chen, Z. Wu, J. Cao and J. Park, Reliable event-triggered asynchronous extended passive control for semi-Markov jump fuzzy systems and its application, IEEE Transactions on Fuzzy Systems, 2020, 28(8), 1708–1722. [30] H. Shen, F. Li, J. Cao, Z. Wu and G. Lu, Fuzzy-model-based output feedback reliable control for network-based semi-Markov jump nonlinear systems subject to redundant channels, IEEE Transactions on Cybernetics, 2020, 50(11), 4599–4609. doi: 10.1109/TCYB.2019.2959908 [31] X. Song, R. Zhang, C. Ahn and S. Song, Synchronization for semi-Markovian jumping reaction-diffusion complex dynamical networks: A space-time sampled-data control scheme, IEEE Transactions on Network Science and Engineering, 2022, 9(4), 2684–2696. doi: 10.1109/TNSE.2022.3168867 [32] J. Sun, M. Zang, P. Liu and Y. Wang, A secure communication scheme of three-variable chaotic coupling synchronization based on DNA chemical reaction networks, IEEE Transactions on Signal Processing, 2022, 70, 2362–2373. doi: 10.1109/TSP.2022.3173154 [33] Y. Tian, H. Yan, H. Zhang, J. Cheng and H. Shen, Asynchronous output feedback control of hidden semi-Markov jump systems with random mode-dependent delays, IEEE Transactions on Automatic Control, 2022, 67(8), 4107–4114. doi: 10.1109/TAC.2021.3110006 [34] H. Wang, S. Duan, T. Huang and J. Tan, Synchronization of memristive delayed neural networks via hybrid impulsive control, Neurocomputing, 2017, 267, 615–623. doi: 10.1016/j.neucom.2017.06.028 [35] N. Wang, X. Li, J. Lu and F. E. Alsaadi, Unified synchronization criteria in an array of coupled neural networks with hybrid impulses, Neural Networks, 2018, 101, 25–32. doi: 10.1016/j.neunet.2018.01.017 [36] P. Wang, B. Zhang and H. Su, Stabilization of stochastic uncertain complex-valued delayed networks via aperiodically intermittent nonlinear control, IEEE Transactions on Systems Man Cybernetics-Systems, 2019, 49(3), 649–662. doi: 10.1109/TSMC.2018.2818129 [37] Z. Wang, J. Cao, Z. Duan and X. Liu, Synchronization of coupled Duffing-type oscillator dynamical networks, Neurocomputing, 2014, 136, 162–169. doi: 10.1016/j.neucom.2014.01.016 [38] Y. Wu, Z. Sun, G. Ran and L. Xue, Intermittent control for fixed-time synchronization of coupled networks, IEEE/CAA Journal of Automatica Sinica, 2023, 10(6), 1488–1490. doi: 10.1109/JAS.2023.123363 [39] D. Xu, J. Pang and H. Su, Bipartite synchronization of signed networks via aperiodically intermittent control based on discrete-time state observations, Neural Networks, 2021, 144, 307–319. doi: 10.1016/j.neunet.2021.08.035 [40] Y. Xu, T. Lin, X. Liu and W. Li, Exponential bipartite synchronization of fractional-order multilayer signed networks via hybrid impulsive control, IEEE Transactions on Cybernetics, 2023, 53(6), 3926–3938. doi: 10.1109/TCYB.2022.3190413 [41] N. Yang, X. Gu and H. Su, Event-triggered delayed impulsive control for functional differential systems on networks, Communications in Nonlinear Science and Numerical Simulation, 2024. DOI: 10.1016/j.cnsns.2024.107850. [42] X. Yang, X. Li, J. Lu and Z. Cheng, Synchronization of time-delayed complex networks with switching topology via hybrid actuator fault and impulsive effects control, IEEE Transactions on Cybernetics, 2020, 50(9), 4043–4052. doi: 10.1109/TCYB.2019.2938217 [43] W. Yu, G. Chen and J. Cao, Adaptive synchronization of uncertain coupled stochastic complex networks, Asian Journal of Control, 2011, 13(3), 418–429. doi: 10.1002/asjc.180 [44] C. Zhang, W. Li and K. Wang, Exponential synchronization of stochastic coupled oscillators networks with delays, Applicable Analysis, 2017, 96(6), 1058–1075. doi: 10.1080/00036811.2016.1178240 [45] H. Zhang, Z. Qiu and L. Xiong, Stochastic stability criterion of neutral-type neural networks with additive time-varying delay and uncertain semi-Markov jump, Neurocomputing, 2019, 333, 395–406. doi: 10.1016/j.neucom.2018.12.028 [46] N. Zhang, X. Wang and W. Li, Stability for multi-linked stochastic delayed complex networks with stochastic hybrid impulses by Dupire Itô's formula, Nonlinear Analysis-Hybrid Systems, 2022, 45, 101200. doi: 10.1016/j.nahs.2022.101200 [47] N. Zhang, X. Wang, C. Tong and W. Li, Semi-global exponential stability of stochastic nonlinear functional sampling systems by emulation approach, Communications in Nonlinear Science and Numerical Simulation, 2023, 125(6), 107336. [48] W. Zhang, X. Yang and C. Li, Fixed-time stochastic synchronization of complex networks via continuous control, IEEE Transactions on Cybernetics, 2019, 49(8), 3099–3104. doi: 10.1109/TCYB.2018.2839109 [49] X. Zhao, L. Liu, H. Wang and M. Fan, Ecological effects of predator harvesting and environmental noises on oceanic coral reefs, Bulletin of Mathematical Biology, 2023, 85(7), 59. doi: 10.1007/s11538-023-01166-z [50] H. Zhou, S. Li and C. Zhang, Synchronization of hybrid switching diffusions delayed networks via stochastic event-triggered control, Neural Networks, 2023, 159, 1–13. doi: 10.1016/j.neunet.2022.11.034 -
-
Figures(8) / Tables(4)
Export File
Citation
Ning Zhang, Haodong Wang, Wenxue Li. DUPIRE ITÔ'S FORMULA FOR THE EXPONENTIAL SYNCHRONIZATION OF STOCHASTIC SEMI-MARKOV JUMP SYSTEMS WITH MIXED DELAY UNDER IMPULSIVE CONTROL[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 2082-2108. doi: 10.11948/20230195
Format
Content
DownLoad:
-
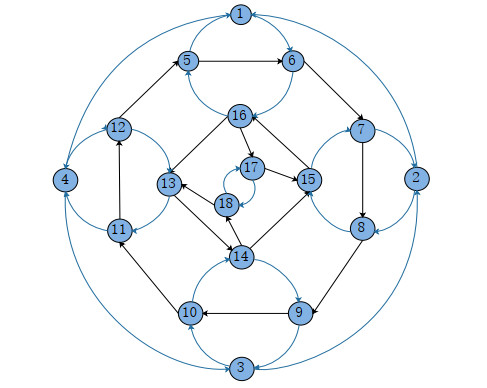
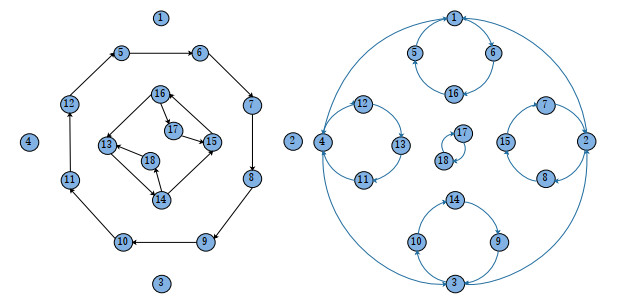
Figure 1.
Digraph
$ (G, \Pi^{1}) $ $ (G, \Pi^{2}) $ -
Figure 2.
Digraph
$ (G, THE) $ -
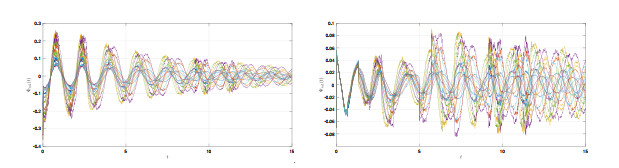
Figure 3.
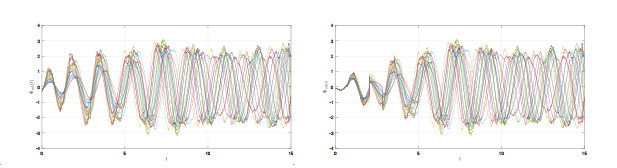
State trajectories
$ \Phi_{m1}(t) $ $ \Psi_{m1}(t) $ -
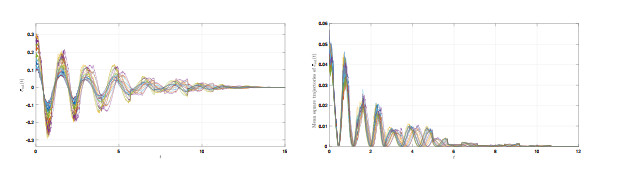
Figure 4.
State trajectories
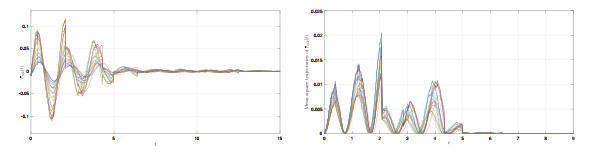
$ \bar{e}_{m1}(t) $ $ \mathbb{E}|\bar{e}_{m1}(t)|^{2} $ -
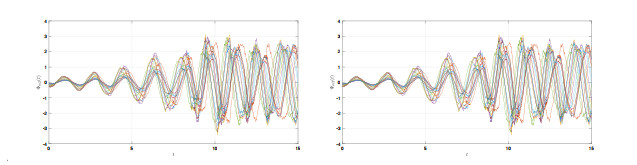
Figure 5.
State trajectories
$ \Phi_{m2}(t) $ $ \Psi_{m2}(t) $ -
Figure 6.
State trajectories
$ \bar{e}_{m2}(t) $ $ \mathbb{E}|\bar{e}_{m2}(t)|^{2} $ -
Figure 7.
State trajectories
$ \Phi_{m3}(t) $ $ \Psi_{m3}(t) $ -
Figure 8.
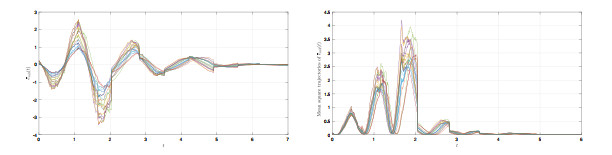
State trajectories
$ \bar{e}_{m3}(t) $ $ \mathbb{E}|\bar{e}_{m3}(t)|^{2} $