| Citation: |
Qian Hu, Zhihong Liu, Wei Jin, Wenbo Zhang. UNIVALENCE CONDITIONS AND RADIUS PROBLEMS FOR HARMONIC DIFFERENTIAL OPERATORS[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 947-963. doi: 10.11948/20230218
|
UNIVALENCE CONDITIONS AND RADIUS PROBLEMS FOR HARMONIC DIFFERENTIAL OPERATORS
-
Abstract
This article mainly studies univalence condition, the radius problem of fully starlike (fully convex) and uniformly starlike (uniformly convex) for the harmonic mapping differential operator under specific coefficient conditions. Firstly, several criteria for the univalence of harmonic differential operator terms are obtained, followed by the fully starlike and fully convex radius of the harmonic differential operator $D[f] \in \mathcal{K}_H^2(\lambda)$. Next, the radius of uniformly starlike and uniformly convex of the harmonic differential operator is obtained. Finally, the radius of uniformly starlike and uniformly convex of the harmonic mapping convolution differential operator is obtained.
-
-
References
[1] Z. Abdulhadi, Y. A. Muhanna and S. Khuri, On some properties of solutions of the biharmonic equation, Appl. Math. Comput., 2006, 177(1), 346-351. [2] J. W. Alexander, Functions which map the interior of the unit circle upon simple regions, Ann. Math., 1915, 17(1), 12-22. doi: 10.2307/2007212 [3] F. M. Al-Oboudi, On univalent functions defined by a generalized Sălăgean operator, Int. J. Math. Math. Sci., 2004, 2004(27), 1429-1436. doi: 10.1155/S0161171204108090 [4] F. G. Avkhadiev, R. G. Nasibullin and I. K. Shafigullin, Becker type univalence conditions for harmonic mappings, Russ. Math., 2016, 60, 69-73. [5] S. Beig and V. Ravichandran, Convolution and convex combination of harmonic mappings, Bull. Iran. Math. Soc., 2019, 45, 1467-1486. doi: 10.1007/s41980-019-00209-3 [6] J. E. Brown, Images of disks under convex and starlike functions, Math. Z., 1989, 202, 457-462. doi: 10.1007/BF01221584 [7] M. Chuaqui, P. Duren and B. Osgood, Curvature properties of planar harmonic mappings, Comput. Methods Funct. Theory, 2004, 4(1), 127-142. doi: 10.1007/BF03321060 [8] J. Clunie and T. Sheil-Small, Harmonic univalent functions, Ann. Acad. Sci. Fenn., 1984, 9, 3-25. doi: 10.5186/aasfm.1984.0905 [9] M. Dorff, M. Nowak and M. Wołoszkiewicz, Convolutions of harmonic convex mappings, Complex Var. Elliptic Equ., 2012, 57(5), 489-503. doi: 10.1080/17476933.2010.487211 [10] N. Ghosh and A. Vasudevarao, The radii of fully starlikeness and fully convexity of a harmonic operator, Monatsh. Math., 2019, 188, 653-666. doi: 10.1007/s00605-018-1163-1 [11] M. R. Goodloe, Hadamard products of convex harmonic mappings, Complex Var., 2002, 47(2), 81-92. [12] A. W. Goodman, On uniformly starlike functions, J. Math. Anal. Appl., 1991, 155(2), 364-370. doi: 10.1016/0022-247X(91)90006-L [13] J. M. Jahangiri, Harmonic functions starlike in the unit disk, J. Math. Anal. Appl., 1999, 235(2), 470-477. doi: 10.1006/jmaa.1999.6377 [14] D. Kalaj, S. Ponnusamy and M. Vuorinen, Radius of close-to-convexity and fully starlikeness of harmonic mappings, Complex Var. Elliptic Equ., 2014, 59(4), 539-552. doi: 10.1080/17476933.2012.759565 [15] H. Lewy, On the non-vanishing of the Jacobian in certain one-to-one mappings, Bull. Amer. Math. Soc., 1936, 42(10), 689-692. doi: 10.1090/S0002-9904-1936-06397-4 [16] L. L. Li and S. Ponnusamy, Note on the convolution of harmonic mappings, Bull. Aust. Math. Soc., 2019, 99(3), 421-431. doi: 10.1017/S0004972719000029 [17] Z. H. Liu and S. Ponnusamy, Radius of fully starlikeness and fully convexity of harmonic linear differential operator, Bull. Korean Math. Soc., 2018, 55(3), 819-835. [18] Y. A. Muhanna and S. Ponnusamy, Extreme points method and univalent harmonic mappings, Complex Analysis and Dynamical Systems IV. Am. Math. Soc., 2016, 667, 223-237. [19] S. Nagpal and V. Ravichandran, Fully starlike and fully convex harmonic mappings of order α, Ann. Polon. Math., 2013, 108(1), 85-107. doi: 10.4064/ap108-1-7 [20] S. Ponnusamy and A. S. Kaliraj, Univalent harmonic mappings convex in one direction, Anal. Math. Phys., 2014, 4, 221-236. doi: 10.1007/s13324-013-0066-5 [21] S. Ponnusamy, H. Yamamoto and H. Yanagihara, Variability regions for certain families of harmonic univalent mappings, Complex Var. Elliptic Equ., 2013, 58(1), 23-34. doi: 10.1080/17476933.2010.551200 [22] P. T. Reddy, B. Venkateswarlu and S. Sreelakshmi, On the univalence criteria for analytic functions defined by differential operator, Int. J. Open Probl. Complex Anal., 2020, 12(1), 2074-2827. [23] T. Sheil-Small, Constants for planar harmonic mappings, J. Lond. Math. Soc., 1990, 2(2), 237-248. [24] X. T. Wang, X. Q. Liang and Y. L. Zhang, Precise coefficient estimates for close-to-convex harmonic univalent mappings, J. Math. Anal. Appl., 2001, 263(2), 501-509. doi: 10.1006/jmaa.2001.7626 -
-
Figures(1)
Export File
Citation
Qian Hu, Zhihong Liu, Wei Jin, Wenbo Zhang. UNIVALENCE CONDITIONS AND RADIUS PROBLEMS FOR HARMONIC DIFFERENTIAL OPERATORS[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 947-963. doi: 10.11948/20230218
Format
Content
DownLoad:
-
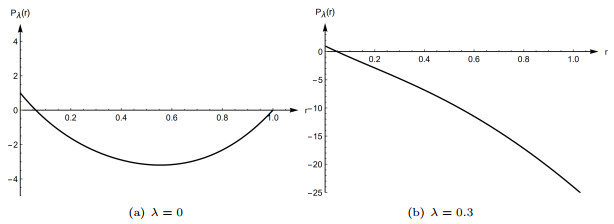
Figure 1.
The root of
$ P_{\lambda}(r) $