| Citation: | Junping Nan, Weimin Hu, You-Hui Su, Yongzhen Yun. EXISTENCE AND STABILITY OF SOLUTIONS FOR A COUPLED HADAMARD TYPE SEQUENCE FRACTIONAL DIFFERENTIAL SYSTEM ON GLUCOSE GRAPHS[J]. Journal of Applied Analysis & Computation, 2024, 14(2): 911-946. doi: 10.11948/20230202 |
EXISTENCE AND STABILITY OF SOLUTIONS FOR A COUPLED HADAMARD TYPE SEQUENCE FRACTIONAL DIFFERENTIAL SYSTEM ON GLUCOSE GRAPHS
-
Abstract
Chemical graph theory is an interdisciplinary mathematics and chemistry discipline that obtains mathematical information about the structure of target compounds and is an important research branch in theoretical pharmacology and nanomedicine. This paper study a coupled Hadamard type sequential fractional differential system on glucose graphs and establishes the Ulam's stability and existence of the system solutions. Furthermore, we examine examples against different background graphs and provide approximate graphs of the solutions. The novelty of this paper is that the origin of each edge is not fixed in modeling the glucose graphs, and one of the two vertices of the corresponding edge can be arbitrarily chosen as the origin to build the system and give the approximate graphs of the solutions using iterative methods and numerical simulation.
-

-
References
[1] A. Z. Abdian, A. Behmaram and G. H. Fath-Tabar, Graphs determined by signless Laplacian spectra, Akce. Int. J. Graphs. Co., 2020, 17(1), 45-50. doi: 10.1016/j.akcej.2018.06.009 [2] B. Ahmad, M. Alghanmi, A. Alsaedi, et al., Existence and uniqueness results for a nonlinear coupled system involving Caputo fractional derivatives with a new kind of coupled boundary conditions, Appl. Math. Lett., 2021, 116, 107018. doi: 10.1016/j.aml.2021.107018 [3] B. Ahmad, A. Alsaedi, S. K. Ntouyas, et al., Hadamard-Type Fractional Differential Equations, Inclusions and Inequalities, Cham, Switzerland, Springer, 2017. [4] A. Boroomand and M. B. Menhaj, Fractional-order hopfeld neural networks, Lect. Notes. Comput. Sc., 2009, 5509, 883-890. [5] L. Debnath, Fractional integrals and fractional differential equations in fluid mechanics, Frac. Calc. Appl. Anal., 2003, 6, 119155. [6] A. Din, Y. J. Li and A. Yusuf, Delayed hepatitis B epidemic model with stochastic analysis, Chao. Soliton. Fract., 2021, 146(1), 110839. [7] R. George, M. Houas, M. Ghaderi, et al., On a coupled system of pantograph problem with three sequential fractional derivatives by using positive contraction-type inequalities, Results Phys., 2022, 39, 105687. doi: 10.1016/j.rinp.2022.105687 [8] B. Ghanbari, On approximate solutions for a fractional prey-predator model involving the Atangana-Baleanu derivative, Adv. Differ. Equ-Ny., 2020, 1, 679. [9] D. G. Gordeziani, M. Kupreishvli, H. V. Meladze, et al., On the solution of boundary value problem for differential equations given in graphs, Appl. Math. Lett., 2008, 13, 80-91. [10] J. R. Graef, L. J. Kong and M. Wang, Existence and uniqueness of solutions for a fractional boundary value problem on a graph, Fract. Calc. Appl. Anal., 2014, 17, 499-510. doi: 10.2478/s13540-014-0182-4 [11] Z. J. Han and E. Zuazua, Decay rates for elastic-thermoelastic star-shaped networks, Netw. Heterog. Media., 2017, 12(3), 461-488. doi: 10.3934/nhm.2017020 [12] A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Amsterdam, Elsevier, 2006. [13] J. Klafter, S. C. Lim and R. Metzler, Fractional Dynamics in Physics, Singapore, World Scientific, 2011. [14] M. A. Krasnoselskii, Two remarks on the method of successive approximations, Uspekhi. Mat. Nauk., 1955, 10, 123-127. [15] C. S. Liu, E. R. El-Zahar and C. W. Chang, A boundary shape function iterative method for solving nonlinear singular boundary value problems, Math. Comput. Simul., 2021, 187, 614-629. doi: 10.1016/j.matcom.2021.03.030 [16] G. Lumer, Connecting of local operators and evolution equations on a network, Lect. Notes. Math., 1980, 787, 219-234. [17] A. Mahdy, M. S. Mohamed, K. A. Gepreel, et al., Dynamical characteristics and signal flow graph of nonlinear fractional smoking mathematical model, Chaos Soliton. Fract., 2020, 141, 110308. doi: 10.1016/j.chaos.2020.110308 [18] V. Mehandiratta, M. Mehra and G. Leugering, Existence and uniqueness results for a nonlinear Caputo fractional boundary value problem on a star graphs, J. Math. Anal. Appl., 2019, 477(2), 1243-1264. doi: 10.1016/j.jmaa.2019.05.011 [19] R. Metzler and J. Klafter, Boundary value problems for fractional diffusion equations, Phys A., 2000, 278(1-2), 107-125. doi: 10.1016/S0378-4371(99)00503-8 [20] S. Nicaise, Some results on spectral theory over networks applied to nerve impulse transmission, Lect. Notes. Math., 1985, 1771, 532-541. [21] V. Pivovarchik, Inverse problem for the Sturm-Liouville equation on a star-shaped graph, Math. Nachr., 2007, 280(13), 1595-1619. [22] M. Ruziev, A boundary value problem for a partial differential equation with fractional derivative, Fract. Cacl. Appl., 2021, 24(2), 509-517. doi: 10.1515/fca-2021-0022 [23] D. L. Shah and M. Alam, Hyers-Ulam stability of coupled implicit fractional integro-differential equations with Riemann-Liouville derivatives, Chaos. Soliton. Fract., 2021, 150, 111122. doi: 10.1016/j.chaos.2021.111122 [24] N. A. Sheikh, M. Jamil, D. Ching, et al., A generalized model for quantitative analysis of sediments loss: A Caputo time fractional model, J. King Saud. Univ. Sci., 2020, 33(1), 101179. [25] R. Subashini, K. Jothimani, K. S. Nisar, et al., New results on nonlocal functional integro-differential equations via Hilfer fractional derivative, Alex. Eng. J., 2020, 59(5), 2891-2899. doi: 10.1016/j.aej.2020.01.055 [26] A. N. Sultan, Nonlinear convolution integro-differential equation with variable coefficient, Fract. Cacl. Appl., 2021, 24(3), 848-864. doi: 10.1515/fca-2021-0036 [27] A. Sun, Y. H. Su and J. P. Sun, Existence of solutions to a class of fractional differential equations, J. Nonlinear. Model. Anal., 2022, 4, 409-442. [28] A. Sun, Y. H. Su, Q. C. Yuan, et. al., Existence of solutions to fractional differential equations with fractional-order derivative terms, J. Appl. Anal. Comput., 2021, 11, 486-520. [29] W. C. Sun, Y. H. Su and X. L. Han, Existence of solutions for a coupled system of caputo-hadamard fractional differential equations with p-laplacian operator, J. Appl. Anal. Comput, 2022, 12, 1885-1900. [30] W. C. Sun, Y. H. Su, A. Sun, et. al., Existence and simulation of positive solutions for m-point fractional differential equations with derivative terms, Open. Math., 2021, 19, 1820-1846. doi: 10.1515/math-2021-0131 [31] J. Tariboon, S. K. Ntouyas, S. Asawasamrit, et al., Positive solutions for Hadamard differential systems with fractional integral conditions on an unbounded domain, Open Math., 2017, 15(1), 645-666. doi: 10.1515/math-2017-0057 [32] D. Tripathil, S. Pandey and S. Das, Peristaltic flow of viscoelastic fluid with fractional maxwell model through a channel, Appl. Math. Comput., 2010, 215, 3645-3654. [33] A. Turab and W. Sintunavarat, The novel existence results of solutions for a nonlinear fractional boundary value problem on the ethane graph, Alex. Eng. J., 2021, 60(6), 5365-5374. doi: 10.1016/j.aej.2021.04.020 [34] J. R. Wang, Y. Zhou and M. Medve, Existence and stability of fractional differential equations with Hadamard derivative, Topol. Method Nonl. An., 2013, 41(1), 113-133. [35] S. H. Wang and Z. Zhou, Three solutions for a partial discrete Dirichlet boundary value problem with p-Laplacian, Bound. Value. Probl., 2021, 2021(1), 39. doi: 10.1186/s13661-021-01514-9 [36] T. Yu, L. Zhang, Y. D. Ji, et al., Stochastic resonance of two coupled fractional harmonic oscillators with fluctuating mass, Commun. Nonlinear. Sci., 2019, 72, 26-38. doi: 10.1016/j.cnsns.2018.11.009 [37] M. G. Zavgorodnii and Y. V. Pokornyi, On the spectrum of second-order boundary value problems on spatial networks, Usp. Mat. Nauk., 1989, 44, 220-221. [38] B. L. Zhang, V. D. Rdulescu and L. Wang, Existence results for Kirchhoff-type superlinear problems involving the fractional Laplacian, P. Roy. Soc. Edinb. A., 2018, 149(4), 1061-1081. [39] H. Y. Zhang, J. J. Ao and D. Mu, Eigenvalues of discontinuous third-order boundary value problems with eigenparameter-dependent boundary conditions, J. Math. Anal. Appl., 2021, 506(2), 125680. [40] W. Zhang and W. Liu, Existence and Ulam's type stability results for a class of fractional boundary value problems on a star graphs, Math. Method Appl. Sci., 2020, 43, 8568-8594. doi: 10.1002/mma.6516 -
-
-
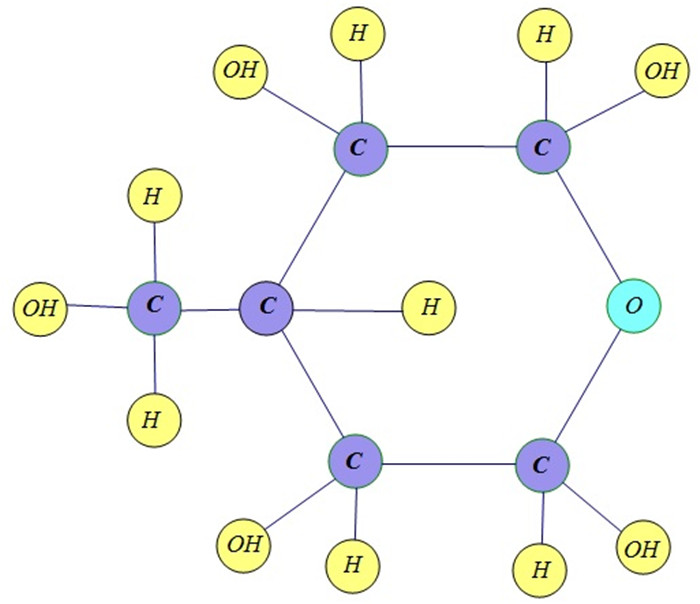
Figure 1.
Molecular structure of glucose.
-
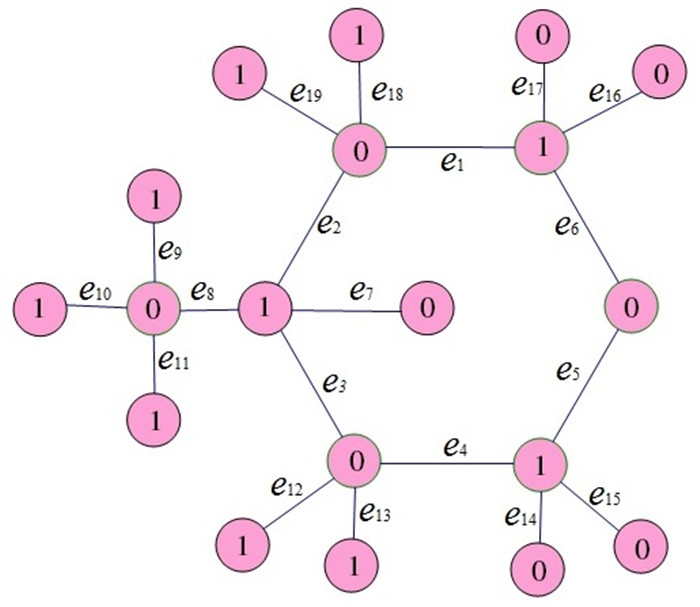
Figure 2.
Glucose graphs with vertices 0 or 1.
-
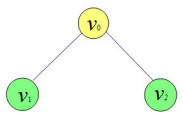
Figure 3.
A sketch of the star graphs
-
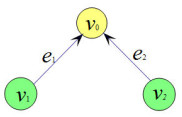
Figure 4.
A sketch of the directed star graphs
-
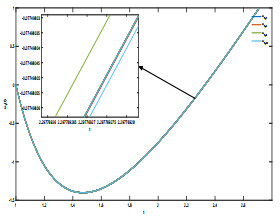
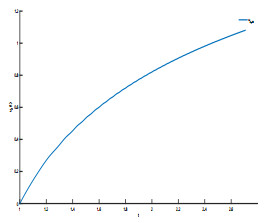
Figure 5.
Iterative process of u1
-
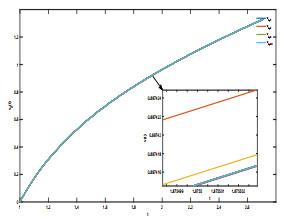
Figure 6.
Approximate solution of u1
-
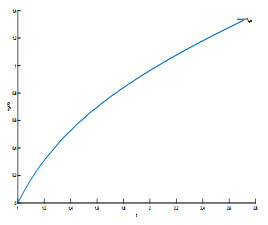
Figure 7.
Iterative process of v1
-
Figure 8.
Approximate solution of v1
-
Figure 9.
Iterative process of u2
-
Figure 10.
Approximate solution of u2
-
Figure 11.
Iterative process of v2
-
Figure 12.
Approximate solution of v2




 DownLoad:
DownLoad: